逻辑回归（Logistic Regression）是一种用于分类问题的统计方法，适用于二分类问题。其核心是通过Sigmoid 函数将线性回归的结果映射到概率区间 [0,1]，通常用于预测某事件是否发生。逻辑回归通过最小化对数损失函数（Log-Loss）来训练模型。它简单、易理解，适合线性可分的任务。

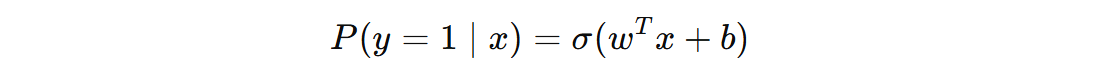
其中，w 是模型的权重向量，b 是偏置项，σ(z) 是 Sigmoid 函数。

1. 损失函数

我们使用最大似然估计来估计模型的参数 \( w \) 和 \( b \)。对于一个训练集，似然函数是每个样本的条件概率的乘积。

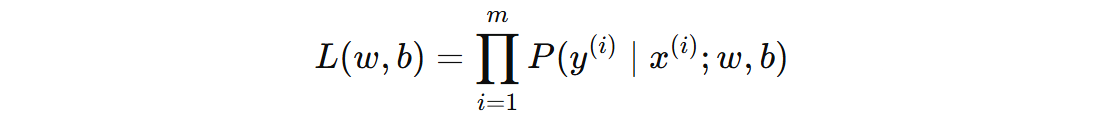
上面的公式展开如下（y 为 0 或者 1）：

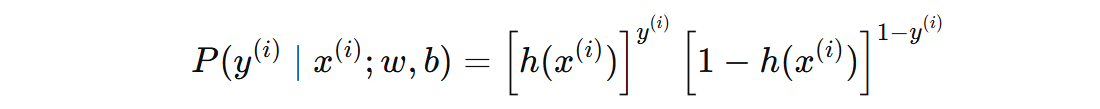
因此，整个训练集的似然函数是：

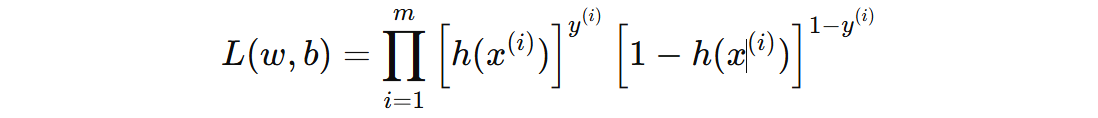
为了简化计算，我们对上面的似然函数取对数，得到对数似然函数（log-likelihood）：

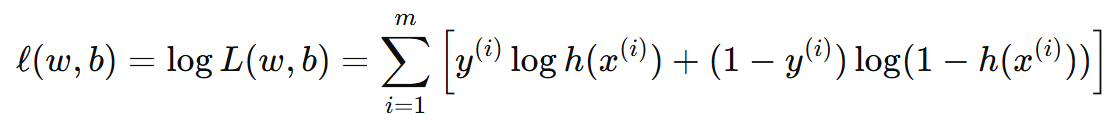
这个对数似然函数就是我们要最大化的目标函数。我们最终要 最小化 损失函数（即负对数似然），所以我们取对数似然函数的负数，得到 负对数似然损失函数（Negative Log-Likelihood Loss），也就是我们常说的逻辑回归的损失函数为：

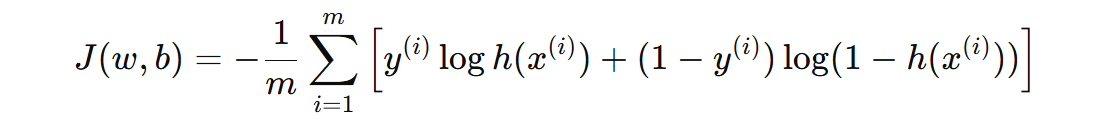
2. 参数学习

为了找到最优的 \( w \) 和 \( b \)，我们对对数似然函数进行梯度下降。对于每个参数 \( w_{j} \)​ 和偏置 \( b \)，我们计算梯度并更新参数。

对 \( w_{j} \)​​ 的梯度公式：

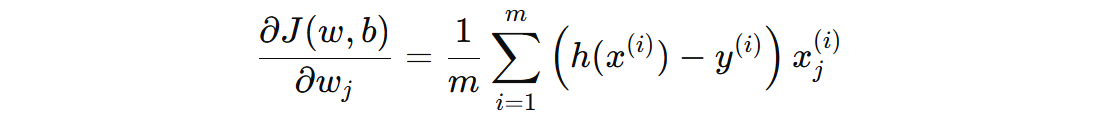
对 \( b \) 的梯度公式：

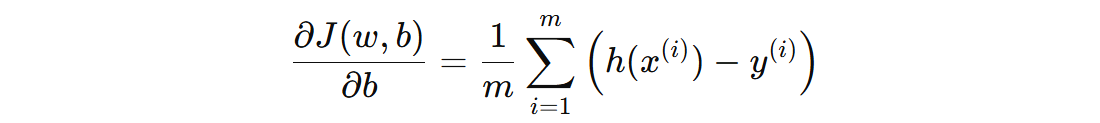
使用梯度下降法来更新参数 \( w_{j} \)​ 和偏置 \( b \)：

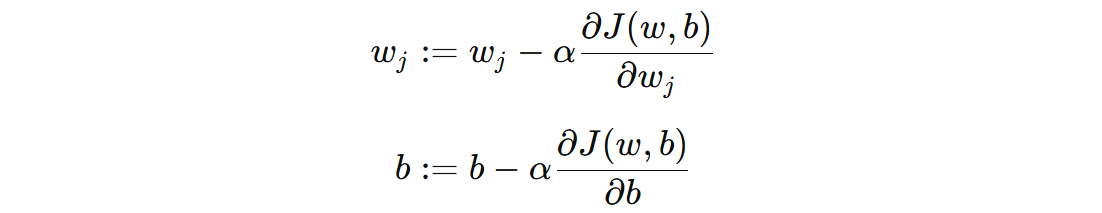
3. 算法实现

from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
import numpy as np
from sklearn.metrics import accuracy_score
import matplotlib.pyplot as plt


class MyLogisticRegression:

    def __init__(self):
        # 初始化参数
        self.w = np.ones(shape=(30,))
        self.b = 0

    def decision_function(self, x):
        z = x @ self.w + self.b
        return 1 / (1 + np.exp(-z))

    def predict(self, x):
        y_pred = self.decision_function(x)
        return np.where(y_pred > 0.5, 1, 0)

    def loss_function(self, x, y):
        y_pred = self.decision_function(x)
        y_pred = np.clip(y_pred, 1e-15, 1 - 1e-15)
        loss = -np.mean(np.log(y_pred) * y + np.log(1 - y_pred) * (1 - y))
        return loss

    def fit(self, x, y):

        alpha = 0.01
        train_loss = []
        for _ in range(1000):
            # 计算输出
            y_pred = self.decision_function(x)
            # 计算梯度
            w_grad = np.sum(x * (y_pred - y).reshape(-1, 1), axis=0) / x.shape[0]
            b_grad = np.sum(y_pred - y, axis=0) / x.shape[0]

            # 参数更新
            self.w = self.w - alpha * w_grad
            self.b = self.b - alpha * b_grad

            # 计算损失
            loss = self.loss_function(x, y)
            train_loss.append(loss)

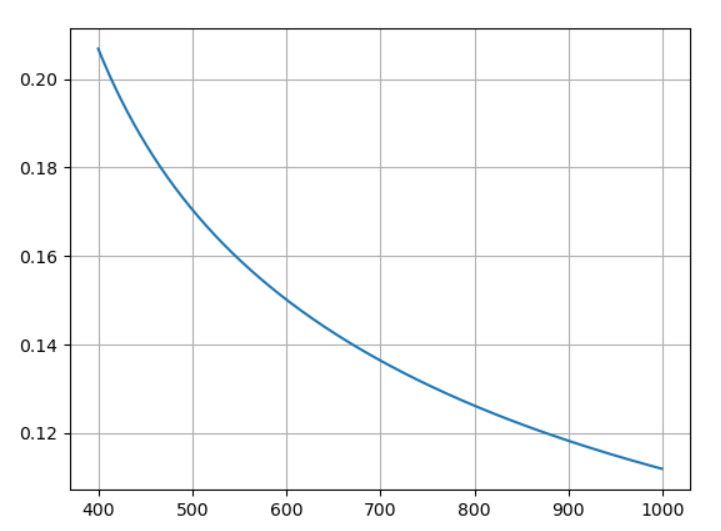
        x = range(len(train_loss))[400:]
        y = train_loss[400:]
        plt.plot(x, y)
        plt.grid()
        plt.show()


def test():
    data = load_breast_cancer()

    # 数据标准化
    scaler = StandardScaler()
    data.data = scaler.fit_transform(data.data)

    # 数据分割
    X_train, X_test, y_train, y_test = train_test_split(data.data, data.target, test_size=0.2, stratify=data.target, random_state=42)

    # 算法训练
    lr = MyLogisticRegression()
    lr.fit(X_train, y_train)

    # 算法评估
    y_pred = lr.predict(X_test)
    acc = accuracy_score(y_test, y_pred)
    print('Acc:', acc)


if __name__ == '__main__':
    test()

Acc: 0.930