1. SVM 目标函数

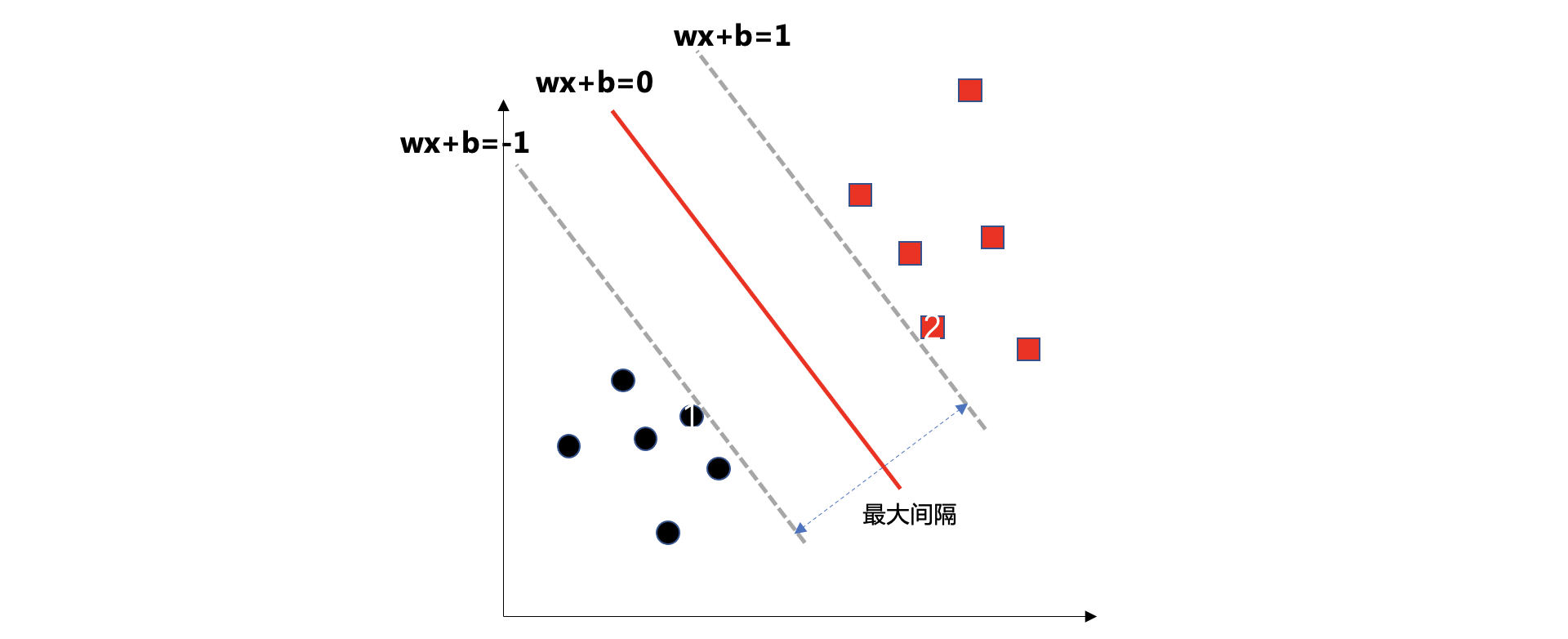
支持向量机的求解目标是：训练时，在能够将所有样本正确分类的前提下，追求间隔最大化。

如何表示最大间隔？我们把两条边界的直线用如下公式表示：

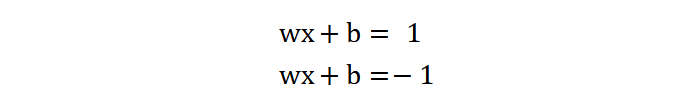
那我们要求解的支持向量机就可以表示为：

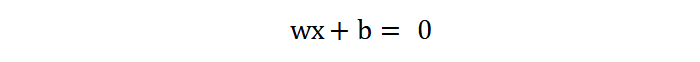
当 wx + b 小于 0 时，样本就会被预测为 -1 类别，否则就会被预测为 1 类别。落在 wx +b = 0 这条直线上的任何一点 \((x_{1}, x_{2})\)到 wx +b = 1 或 wx +b = -1 的距离公式为：

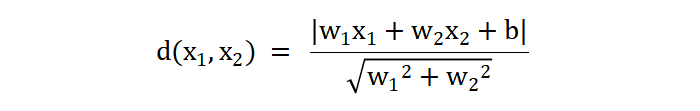
所以，两条边界线之间的最大间隔就可以表示为（即：当 w 和 b 参数为什么值时，能够使得间隔最大）：

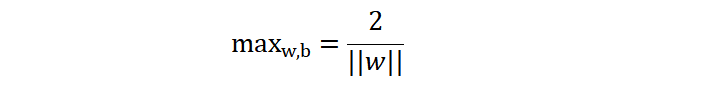
我们前面提到，最大间隔的前提是：样本分类正确，这个条件如何表示，如下：

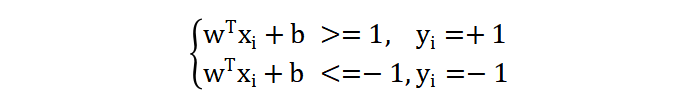
当样本的标签为 +1 时，那么 wx + b 值大于等于 1，当 样本的标签为 -1 时，那么 wx + b 的值小于 -1。接下来，我们将两个公式放在一起表示为：

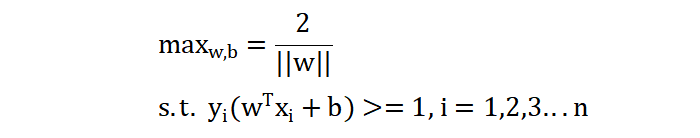
上面的优化目标是最大化问题，现在我们将其转换为最小化问题，如下：

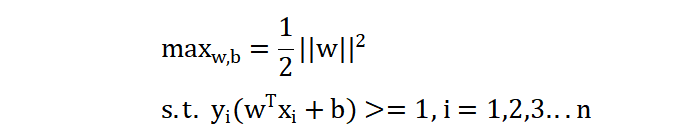
至此，线性可分支持向量机的目标函数已经确定，我们的目标就是求解其两个参数 w 和 b。

2. 目标问题转换

我们发现优化目标是一个带有约束条件的，不太容易求解。所以需要使用拉格朗日乘子法带有约束条件的问题，转换为不带约束条件的多元极值问题。朗格朗日问题的一般形式为：

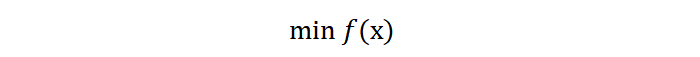
f(x) 是目标函数(最小化函数)，x 是问题的优化变量，且 x 必须满足一组约束条件。不等式的约束条件表示如下：

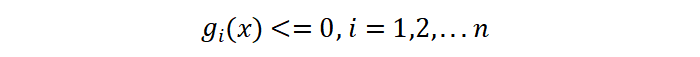
上面公式中 \(g_{i}(x)\) 是不等式约束条件。拉格朗日乘子法的基本思想是引入拉格朗日乘子将优化目标和条件合并到一起表示：

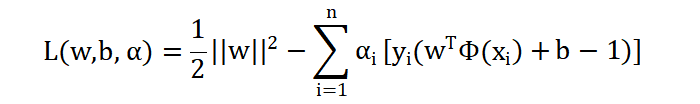
注意：原问题有两个求解的参数 w 和 b，现在多个 n 个 \(α_{i}\) 参数，现在问题变成如下表示：

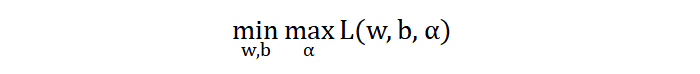
3. 对偶问题转换

支持向量机的优化目标是求解 w, b 为什么值时，整体的公式的值最小。而该问题又嵌套了一个内层关于 α 的问题，即：当 α 为什么值时，整体的公式的值最大，即：希望更多的样本分类正确。

即：SVM 目标函数最小化是一个嵌套的优化问题，其中内层问题涉及拉格朗日乘子法中的问题，而外层问题是原始问题，最终的目标是找到最佳的超平面以实现最大间隔分类。

对 w 和 b 求偏导，并令导数等于 0，得到如下结果：

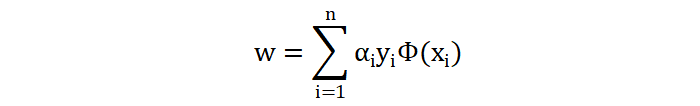
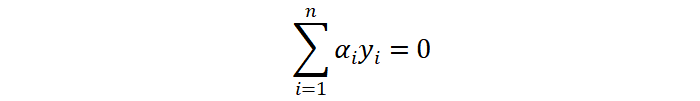
将对 w、b 求偏导的结果带入到原拉格朗日公式中，得到如下公式：

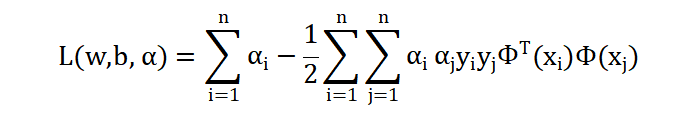
上述公式中，\(φ(x_{i})φ(x_{j})\) 表示两个向量在高维空间中的相似度。对于 α 的约束条件为：

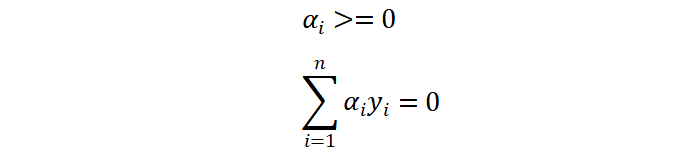
上面得到的公式是关于 α 的函数，即：求解当 α 为什么值时，上述公式的结果最大。

4. 决策函数

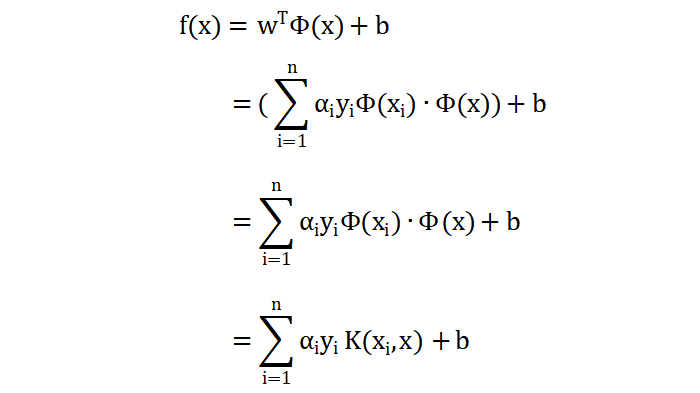
α 和偏置 b 的值可以通过对下面的问题求解获得：

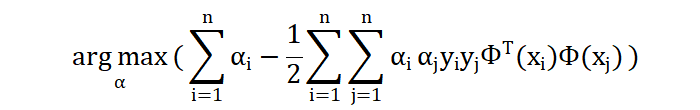
将上面的问题转换为极小值问题：

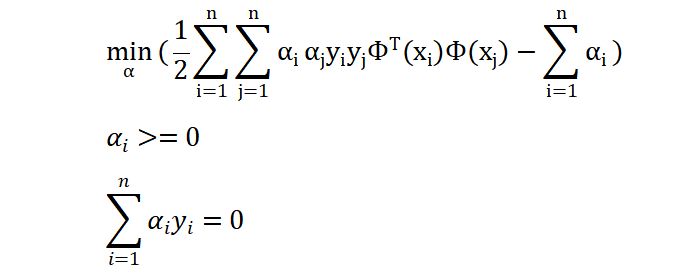
将训练样本代入上面公式，求解出 α 的值。然后将 α 值代入下面公式计算出 w, b 参数的值，注意：计算 b 时，可以选择支持向量（对应α 值不为0的样本，即：支持向量）中的任何一个：

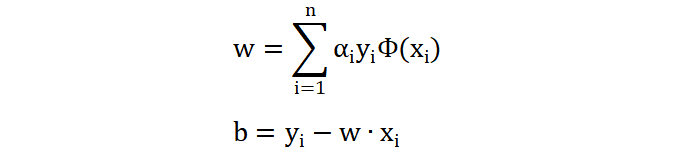
5. 计算例子

假设，我们有训练样本如下：

x1 = (3, 3)，y1 = +1
x2 = (4, 3)，y2 = +1
x3 = (1, 1)，y3 = -1

将这 3 个样本带入上述公式，得到如下结果：

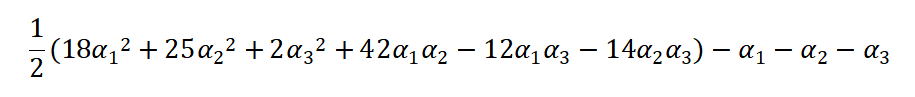
根据如下条件：

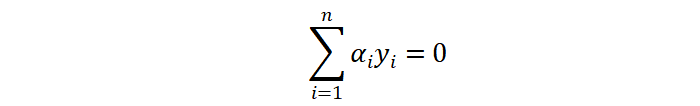
可得到：

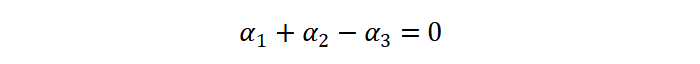
进而可得到：

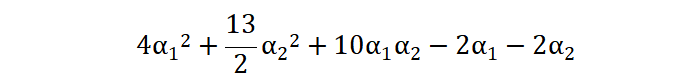
基于该公式对 \(α_{1}、α_{2}\) 求偏导，并令导数为0，可得 \(α_{1} = 1.5，α_{2} = -1\)。 由于条件限制中，α 的值必须大于等于0，故而正面的结果不是最终结果。我们在条件边界上寻找参数，即：

1. 当 \(α_{1} = 0\) 时，对 \(α_{2} \) 求偏导得出 \(α_{2} = 2/13, α_{3} = 2/13 \)
2. 当 \(α_{2} = 0\) 时，对 \(α_{2} \) 求偏导得出 \(α_{1} = 1/4, α_{3} = 1/4 \)

现在有两组结果，我们再看那组结果的值最小：

1. 第一组结果为：-0.1538
2. 第二组结果为：-0.25

显然第二组结果更小，所以 α 值为：

1. x1 样本对应的朗格朗日乘子为：\(α_{1} = 1/4 \)
2. x2 样本对应的朗格朗日乘子为：\(α_{2} = 0\)
3. x3 样本对应的朗格朗日乘子为：\(α_{3} = 1/4 \)

由如下公式：

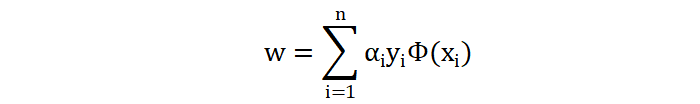
可得到 w = (0.5, 0.5)，再由如下公式：

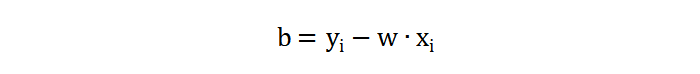
得到 b = -2，最终确定的 SVM 分类超平面为：

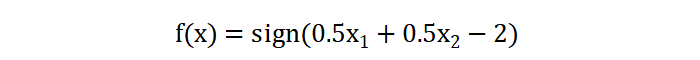
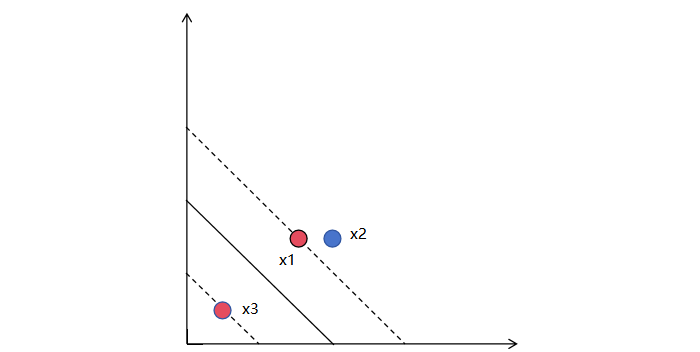
当我们拿到一个新的样本，代入到上面公式中，如果结果小于 0，则表示 -1 类，否则为 +1 类。