支持向量机高斯核函数（RBF）

支持向量机（SVM）强大的学习能力有很大程度上来源于高斯核函数的引入，并且 sklearn 中支持向量机默认的实现使用的就是高斯核函数。

我们看下支持向量机通过对偶问题转换后得到的数学表示：

http://mengbaoliang.cn/?p=13096

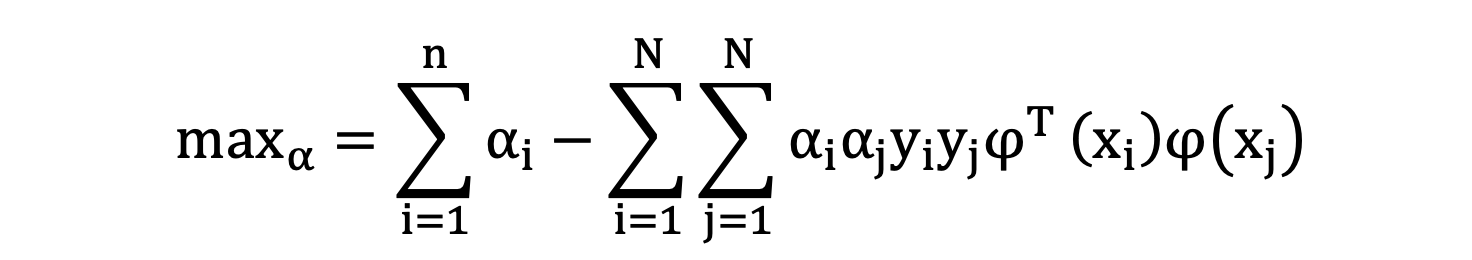
公式中，α 的值是每一个约束条件对优化目标的影响程度。α 的值大致分为两类，0 表示对寻找最大间隔没有影响，非0表示有影响。同时，我们也知道 α 非0值对应的样本就是支持向量，即：落在最大间隔边界上的样本。如下图中的 P 和 O 两个样本就是支持向量，其对应的 α 值不为 0，其他样本对应的 α 值都为 0.

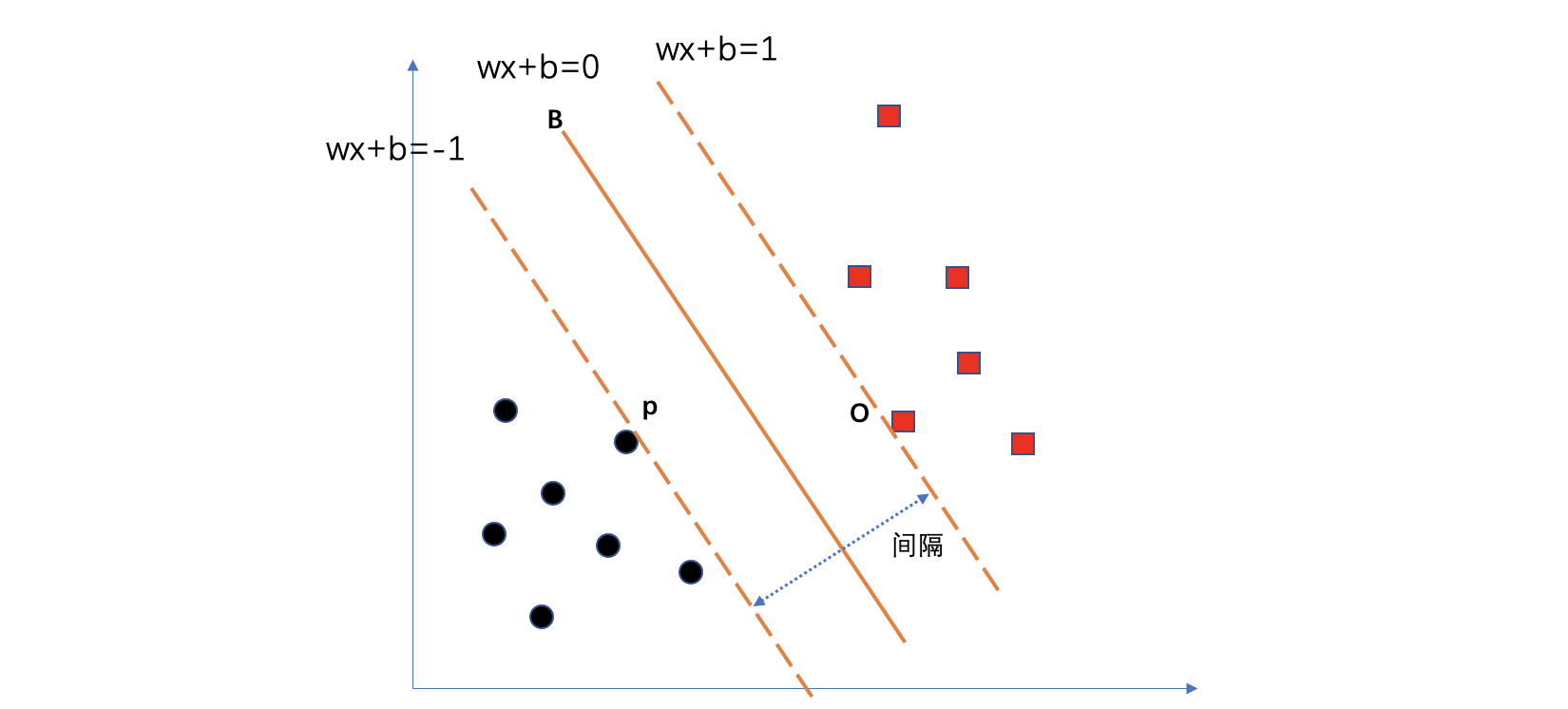
当我们知道 α 的值，确定了支持向量，就可以计算得到支持向量机参数的解。当然，上图的情况是线性可分的情况，实际上，我们拿到的训练数据大概率都是线性不可分的，也就是说，正负样本的分布存在相互重叠的现象。此时，把硬间隔（在线性可分条件下，间隔最大化）的条件换成软间隔，即：允许部分样本分错，换来较大的间隔。

另外的话，我们也可以通过改变正负样本的分布，然后在新的分布中，寻找线性可分、或者更少的训练样本错误率，并且获得一个较大的间隔，从而提升模型的学习效果。如果从这个角度来理解的话，我们就可以把支持向量机中的各种核函数理解为改变数据分布的函数。

比如说，多项式核函数，通过给数据增加组合特征，这就会使训练数据的分布发生变化。同理，高斯核函数也可以理解为改变样本的分布。

当然，我们可以把这个改变分布的行为通俗理解为，将原始数据投射到了另外一个空间中，这个空间是什么维度的，投射之后的向量具体表示是什么，我们是不知道的，只能理解为很高维度的空间。然后，在这个新的分布空间中寻找最优的分类超平面。

既然训练时，将数据投射到了一个更高维的空间中，所以，推理时也需要将新输入的样本进行投射到同样的空间中来判定预测结果。

回到我们要理解的高斯核函数上面来，从上面的 Paper 中，我们可以看到高斯核函数的数学表达式为：

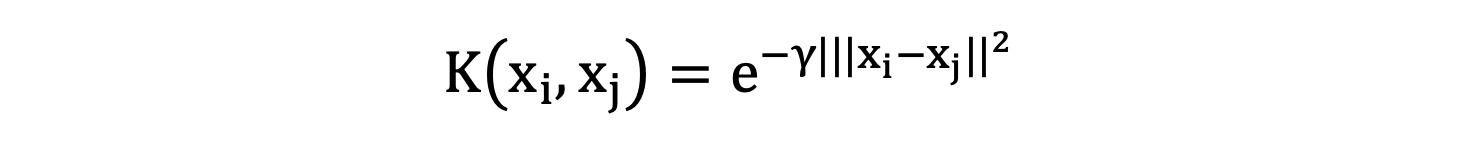
公式中 \(x_{i}\) 和 \(x_{j}\) 表示两个样本的向量表示。γ 为一个调节参数。

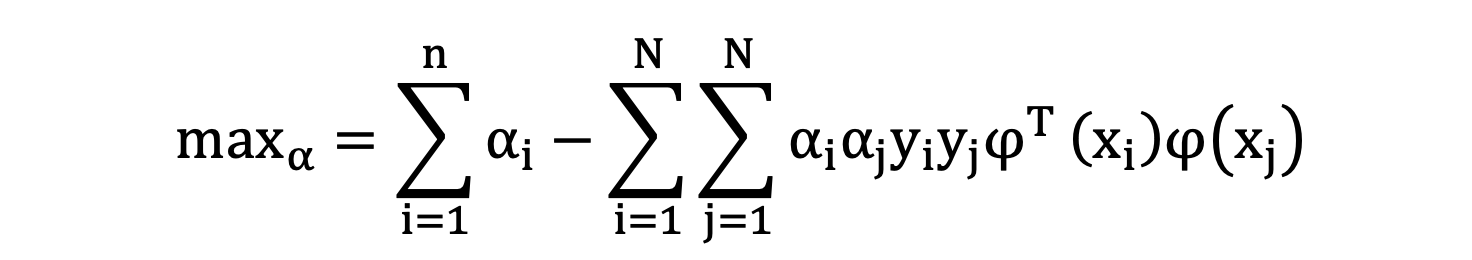
上面公式是由线性可分支持向量机推导而来的，假设训练集线性不可分，就可能导致我们无法得到 α 的解。当然引入软间隔，可以允许部分样本分类错误，从而得到一个 α 解，但是这就有可能导致训练集上的错误率较高，出现欠拟合的问题。所以，尝试通过对样本的分布进行变换，期望在一个新的分布中使得线性可分。

高斯核函数将每一个样本投射到更高维的空间中，然后计算点乘。至于投射之后的数据维度是多少、具体投射之后的向量的值是多少我不管，我就要求投射完成之后，我希望同类的样本尽可能的聚集、其他类的样本尽量远离，这个聚集的程度可以由 gamma 参数来调节。gamma 参数越大，则训练样本之间相似度越小，分布越分散，gamma 越小，则样本之间相似度越大，越聚集。如果训练样本都极端聚集到一起，此时我们将会很难寻找到合适的分类超平面。所以在什么样本的分布下能够找到合适的超平面，就需要调节该参数了。

加入了高斯核函数的支持向量机，分类边界可能就变成了曲面或者曲线，我觉得将数据投射到高维之后，多个支持向量构成了一个曲线的最大间隔边界。所以，引入了高斯核函数的支持向量机就应该是一个非线性的算法模型。

大体的话，有这么以下几点：

1. 我们可以在寻找超平面的时候的情况，分为线性可分、部分线性可分、近似完全不可分。对于线性可分的情况，我们直接使用硬间隔就可以拟合训练数据。如果是部分线性可分的情况，可以使用软间隔，允许分错部分样本。对于近似完全不可分的情况，软间隔可能会带来更高的训练数据的错误率，相当于训练出现欠拟合的问题，此时可使用核函数来改变数据的分布，在新的分布空间中去拟合训练数据。
2. 由于训练时改变了数据的分布，推理时，也需要将新的输入样本投射到训练时的数据分布中，再进行推理。以高斯核函数为例，新样本的投射计算过程需要用到支持向量，这也是为什么支持向量机是需要保存训练结果中得到的支持向量。
3. 对于经过对偶问题转换后的目标函数，点乘这部分其实就是在计算样本的相似程度。如果训练集数据中，样本都非常相似，意味着样本都聚集到了一起，使得无法寻找到合适的超平面。所以，通过核函数，将样本投射到新的空间中，在新的空间中，尽量让同类样本聚集，不同类样本分离，便于寻找超平面。这过程中还包含了 gamma 超参数，这个参数会影响到样本之间的相似程度。该值越大，计算得到的样本之间的距离就越大，样本之间就越分散，反之则训练样本就越聚集。太小的话，分类超平面就更复杂，容易过拟合。太大的话，分类超平面就过于简单，容易欠拟合。
4. 核函数的目的是为了改变数据分布，并且要求新的分布能够尽可能将正负样本分开。所以，我们并不需要了解究竟映射到了多少维度空间，以及在该空间中，向量的数值表示到底是什么。所以，核函数更像是定义投射之后的目标。
5. 将数据投射到新的分布空间之后，支持向量可能就会改变。例如：在原始空间中，AB两个样本作为支持向量，那么到了新的分布空间中，可能变成 DE 两个样本作为支持向量，并且对应的 α 值也会发生变化。
6. 多项式核函数本质也是改变数据的分布空间，或者也可以理解为将数据投射到高维空间。
7. 经过对偶问题转换的公式，目标是寻找支持向量。只要找到支持向量，就能够找到最大间隔的分类超平面。