在 Transformer 模型中,位置编码(Positional Encoding)是一种用来表示输入序列中每个 token 在序列中位置信息的技术。与 RNN 和 CNN 不同的是,Transformer 是基于自注意力机制的模型,而自注意力机制并不能捕捉输入 token 的位置关系,例如:输入序列中包含 \((x_1、x_2、x_3)\) 共 3 个 token, 对于 Transformer 而言 \(P(y|x_1,x_2,x_3)\) 和 \(P(y|x_2,x_3,x_1)\) 是一样的,可以理解为 基于自注意力机制的 Transformer 在建模时是忽略 token 的位置信息。
所以,为了能够在 Transformer 建模过程中,为 token 引入位置信息,提出了位置编码技术。这些方法主要包括两种方法:
- 绝对位置编码
- 相对位置编码
1. 绝对位置编码
绝对位置编码有两种方式,一种是可学习的绝对位置编码,一种的是固定的绝对位置编码。什么意思呢?Bert 模型使用的是第一种可学习的绝对位置编码,例如在 transformers 库中 Bert 的位置编码实现代码如下:
class BertEmbeddings(nn.Module):
"""Construct the embeddings from word, position and token_type embeddings."""
def __init__(self, config):
super().__init__()
self.word_embeddings = nn.Embedding(config.vocab_size, config.hidden_size, padding_idx=config.pad_token_id)
# 可学习的绝对位置编码
self.position_embeddings = nn.Embedding(config.max_position_embeddings, config.hidden_size)
self.token_type_embeddings = nn.Embedding(config.type_vocab_size, config.hidden_size)
我们可以看到这个绝对位置编码就是初始化了一个 Embedding 层,假设模型支持的最大输入长度为 512,编码维度为 768,则这个位置编码层的参数为: 12×768,每一行就是表示一个位置编码,模型反向传播时,来更新、学习位置编码。
另外一种方式就是固定的绝对位置编码,Transformer 原始论文中使用的是这种编码方式。它使用下面的公式来生成 512 个位置的编码表示,这个表示在模型训练过程中是固定不变的,不会随着反向传播而更新。

公式中的 pos 表示第 pos 个位置的编码,i 表示第 pos 个位置编码的第 i 个 维度的值。计算代码如下:
import torch
def test():
# 最大位置长度
max_pos = 8
d_model = 4
# 初始化位置编码
pos_embd = torch.zeros(max_len, d_model)
# 初始化位置索引
position = torch.arange(0, max_pos).reshape(-1, 1)
# 公式中的分子部分
div_term = 10000.0 ** (torch.arange(0, d_model, 2) / d_model )
pos_embd[:, 0::2] = torch.sin(position * div_term)
pos_embd[:, 1::2] = torch.cos(position * div_term)
print(pos_embd)
if __name__ == '__main__':
test()
程序输出结果:
tensor([[ 0.0000, 1.0000, 0.0000, 1.0000],
[ 0.8415, 0.5403, -0.5064, 0.8623],
[ 0.9093, -0.4161, -0.8733, 0.4872],
[ 0.1411, -0.9900, -0.9998, -0.0221],
[-0.7568, -0.6536, -0.8509, -0.5253],
[-0.9589, 0.2837, -0.4678, -0.8838],
[-0.2794, 0.9602, 0.0442, -0.9990],
[ 0.6570, 0.7539, 0.5440, -0.8391]])
2. 相对位置编码
相对位置编码是 Transformer 另外一种位置编码方式,绝对位置编码是为输入序列中的每个 token 引入了绝对位置信息,而相对位置编码则是引入了 token 之间的相对距离信息。
绝对位置编码一般都是在输入到编码器之前,加到 token 的 embedding 上,而相对位置编码则是在 self-attention 计算时引入。
例如:我们要进行 token A 对 token B 的 self-attention 计算,如果使用绝对位置编码的话,位置信息在送入编码器之前已经融入到两个 token 中了,此时直接可以进行 self-attention 计算。如果使用的是相对位置编码的话,此时就需要计算两个 token 之间的相对距离(A相对编码 – B相对编码),然后在 self-attention 计算时融入这一信息。
从这个过程,我们也可以看到了相对位置编码在使用时,需要每次动态计算,而绝对位置编码则不需要,性能上后者会好一些。
另外,相对位置编码是计算的两个 token 之间的相对距离,这个相对距离并不是无限大的,而是有个设定值。所以,这个设定值会影响到这个相对范围到底有多大。当两个 token 的相对距离超过了最大距离,那么会进行截断,也就是说,超过这个范围之后的相对位置编码是一样的表示。
相对位置编码另外一个优点,是能够适应更长的文本输入。例如:模型支持的最大长度是 128,如果我们输入的文本长度为 256,此时就不得不将其截断为两个 128 长度的 segment,此时如果使用绝对位置编码,我们会发现这两个 segment 第二个位置的编码是一样的,但是我们知道他们应该是不一样的。也就是说,绝对位置编码在同一个输入序列的多个 segment 中是不适合复用的。而相对位置编码由于关注的是相对距离,所以在同一个序列的两个 segment 中是可以复用的。
下面简单介绍下相对位置编码如何计算:
- 假设输入为:我是土生土长的中国人,我们要计算 “国” 对 “长” 的相对位置编码
- 首先计算下相对位置:”国” 的绝对位置 9,”长” 的绝对位置 6,相对位置为:9-6=3
- 初始化一个相对位置编码矩阵,假设我们关注的最大相对距离是 128,也就是说,对于一个 token 我们最多能关注到左右各 128 个的相对距离信息。并且每一个编码的维度是 32,则该矩阵大小为:(2 * 128 + 1, 32) = (257, 32),注意相对位置是两个方向,所以其实范围应该是 (-128, 128),这里统一表示到正数范围(0,257)
- 现在从这个相对位置编码矩阵中获得对应的编码:3+128=131,即这个矩阵的第 131 行为相对位置编码
- 相对位置编码也是一个可学习的,所以,我们需要初始化一个参数 P,使用这个参数对得到的相对位置编码进行变换就得到了最终想要的相对位置编码
最后,将相对位置编码应用到 self-attention 计算中即可,反向传播时会去更新、学习 P 参数,从而使得模型学习到了 token 之间的相对位置信息。
上面过程中,提到的相对位置编码矩阵也可以用前面提到的正弦+余弦的固定方式初始化,还是搞个可学习的都是可以的。
不同模型在使用相对位置编码计算 self-attention 时,可能会将相对位置编码应用到不同的公式中参与运算。
3. 《Self-Attention with Relative Position Representations》
Paper:https://arxiv.org/pdf/1803.02155.pdf
我们看看在这篇 Paper 中相对位置位置编码计算是如何应用到 self-attention 中,先看下 self-attention 的计算公式:
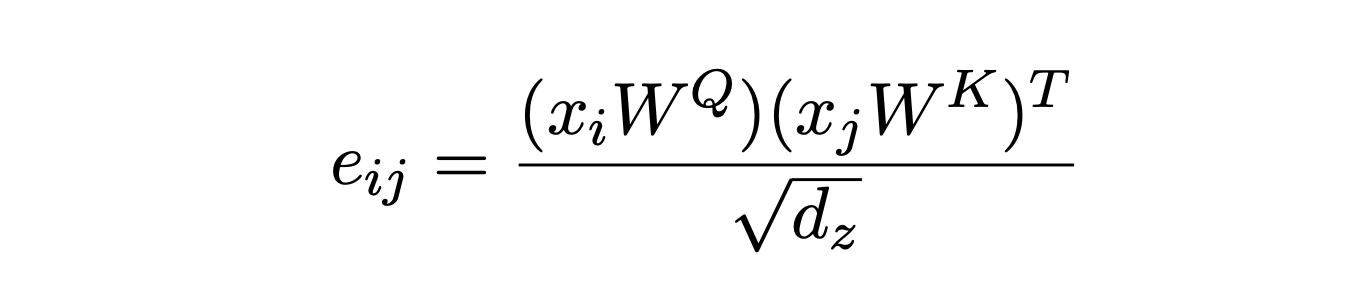

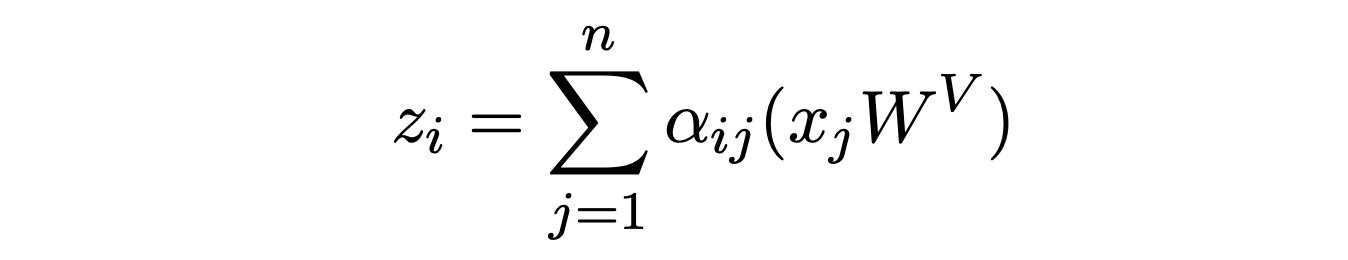
在 Paper 中,引入了 \(w^{k}=(w_{-k}^{K} … w_{k}^{K})\) 和 \(w^{v}=(w_{-k}^{V} … w_{k}^{V})\),其中 K 表示相对位置的范围,即:某个 token 左侧和右侧最大关注的 Token 数量,\(w^{k}、w^{v}\) 就是分别对应了两个相对位置矩阵中的向量,这两个也是学习的参数。那么,这两个用于表示相对位置的向量如何应用到 self attention 计算中呢?
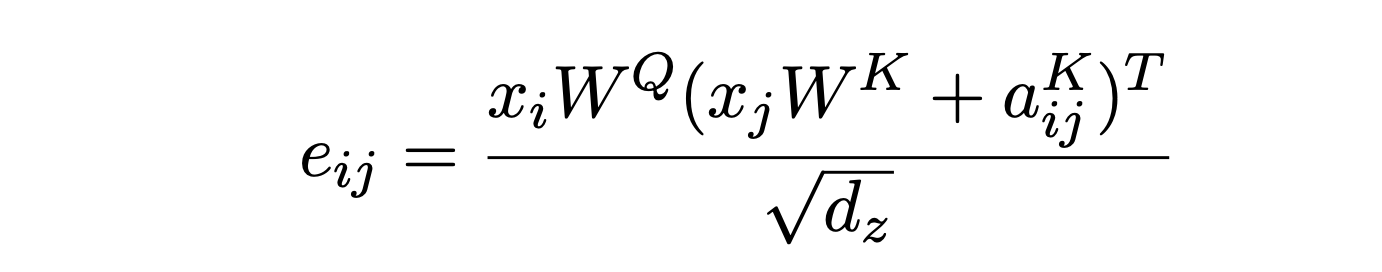
我们可以看到在计算 \(e_{ij}\) 时,将 i 和 j 之间的相对位置编码 K 引入,即:i -j 位置的相对位置编码向量。我们知道该公式表示 i 的 query 向量对 j 的 key 向量的注意,此时加入 \(a_{ij^{K}\) 就表示在计算中引入了可学习的相对位置编码。
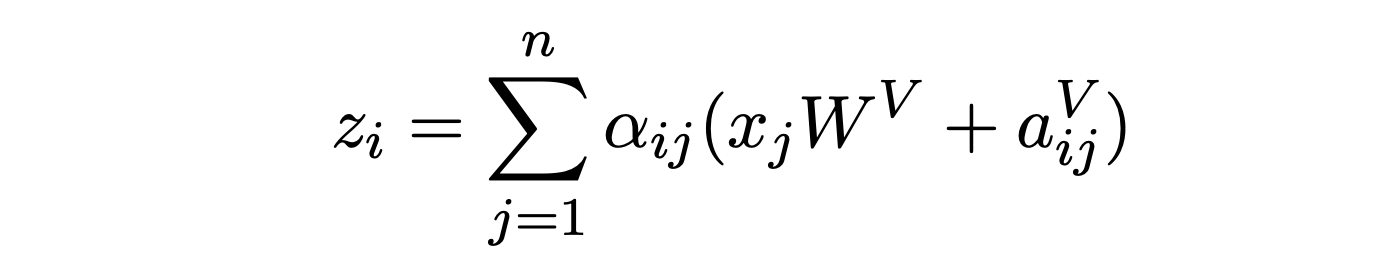
在计算自注意力向量表示时,将引入了 latex]a_{ij^{V}[/latex],这表示最终生成的注意力向量也引入一种相对位置信息,当然这个相对位置信息也是可学习的。
从这里可以看到,谷歌的这篇论文中认为,对 KEY、VALUE 使用了不同的相对位置编码参数。
4. 《Transformer-XL: Attentive Language Models Beyond a Fixed-Length Context》
Paper:https://arxiv.org/pdf/1803.02155.pdf
从这里看到,这两种计算相对位置的编码方式还是有所区别的:
- 谷歌的这篇论文中,计算注意力分数时,引入了相对位置信息,并且在计算最终的注意力向量表示时也引入了相对位置信息
- Transformer-XL 中则只在计算注意力分数时,引入了相对位置信息。并且,更细粒度的对内容和位置分别使用了不同的相对位置编码参数。

 冀公网安备13050302001966号
冀公网安备13050302001966号