scikit-learn 中 GaussianMixture 类是对高斯混合模型算法的实现，它包含了一些用于控制混合高斯模型（GMM）的初始化、训练方式和模型的其他设置。

1. 参数

1.1 基本参数

1. n_components：指定高斯混合模型中的高斯分布数量，也就是成分数。每个成分对应一个高斯分布，用来拟合数据的不同簇。
2. tol：这个设定的阈值就是判断收敛的标准。比如，设定值为 0.001，表示当增益（对数似然）小于这个阈值时，认为收敛已完成。
3. reg_covar：在协方差矩阵中添加的正则化项，防止计算过程中的数值不稳定，尤其是在协方差接近奇异矩阵时。
4. max_iter：最大迭代次数。如果模型在达到该次数之前没有收敛，则终止训练。
5. n_init：用于多次初始化以防止局部最优，每次初始化都会产生一个模型，然后选择最优的一个。
6. weights_init：可以为模型的各成分指定初始权重。默认值为 None，将由算法估计。
7. means_init：用于指定初始均值。默认值为 None，，由算法估计。
8. precisions_init：指定初始协方差矩阵的逆（精度矩阵）。默认是 None，由模型自己估计。
9. random_state：控制随机数生成器的种子，使得结果可复现。
10. warm_start：如果设置为 True，模型会在后续调用 fit 时使用上次训练的结果作为初始值。
11. verbose：控制输出的详细程度。值越大输出越多，常用于调试。
12. verbose_interval：指定输出信息的频率。每 verbose_interval 次迭代输出一次信息，用于监控训练过程。

1.2 covariance_type

协方差矩阵中的对角线元素代表了各个特征的方差，即它们各自的变化范围；而对角线以外的元素代表特征之间的协方差。所以，协方差矩阵不仅描述了每个特征自身的分布，还包含了特征之间的相互关系。

• 正值：表示两个特征往往会一起增加或减少。例如，如果一个特征值增大时，另一个特征值也倾向于增大，那么它们的协方差就是正的。
• 负值：表示一个特征增加而另一个减少，反之亦然。说明它们通常朝相反的方向变化。
• 零值：表示两个特征之间没有关联，即它们的变化没有明显的相关关系。

sckit-learn 的 GaussianMixture 在实现时，考虑了四种协方差矩阵的类型：

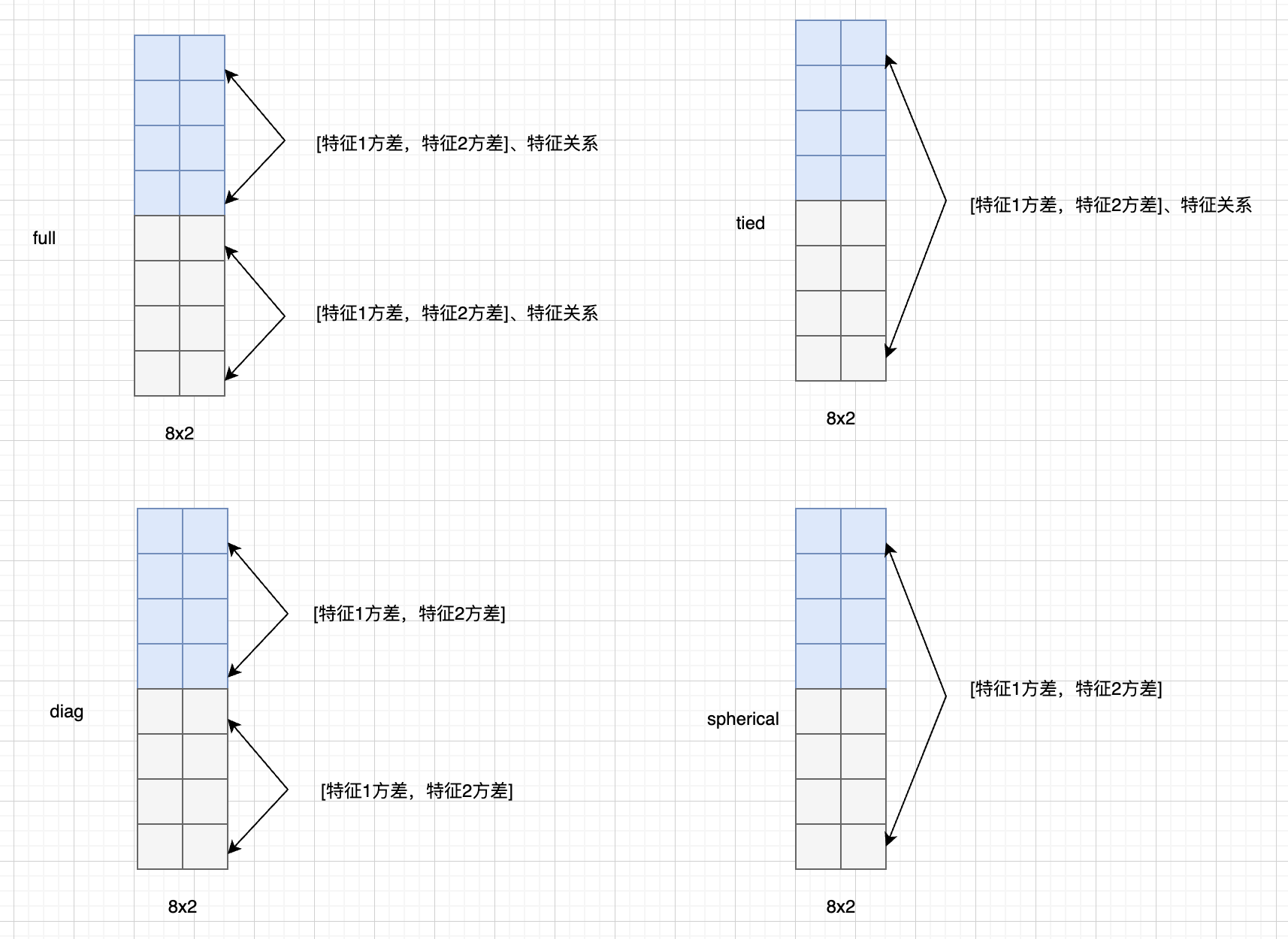
• full 适合描述复杂的数据分布；
• tied 适合类别间分布相似的数据；
• diag 适合特征独立或弱相关的数据；
• spherical 适合特征方差相同、无方向性的简单数据。

1.3 init_params

GaussianMixture 的 init_params 参数用于控制 GMM 的初始参数值。不同的初始值设定方式会对模型的收敛速度和最终结果有影响。

• kmeans：采用 KMeans 聚类算法将数据分配到最适合的高斯分量中，使模型从较合理的初始值出发，因此在多数情况下收敛速度较快，结果也较稳定；

• k-means++：使用 k-means++ 方法来选择初始均值，它在选择初始中心时尽量使这些中心彼此之间距离较远，从而提高模型的收敛质量；

• random：随机初始化。适合用于快速测试，但收敛速度可能较慢，且容易陷入局部最优解；

• random_from_data：随机选择数据点作为初始均值。该方法避免了完全随机分布的均值初始化，但其效果仍不如 kmeans 和 k-means++ 稳定。

2. 方法

from sklearn.mixture import GaussianMixture
from sklearn.datasets import make_blobs
import numpy as np


x, y = make_blobs(n_samples=10, n_features=2, random_state=42)
estimator = GaussianMixture(n_components=2, random_state=42)
estimator.fit(x)


# 1. 属性和方法
def test01():

    # 1.1 函数
    inputs = np.random.rand(2, 2)
    y_pred = estimator.predict(inputs)  # 预测标签
    print('预测标签：', y_pred)

    y_prob = estimator.predict_proba(inputs)  # 预测概率
    print('预测概率：', y_prob.tolist())

    samples = estimator.sample(3)  # 生成样本
    print('生成样本：', samples)

    # 1.2 属性
    print('成分均值：', estimator.means_)
    print('协方差矩阵：', estimator.covariances_)
    # 协方差矩阵的逆
    print('精度矩阵：', estimator.precisions_)
    print('成分权重：', estimator.weights_)


# 2. 评估方法
def test02():

    # 1. 样本平均对数似然值
    print('lhd:', estimator.score(x))
    # 每个样本的对数似然值
    print('lhd:', estimator.score_samples(x).sum() / x.shape[0])

    # 2. 赤池信息准则（Akaike Information Criterion, AIC）
    print('aic:', estimator.aic(x))

    # 3. 贝叶斯信息准则（Bayesian Information Criterion, BIC）
    print('bic:', estimator.bic(x))


if __name__ == '__main__':
    test02()

程序中提到的 AIC 和 BIC 计算公式如下：

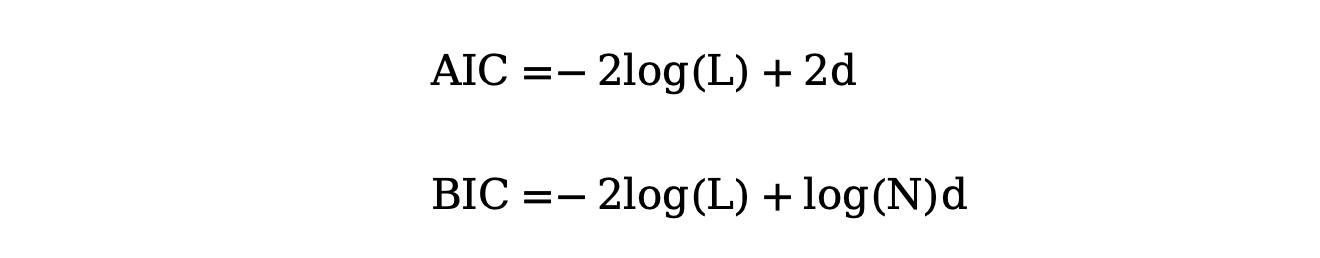
其中：

• log(L) 表示所有样本的最大对数似然值和
• d 表示参数量
• N 表示样本数量

• AIC：由日本统计学家赤池弘次提出，它衡量了模型对数据的拟合度与模型复杂度之间的平衡。AIC 值越小，说明模型在拟合度和复杂度之间达到了较好的平衡，相对更优。
• BIC：是基于贝叶斯统计理论，它同样考虑了模型对数据的拟合度和模型复杂度，但是对模型复杂度的程度比 AIC 更加严厉。当样本量较大时，BIC 更倾向于选择简单的模型，避免过拟合。