GMM 假设数据是由多个高斯分布混合而成,接下来,我们将会探讨 GMM 是如何根据训练数据得到这些不同的高斯分布参数:
- 均值向量:每个高斯分布的均值。
- 协方差矩阵:描述每个高斯分布的形状和方向。
- 混合系数:表示每个高斯分布在总体分布中的权重,总和为 1。
估计高斯混合模型的参数,我们并不知道数据属于哪个分布,这是典型的包含隐藏变量的参数估计问题。对于这个问题可以使用期望最大化(EM)算法进行参数估计。EM 算法核心步骤:
- 首先,基于某种策略给所有的参数进行初始化(不准确)
- 然后,重复执行 E 步和 M 步的计算,直到算法收敛,得到估计的参数
- E 步:在给定当前参数下,计算每个数据点属于每个高斯分布的后验概率
- M 步:根据 E 步骤计算的后验概率,重新估计模型参数
重复 E 步骤和 M 步骤,直到模型参数的变化小于设定的阈值,或者达到最大迭代次数。
接下来,我们通过一个简单的计算案例来演示 GMM 的拟合过程。假设数据如下,我们使用包含两个高斯分布的 GMM 模型来对该数据进行拟合:
| 数据 | 高斯分布 |
| 2.1 | ? |
| 2.9 | ? |
| 3.2 | ? |
| 5.5 | ? |
| 4.8 | ? |
| 9.1 | ? |
| 10.3 | ? |
| 10.8 | ? |
1. 初始模型参数
初始化参数如下表所示:
| 均值 μ | 方差 \( σ^2 \) | 混合系数 π | |
| 分布1 | 1.0 | 2.0 | 0.5 |
| 分布2 | 2.0 | 5.0 | 0.5 |
2. E 步计算
E 步骤:计算后验概率。对于每个数据点,计算其属于两个高斯分布的后验概率。
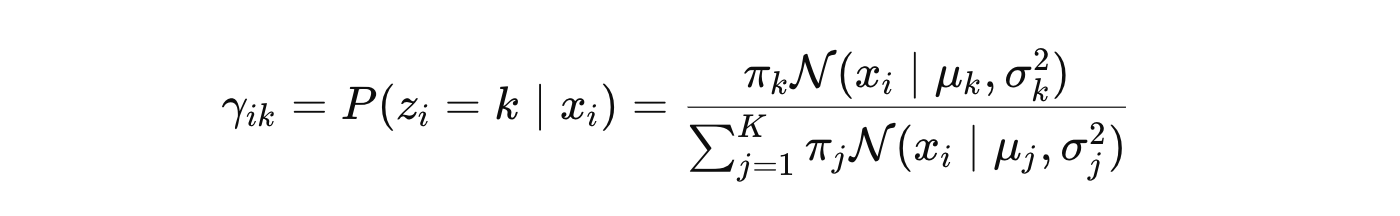
其中:

高斯分布的概率密度函数为:
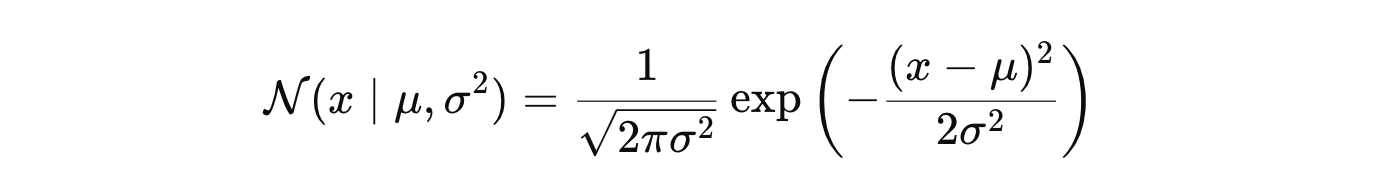
| 数据 | 高斯分布1 | 高斯分布2 |
| 2.1 | 0.53908 | 0.46092 |
| 2.9 | 0.41015 | 0.58985 |
| 3.2 | 0.35255 | 0.64745 |
| 5.5 | 0.03295 | 0.96705 |
| 4.8 | 0.08566 | 0.91434 |
| 9.1 | 0.00002 | 0.99998 |
| 10.3 | 0.00000 | 1.00000 |
| 10.8 | 0.00000 | 1.00000 |
3. M 步计算
M 步骤:更新参数使用 E 步骤中的后验概率值,更新模型参数:



| 均值 μ | 方差 \( σ^2 \) | 混合系数 π | |
| 分布1 | 2.84581 | 0.63733 | 0.17755 |
| 分布2 | 6.78731 | 10.08798 | 0.82245 |
重复 E 和 M 步骤数次。在每次迭代中,均值和协方差逐步调整,最终使得两个高斯分布能够更好地拟合数据。
4. 得到估计参数
当 EM 算法迭代过程中,一般满足以下任意条件,就会停止迭代,此时获得模型的估计参数:
- 参数变化小于设定阈值:一种常用的收敛条件是当模型参数(均值、方差、混合系数)之间的变化小于某个设定的阈值时停止迭代
- 对数似然增量小于设定阈值:在每次迭代中,EM 算法会计算当前模型参数下的数据对数似然。可以设定一个阈值 ϵ,当两次迭代的对数似然增量小于 ϵ 时,认为算法已收敛
- 最大迭代次数:有时,尽管参数或对数似然值的变化仍未满足阈值,但经过大量迭代后收敛速度可能减慢,因此可以设定最大迭代次数。这可以避免算法陷入无效的长时间迭代。
例如:当迭代 5 次之后,得到的参数如下:
| 均值 μ | 方差 \( σ^2 \) | 混合系数 π | |
| 分布1 | 2.73203 | 0.21254 | 0.31929 |
| 分布2 | 7.66143 | 7.82931 | 0.68071 |




 冀公网安备13050302001966号
冀公网安备13050302001966号