回归决策树（Decision Tree Regression）是一种使用决策树进行回归分析的方法。与分类决策树不同，回归决策树用于预测连续型的目标变量，而不是离散的类别。

1. 构建决策树

我们使用 MSE（平均平方误差）来演示决策树构建过程。测验、性别为特征，期末为目标值。

序号	测验	性别	期末
0	80	男	84.2
1	82	女	80.6
2	85	男	80.1
3	90	女	90
4	86	男	83.2
5	82	女	87.6
6	78	男	79.4

由于我们的数据集中包含类别特征，scikit-learn 的回归决策树 API 是无法直接处理，所以需要将其转换为独热编码（说白了，就是转换为数值表示）：

序号	测验	性别_女	性别_男	期末
0	80	0	1	84.2
1	82	1	0	80.6
2	85	0	1	80.1
3	90	1	0	90
4	86	0	1	83.2
5	82	1	0	87.6
6	78	0	1	79.4

我们将每个特征值升序排列：

测验	性别_女	性别_男
78	0	0
80	1	1
82
85
86
90

计算相邻两个数的均值作为切分点：

测验	性别_女	性别_男
79	0.5	0.5
81
83.5
85.5
88

	测验=79	测验=81	测验=83.5	测验=85.5	测验=88	性别_女=0.5	性别_男=0.5
	0.0	5.760	10.327	9.562	8.061	4.087	15.902
<=	6 79.4	0 84.2 6 79.4	0 84.2 1 80.6 5 87.6 6 79.4	0 84.2 1 80.6 2 80.1 5 87.6 6 79.4	0 84.2 1 80.6 2 80.1 4 83.2 5 87.6 6 79.4	0 84.2 2 80.1 4 83.2 6 79.4	1 80.6 3 90.0 5 87.6
	12.655	15.184	17.096	11.560	0.000	15.902	4.087
>	0 84.2 1 80.6 2 80.1 3 90.0 4 83.2 5 87.6	1 80.6 2 80.1 3 90.0 4 83.2 5 87.6	2 80.1 3 90.0 4 83.2	3 90.0 4 83.2	3 90.0	1 80.6 3 90.0 5 87.6	0 84.2 2 80.1 4 83.2 6 79.4
MSE	12.655	20.944	27.423	21.122	8.061	19.989	19.989

当我们选择特征 测验 的 88 切分点，能够获得最小的预测误差。我们进行此次分裂：

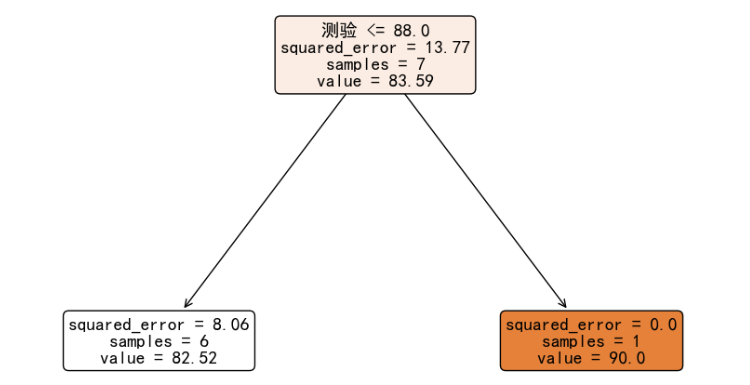
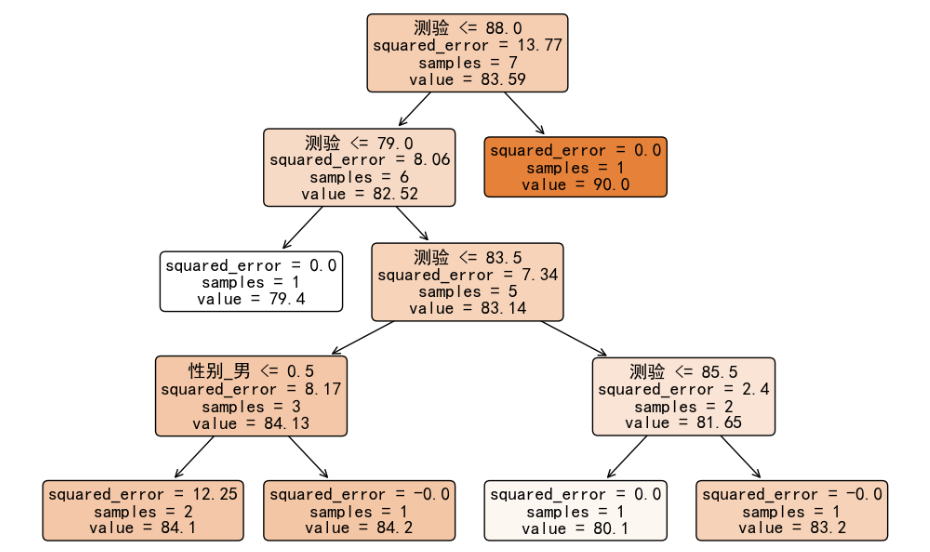
右子树的误差为 0，而左子树的误差有 8.06，我们可以继续对左子树的 6 个样本使用平方误差进行分裂，以获得在训练集上更高的精度。进行完全生长之后的决策树如下图所示：

2. 分裂准则

在使用 from sklearn.tree import DecisionTreeRegressor 构建回归决策树时，其分裂增益方式 criterion 就有以下四个选择：

2.1 squared_error

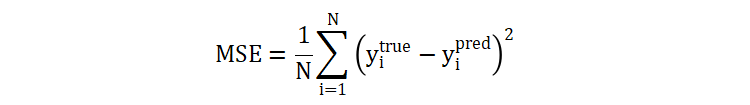
squared_error 是我们使用 scikit-learn 构建回归决策树时使用的默认分裂增益计算方法。当我们选择一个切分点时，会将树分为左右子树，我们使用 MSE 分别计算两个子树的 MSE，并加起来得到一个分裂后的误差，选择误差最小的切分点作为最终选择的切分点。

2.2 absolute_error

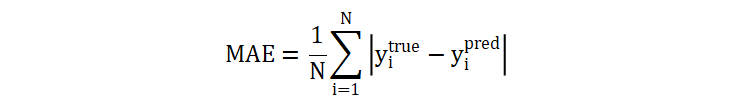
absolute_error 计算的是预测和真实之间的绝对误差，这种方式相对于 squared_error，对噪声相对不敏感。对噪声敏感意味着，数据集中的噪声数据带来的误差可能会影响到切分点的选择，进而影响到整个决策树的构建。由于 squared_error 通过平方会缩放误差，而 absolute_error 则计算真实误差，相对于前者相对更加不容易受到异常值的影响。

2.3 poisson

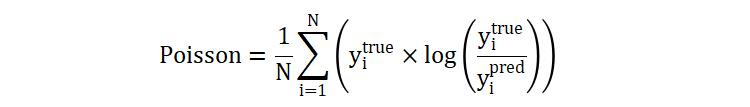
泊松偏差的原本的计算公式如下：

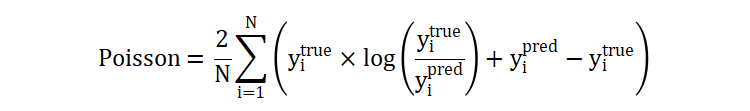
针对决策树场景，有：

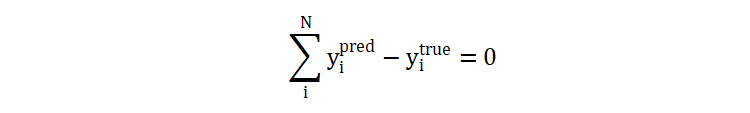
原公式中的 2 舍弃，就得到现在的计算公式。公式中，最终的部分是对数计算部分，这部分的值是可正可负：

1. 当预测值小于真实值时，得到的 Poisson 偏差就大于 0，表示模型给出的预测值偏小；
2. 当预测值大于真实值时，得到的 Poisson 偏差就小于 0，表示模型给出的预测值偏大；
3. 当预测值等于真实值时，表示预测的结果精确，没有偏差。

所以，从这个过程来看，poisson 更加倾向于选择偏差较小的切分点。

2.4 friedman_mse

• mean_left 表示左子树样本平均值
• mean_right 表示右子树样本平均值
• diff 表示左右子树输出差值
• n_left 表示分裂之后，左子树样本数量
• n_right 表示分裂之后，右子树样本数量

1. 如果 \(n\_left × n\_right\) 较大，说明分裂之后左右子树样本数量较为均衡，反之，则说明左右子树样本数量不平衡；
2. 如果 \(diff^{2}\) 较大，说明左右子树的输出差异较大，有助于区分不同的数据点。反之，则说明两个子树输出的差异较小。

至此，回归决策树的内容就讲解完毕了，希望对你有所帮助。