聚类（Clustering）指的是将一组数据点按照某种规则或者方法分成多个组或簇，使得同一组内的数据点在某种意义上更相似，而不同组之间的数据点相对较不相似。

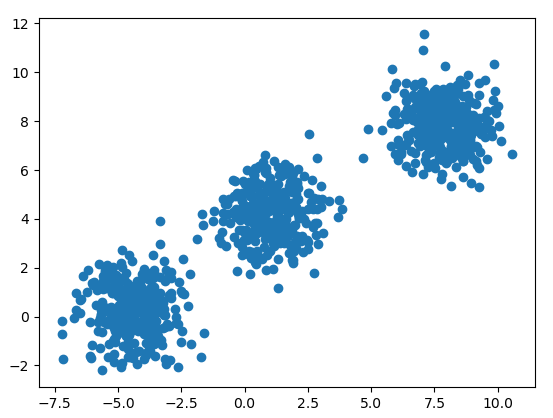
聚类时，可以基于数据分布、基于数据密度、基于数据相似度、基于图结构等等方法。K 均值聚类是基于数据相似度（欧式距离）将数据集聚类为多个簇，每个簇都会有一个质心，表示簇的中心位置（每个维度上的平均值）。

1. 算法原理

使用 K 均值聚类的步骤如下：

随机选择 K 个初始质心
计算每个数据点到每个质心的距离，并将每个数据点分配给最近的质心
对每个簇重新计算质心，即簇内所有数据点的平均值
重复步骤2和步骤3，直到质心不再变化或达到预设的迭代次数

简言之：K 均值聚类的目标，是找到 K 个质心，使得每个数据点到所属质心的距离最小。

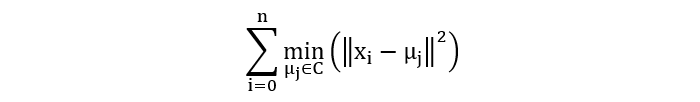
1.1 随机质心

1.2 距离计算

1.3 更新质心

重复 1.2~1.3 步骤，直到质心不再发生变化，或者达到指定的迭代次数。最终得到的聚类结果：

2. 聚类优化

K 均值聚类的结果、效率会受到多种因素的影响，例如：初始质心的位置会影响聚类的效果，而数据量则会影响聚类的效率。

KMeans 的实现中主要提供了两方面的优化：

优化训练速度，使用 elkan 算法
优化初识质心，使用 kmean++ 算法

2.1 elkan

K-means 算法的工作原理是首先选择 K 个质心，然后将每个数据点分配给距离它最近的质心。之后，算法会更新质心的位置，并重复此过程，直到算法收敛，即质心的位置不再发生变化。

在 K-means 算法的每个迭代步骤中，都需要计算每个数据点到所有质心的距离。这可能会导致大量的计算，特别是当数据集较大时。

Elkan 算法是一种用于加速 K-means 算法的启发式方法。它利用三角形不等式来提前终止某些距离的计算，从而降低算法的计算时间。

Elkan K-means 为了能够判断提前终止哪些样本点需要额外维护一些数据结构，这会增加算法的内存开销。对于非常大的数据集，这种额外的内存开销可能会成为一个问题。

2.2 kmeans++

质心的初始位置会影响到聚类的效果。质心初始化太近：

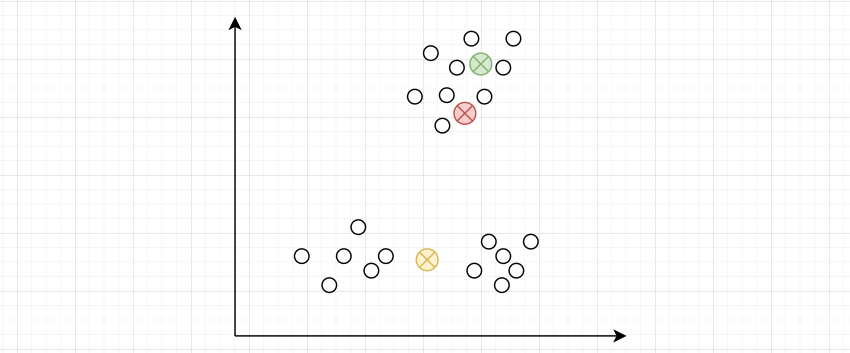
质心初始化过于分散，相互距离太远，在聚类中可能会受到异常点的影响。

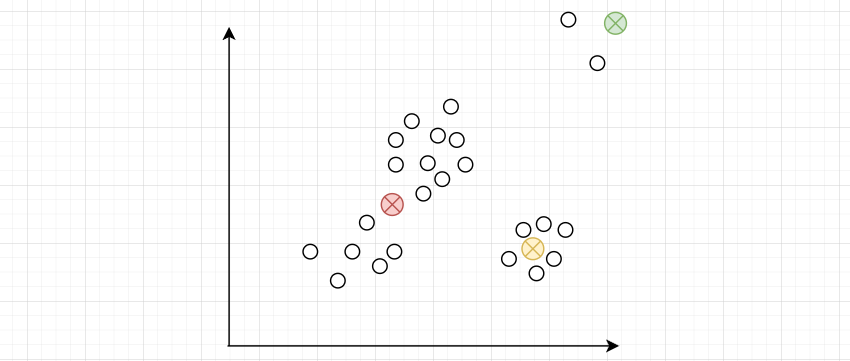
所以，质心在初始化的时候，要分散一些，尽可能地代表其所在类别的中心位置。这样的条件仍然是很灵活的，不容易达成，所以实际在实现的时候，要经过多次随机（有控制的随机），每次初始化分散一些。

k-means++ 是对 K 均值聚类算法初始质心的优化算法。假设数据如下，并且我们要初始化 3 个质心：

(1, 1)

(2, 1)

(4, 3)

(5, 4)

(8, 7)

(9, 8)

算法步骤：

随机选择一个数据点作为第一个质心：\(C_{1}=(1, 1)\)
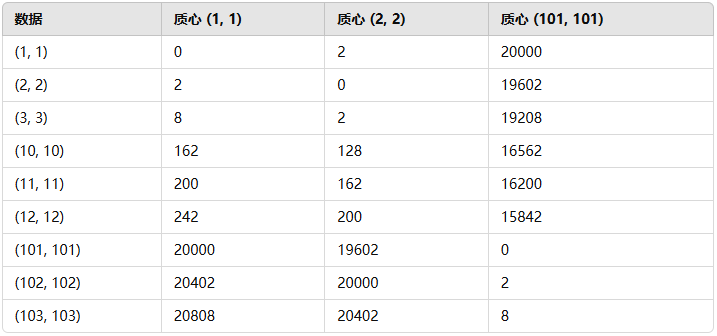
计算所有数据点到距离最近质心的距离平方 \(D(x)^2\)

数据点	质心	距离	概率
(2, 1)	(1, 1)	1	0.00421941
(4, 3)	(1, 1)	13	0.05485232
(5, 4)	(1, 1)	25	0.10548523
(8, 7)	(1, 1)	85	0.35864979
(9, 8)	(1, 1)	113	0.47679325

根据概率分布，(9, 8) 有最高的概率被选为下一个质心。此时，假设我们就选择 (9, 8) 作为第二个质心。
计算所有数据点到距离最近质心的距离平方 \(D(x)^2\)

数据点	质心	距离	概率
(2, 1)	(1, 1)	1	0.02439024
(4, 3)	(1, 1)	13	0.31707317
(5, 4)	(1, 1)	25	0.6097561
(8, 7)	(9, 8)	2	0.04878049

根据概率分布，(5, 4) 有最高的概率被选择为下一个质心。此时，假如我们随机选择了 (4, 3) 作为第三个质心。
此时，3 个质心选择结束。

3. K 值选择

K 值的选择对算法的性能影响很大：

K 值太小： 会使得不同类别的数据点被误归类到同一簇中，即不同簇的样本之间差异较大，导致聚类结果质量差。

K 值太大：过大的 K 值会导致可能将原本属于同一簇的样本分配到不同的簇中。这样虽然每个簇的样本间距离更小，但整体的泛化能力较差。并且，过多的簇可能导致一些簇内的样本数量过少，甚至出现空簇的情况，聚类结果不稳定。也会导致计算量的增加，因为算法需要对更多的簇进行初始化和迭代，计算成本随之升高。

那么，如何确定 K 值？

我们可以通过 “肘” 部法来确定 K 值。步骤如下：

尝试不同的 K 值，通常从较小的值开始增加，例如：1、3、5、7
对于每个 K 得到其 inertia_ 值，即所有样本点到它们最近的簇中心的距离的平方和
以 K 值作为横轴，每个 K 对应的 inertia_ 值作为纵轴，绘制出一个折线图（肘部图）
在肘部图中，通常会出现一个类似肘部的拐点（elbow point）。这个拐点对应的 K 值就是相对最优的簇数。

肘部法的基本思想是，随着 K 值的增加，inertia_ 的下降幅度会逐渐变小。而最佳的 K 值通常出现在这个下降幅度显著变缓的位置，形象地称为肘部。

from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt
import numpy as np
import warnings
warnings.filterwarnings('ignore')


def generate_dataset():
    # 初始化聚类数据
    # n_samples：生成样本数量
    # centers：质心数量
    # cluster_std：每个类别的标准差
    # center_box：质心坐标的生成范围
    # random_state：随机数种子
    x, y = make_blobs(centers=3,
                      n_samples=10000,
                      center_box=(-10, 10),
                      cluster_std=2,
                      random_state=42)

    return x, y


def test01():
    # 生成数据
    x, y = generate_dataset()
    plt.scatter(x[:, 0], x[:, 1], c=y)
    plt.show()

    # n_init：初始化多少次质心
    # n_clusters：聚类质心数量
    # init：质心初始化方法 random 或者 k-means++
    # algorithm：聚类优化方法，lloyd 或者 elkan
    estimator = KMeans(n_clusters=3,
                       n_init=10,
                       init='k-means++',
                       algorithm='lloyd',
                       random_state=42)
    y_pred = estimator.fit_predict(x)
    print(y_pred)




def test02():
    # 生成数据
    x, y = generate_dataset()
    # 候选 K 值
    cluster_list = [1, 3, 5, 7, 9]
    inertia_list = []

    # 计算不同 K 下的误差平方和
    for n in cluster_list:
        estimator = KMeans(n_clusters=n)
        estimator.fit_predict(x)
        inertia_list.append(estimator.inertia_)

    # 绘制肘部图
    plt.plot(cluster_list, inertia_list)
    plt.grid()
    plt.show()


if __name__ == '__main__':
    test02()

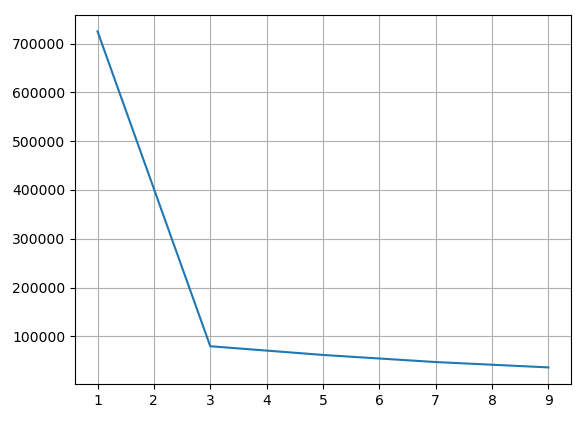
我们可以看到，当 n_clusters = 3 时，误差平方和下降趋于平缓，可以作为合理的 K 值。

K 均值聚类（K-means）