Complement Naive Bayes (CNB) 是对多项式朴素贝叶斯 (Multinomial Naive Bayes, MNB) 的一种改进。它主要针对多项式朴素贝叶斯在处理类别不平衡问题时表现不佳的情况进行优化。

https://people.csail.mit.edu/jrennie/papers/icml03-nb.pdf

1. 问题场景

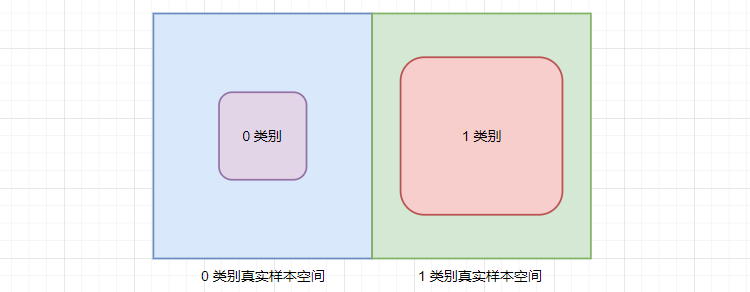
在多项式朴素贝叶斯中，当训练样本在类别之间不平衡时，朴素贝叶斯会对较少样本的类别产生偏差，从而选择不佳的决策边界权重。

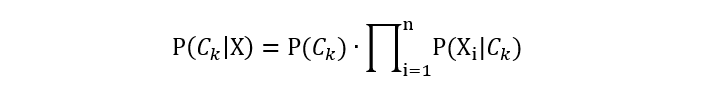
例如：对于二分类问题，其中 0 类样本占比 10%，1 类样本占比 90%。其影响如下：

先验概率：巨大差异会导致模型对多数类更有偏向。例如：即使某个样本的特征符合 0 类，模型也可能会因为较大的先验概率而将其误分类为 1 类。
条件概率：当类别不平衡时，样本数量较少的类别的特征频率估计可能不准确，尤其是当样本数量极少时。

简言之，训练样本的类别不平衡会导致多项式朴素贝叶斯的先验概率、条件概率估计不准确，使得：

分类偏差：模型可能更倾向于预测为样本数量较多的类别，导致分类结果的偏差。
召回率低：对于样本数量少的类别，模型的召回率可能会较低。

2. 算法思想

补集朴素贝叶斯算法针对多项式朴素贝叶斯在类别不平衡时的问题进行了一些优化（根据 scikit-learn 实现）。

去掉先验概率：在补集朴素贝叶斯中，计算时去掉了先验概率的影响。传统的多项式朴素贝叶斯会考虑每个类别的先验概率。然而，在类别不平衡的情况下，大类别的先验概率会过高，从而导致模型偏向于大类别。补集朴素贝叶斯通过去掉先验概率，使得模型在预测时更加关注特征的条件概率，从而减轻类别不平衡的影响。

使用补集条件概率：补集朴素贝叶斯使用补集条件概率来替代基于类别样本的条件概率。在传统的多项式朴素贝叶斯中，条件概率是基于某个类别的数据集频率来计算的。而在补集朴素贝叶斯中，条件概率是基于该类别的补集中的特征频率来计算的。这样可以有效地降低大类别对条件概率计算的影响，使得模型对小类别更加敏感，从而提高分类性能。

什么是补集？

对于每个类别 \(C_{k}\)，补集 \(C_{k}’\) 指的是除去 \(C_{k}\) 该类别之外的所有类别的样本集合。

假设包含 0、1、2 三个类别的样本集
0 类别的补集就是 1、2 类别所有样本
1 类别的补集就是 0、2 类别所有样本
2 类别的补集就是 0、1 类别所有样本

对于特征 \(X_{i}\)，补集朴素贝叶斯计算的是特征在补集 \(C_{k}’\) 中出现的概率 \(P(X_{i}|C_{k}’)\)。

0 类别每个特征的条件概率基于 1、2 样本集进行计算
1 类别每个特征的条件概率基于 0、2 样本集进行计算
2 类别每个特征的条件概率基于 0、1 样本集进行计算

注意：根据补集计算得到的特征的条件概率，并不是 \(C_{k}\) 类别特征的真实条件概率。我们这里计算在补集下的条件概率，目的是为了通过补集反估计出 \(C_{k}\) 特征的条件概率。

因为补集代表原类别的对立部分，若特征在补集中的条件概率越小，意味着在原类别中的条件概率越大。

举个例子：

我们想估计 A 公司的营收情况，但由于对 A 公司的营收数据掌握较少，无法得到有效的估计。然而，我们掌握了 A 公司的竞争公司 B 的大量营收数据，可以利用这些数据来反推 A 公司的营收状况。

例如：

如果 B 公司的营收很高，那么可以推测 A 公司的市场份额可能被挤压，导致 A 公司的营收较低。
反之，如果 B 公司的营收较低，那么 A 公司可能在市场竞争中处于有利地位，因而其营收可能较高。

这个过程类似于 CNB 的基于补集的思想，即利用已知的其他类别（补集）的数据来反推目标类别（原类别）的概率分布。通过这种方式，我们可以在数据不平衡或缺乏数据的情况下，仍然对目标类别做出合理的预测。

当使用基于补集的条件概率计算新样本所属的类别时，会将该样本归类为补集条件概率乘积最小的类别。

由于这是个最小化问题，而多项式朴素贝叶斯中是最大化问题，为了能够统一，所以对补集条件概率取反，转换为最大化问题。

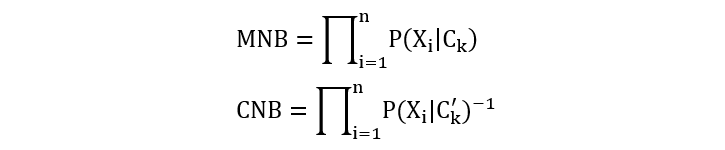
为什么使用补集能够优化类别不平衡的场景？

在传统的多项式朴素贝叶斯中，对于少数类别 \(C_{k}\)，样本数量较少，导致估计条件概率 \(P(X|C_{k})\) 时可能存在较大的不准确性。补集朴素贝叶斯通过计算补集 \(C_{k}’\) 的条件概率来反推 \(C_{k}\) 的条件概率。

从理论上讲，补集代表了原类别的对立部分。如果一个特征在补集中出现的概率很低，那么在原类别中出现的概率相对来说会较高。因此，通过计算补集的条件概率并取反，我们可以更好地推断出原类别的条件概率。

3. 计算过程

3.1 训练过程

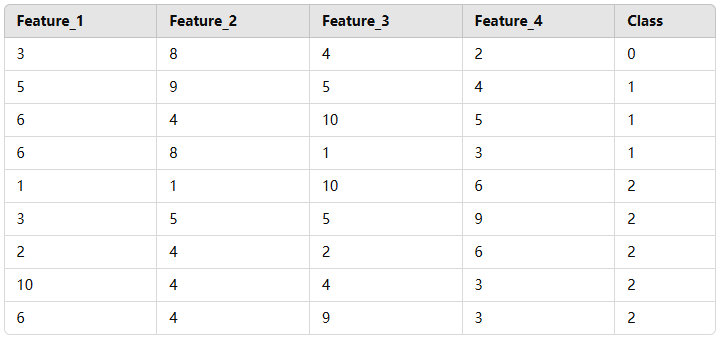
我们接下来使用下面的数据来讲解 CNB 算法的训练和推理过程（该案例仅仅为了演示计算过程）。

特征1	特征2	特征3	特征4	标签
1	2	3	4	0
2	3	4	5	0
5	6	7	8	0
6	7	8	9	0
21	23	25	27	1

第 1 步：计算每个特征的总的统计量

特征1	特征2	特征3	特征4
35	41	47	53

第 2 步：计算各个类别特征的统计量

类别	特征1	特征2	特征3	特征4
0	14	18	22	26
1	21	23	25	27

第 3 步：由于第二步得到的各个类别的统计量，由于采样的原因，有可能为 0，这就意味着该特征并不发挥作用。通过增加平滑计算，赋予它们一个小的非零概率，使其也能够发挥影响。默认平滑系数 α 为 1。

特征1	特征2	特征3	特征4
35 + 1	41 + 1	47 + 1	53 + 1

第 4 步：计算各个类别补集，以及补集条件概率。

类别	特征1	特征2	特征3	特征4
0	22	24	26	28
1	15	19	23	27

类别	特征1	特征2	特征3	特征4
0	22/100	24/100	26/100	28/100
1	15/84	19/84	23/84	27/84

第 5 步：计算概率的对数值

类别	特征1	特征2	特征3	特征4
0	log(22/100)	log(24/100)	log(26/100)	log(28/100)
1	log(15/84)	log(19/84)	log(23/84)	log(27/84)

第 6 步：对对数概率取反（可以理解为得到由补集反估计得到的类别的对数条件概率）

类别	特征1	特征2	特征3	特征4
0	-log(22/100)=1.51413	-log(24/100)=1.42712	-log(26/100)=1.34707	-log(28/100)=1.27297
1	-log(15/84)=1.72277	-log(19/84)=1.48638	-log(23/84)=1.29532	-log(27/84)=1.13498

至此，训练过程结束。

3.2 预测过程

特征1	特征2	特征3	特征4	标签
6	7	8	9	？

计算属于 0 类别的分数：

6 * 1.51413 + 7 * 1.42712 + 8 * 1.34707 + 9 * 1.27297 = 41.3079

计算属于 1 类别的分数：

6 * 1.72277 + 7 * 1.48638 + 8 * 1.29532 + 9 * 1.13498 = 41.3186

由于属于 1 类别分数较大，最终预测为 1 类别。

这里需要注意，这个案例仅仅是为了解释 CNB 算法训练和推理过程，直观上看，待预测样本应该属于 0 类别，实际预测为 1 类别。

4. 源码阅读

from sklearn.naive_bayes import ComplementNB
from sklearn.naive_bayes import CategoricalNB
import numpy as np


if __name__ == '__main__':

    # 训练数据
    inputs = np.array([[1, 2, 3, 4],
                       [2, 3, 4, 5],
                       [5, 6, 7, 8],
                       [6, 7, 8, 9],
                       [21, 23, 25, 27]], dtype=np.float32)
    labels = np.array([0, 0, 0, 0, 1])

    # 算法训练
    estimator = ComplementNB()
    estimator.fit(inputs, labels)

    # 特征重要性
    print('特征\n', estimator.feature_log_prob_)

    # 对数似然
    inputs = [[6, 7, 8, 9]]
    scores = estimator.predict_joint_log_proba(inputs)
    print('分数:', scores)

    # 标签预测
    y_pred = estimator.predict(inputs)
    print('标签:', y_pred)

程序执行结果：

特征
 [[1.51412773 1.42711636 1.34707365 1.27296568]
 [1.7227666  1.48637782 1.29532258 1.13497993]]

分数: [[41.30786115 41.31864438]]

标签: [1]

补集朴素贝叶斯（Complement NB）