多项式朴素贝叶斯（Multinomial Naive Bayes）是朴素贝叶斯分类器的一种变体，主要用于文本分类任务。它是一种基于概率的分类算法，通常适用于处理离散型特征，特别是在文本分类问题中表现良好。

《垃圾邮件识别器》（四）算法理论

我们以下面数据为例，介绍下多项式朴素贝叶斯的计算过程。

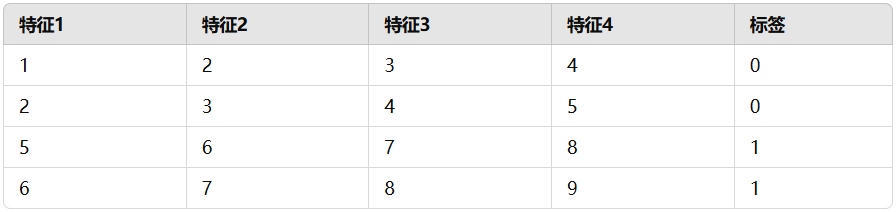
1. 训练过程

训练过程是计算每个特征在类别条件的对数概率、以及类别对数先验概率。

1.1 类别 0 对数条件概率

特征总和：3 + 5 + 7 + 9 = 24

进行拉普拉斯平滑：

特征总和：3 + 5 + 7 + 9 = 24 + 4（特征数量） = 28

计算对数条件概率：

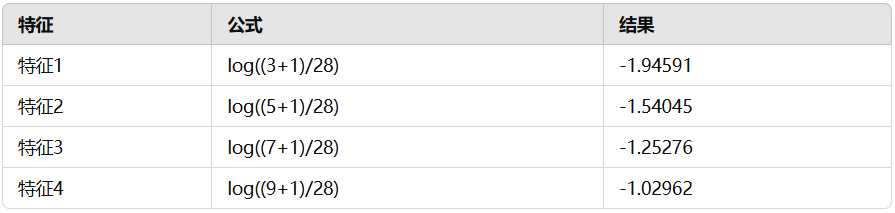
1.2 类别 1 对数条件概率

特征总和：11 + 13 + 15 + 17 = 56
进行拉普拉斯平滑：

特征总和：1 + 13 + 15 + 17 = 56 + 4（特征数量） = 60

计算对数条件概率：

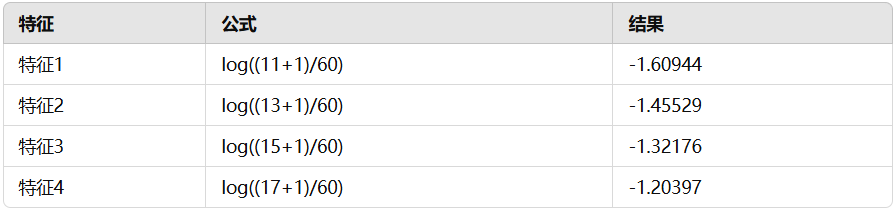
2. 预测过程

2.1 计算 0 类别分数

计算每个特征的对数条件概率

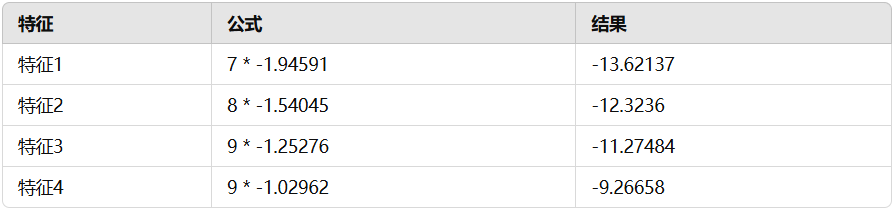
计算对数条件概率 + 先验概率之和：

7 * -1.94591 + 8 * -1.54045 + 9 * -1.25276 + 9 * -1.02962 -0.69315（先验） = -47.1795

2.2 计算 1 类别分数

计算每个特征的对数条件概率

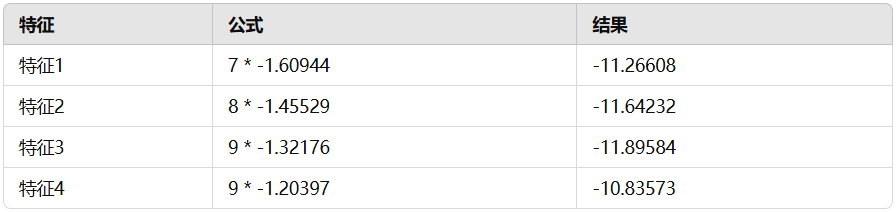
计算对数条件概率 + 先验概率之和：

7 * -1.60944 + 8 * -1.45529 + 9 * -1.32176 + 9 * -1.20397 -0.69315（先验） = -46.333

由于 \( -46.333 > -47.1795 \)，所以该样本归类为 1 类别。