长短期记忆网络（Long Short-Term Memory，LSTM）是一种特殊的循环神经网络（RNN），与传统的 RNN 相比，在处理涉及较长距离时间依赖的任务中表现出更强的能力。

1. 算法原理

LSTM 为了解决传统 RNN 面临的长期依赖问题，引入了细胞状态（Cell State）、门控单元（Gate）实现长期信息的记忆。

• 细胞状态：用来携带长期信息的主要通道
• 门控单元：用于控制信息的流动
  • 输入门：控制当前输入信息有多少信息被写入细胞状态
  • 遗忘门：控制前一时刻的细胞状态有多少信息被保留到当前时刻
  • 输出门：控制当前细胞状态的多少信息输出作为隐藏状态传递到下一时刻

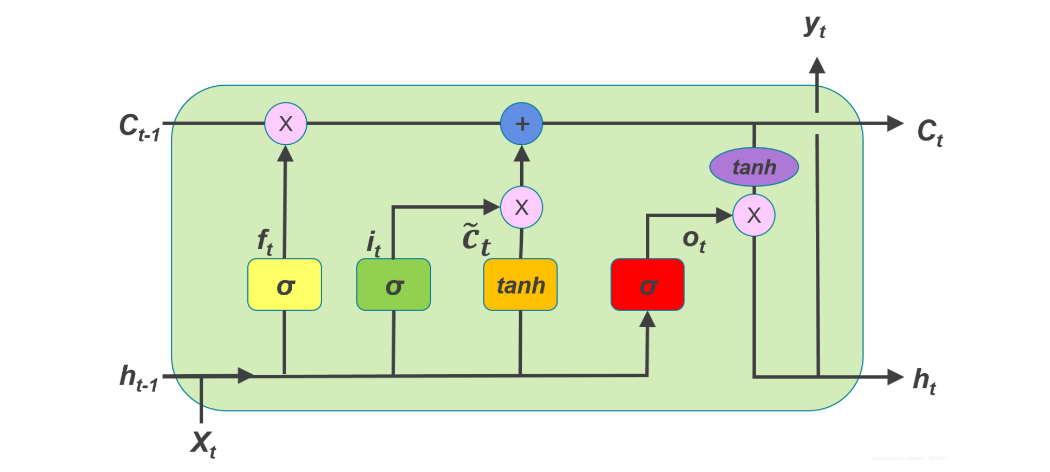
• \(h_{t-1}\)表示上一个时间步的隐藏状态
• \(h_{t}\) 表示当前时间步的隐藏状态
• \(X_{t}\) 表示当前时间步的输入
• \(C_{t-1}\) 表示上一个时间步记忆的长期依赖信息
• \(C_{t}\) 表示当前时间步记忆的长期依赖信息
• \(\sigma\) 表示 sigmoid 激活函数
• \(tanh\) 表示 tanh 激活函数
• \(g_{t}\) 表示当前输入的信息（正：积极信息，负：负面信息）
• \(f_{t}\) 表示遗忘门，保留多少细胞信息
• \(i_{t}\) 表示输入门，保留多少输入信息到细胞状态
• \(o_{t}\) 表示输出门，输出多少细胞信息

我们针对上图的理解：

• 细胞状态会累积序列中所有的元素的信息
• 通过门控机制来控制历史信息、输入的信息、输出信息保留多少

相关的计算公式如下：

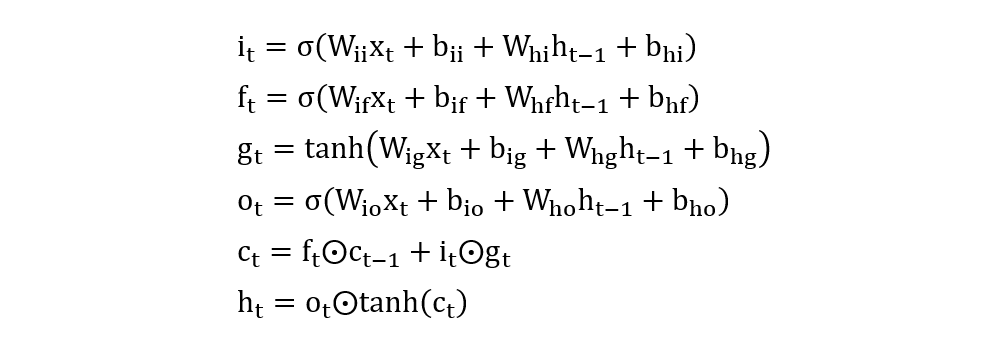
2. 算法使用

import torch
import torch.nn as nn


def test01():

    torch.manual_seed(42)
    lstm = nn.LSTM(input_size=2, hidden_size=4, num_layers=1, bidirectional=False)
    # 1. 重要：输入形状(seq_len, batch_size, dim)
    inputs = torch.randn(3, 1, 2)

    # 初始化细胞状态、隐藏状态(可省略)
    # 形状：(num_layers * num_directions, batch_size, hidden_size)
    h_0 = torch.zeros(1, 1, 4)
    c_0 = torch.zeros(1, 1, 4)

    # 2. 重要：输入参数和输出结果
    # output: 每个元素对应的隐藏状态
    # hn：最后一个元素的隐藏状态
    # cn：最后一个元素的细胞状态
    output, (hn, cn) = lstm(inputs, (h_0, c_0))
    print('output shape:', output.shape)
    print('hn shape:', hn.shape)
    print('cn shape:', cn.shape)
    print(output)
    print(hn)
    print(cn)


def test02():
    torch.manual_seed(42)

    lstm = nn.LSTMCell(input_size=2, hidden_size=4)
    inputs = torch.randn(3, 1, 2)

    # 初始化细胞状态、隐藏状态
    hx = torch.zeros(1, 4)
    cx = torch.zeros(1, 4)

    # 计算每一个时间步
    for idx in range(inputs.shape[0]):
        hx, cx = lstm(inputs[idx], (hx, cx))

    print(hx)
    print(cx)


if __name__ == '__main__':
    test01()
    print('-' * 70)
    test02()

程序输出结果：

output shape: torch.Size([3, 1, 4])
hn shape: torch.Size([1, 1, 4])
cn shape: torch.Size([1, 1, 4])
tensor([[[-0.0382, -0.0373, -0.0662, -0.0236]],

        [[-0.1445, -0.0549, -0.0175, -0.0920]],

        [[-0.0706, -0.0701, -0.0888, -0.1205]]],
       grad_fn=<MkldnnRnnLayerBackward0>)
tensor([[[-0.0706, -0.0701, -0.0888, -0.1205]]], grad_fn=<StackBackward0>)
tensor([[[-0.1892, -0.1798, -0.1382, -0.2783]]], grad_fn=<StackBackward0>)
----------------------------------------------------------------------
tensor([[-0.0706, -0.0701, -0.0888, -0.1205]], grad_fn=<MulBackward0>)
tensor([[-0.1892, -0.1798, -0.1382, -0.2783]], grad_fn=<AddBackward0>)