AUC（Area Under the Curve）是一种常用二分类评估方法，它指的是 ROC 曲线（Receiver Operating Characteristic Curve）下的面积。

1. ROC

ROC（Receiver Operating Characteristic）曲线是一个图形工具，用于展示分类器在不同阈值下的表现。该曲线的纵轴为真正例率（True Positive Rate，TPR），横轴为假正例率（False Positive Rate，FPR）。

• TPR：在所有的正样本中预测为正样本的比例
• FPR：在所有的负样本中预测为正样本的比例

我们以下面的数据集为例，来了解如何基于模型的预测结果（基于预测概率，非预测标签）来绘制 ROC 曲线。

真实标签	预测概率
1	0.9
0	0.7
1	0.8
0	0.6
0	0.5
0	0.4

根据预测概率降序排列：

真实标签	预测概率
1	0.9
1	0.8
0	0.7
0	0.6
0	0.5
0	0.4

绘制 ROC 曲线：

1. 阈值：0.9
   1. 原本为正例的 1、3 号的样本中 3 号样本被分类错误，则 TPR = 1/2 = 0.5
   2. 原本为负例的 2、4、5、6 号样本没有一个被分为正例，则 FPR = 0
2. 阈值：0.8
   1. 原本为正例的 1、3 号样本被分类正确，则 TPR = 2/2 = 1
   2. 原本为负例的 2、4、5、6 号样本没有一个被分为正例，则 FPR = 0
3. 阈值：0.7
   1. 原本为正例的 1、3 号样本被分类正确，则 TPR = 2/2 = 1
   2. 原本为负类的 2、4、5、6 号样本中 2 号样本被分类错误，则 FPR = 1/4 = 0.25
4. 阈值：0.6
   1. 原本为正例的 1、3 号样本被分类正确，则 TPR = 2/2 = 1
   2. 原本为负类的 2、4、5、6 号样本中 2、4 号样本被分类错误，则 FPR = 2/4 = 0.5
5. 阈值：0.5
   1. 原本为正例的 1、3 号样本被分类正确，则 TPR = 2/2 = 1
   2. 原本为负类的 2、4、5、6 号样本中 2、4、5 号样本被分类错误，则 FPR = 3/4 = 0.75
6. 阈值 0.4
   1. 原本为正例的 1、3 号样本被分类正确，则 TPR = 2/2 = 1
   2. 原本为负类的 2、4、5、6 号样本全部被分类错误，则 FPR = 4/4 = 1

由不同阈值下的 (FPR, TPR) 构成的 ROC 图像为：

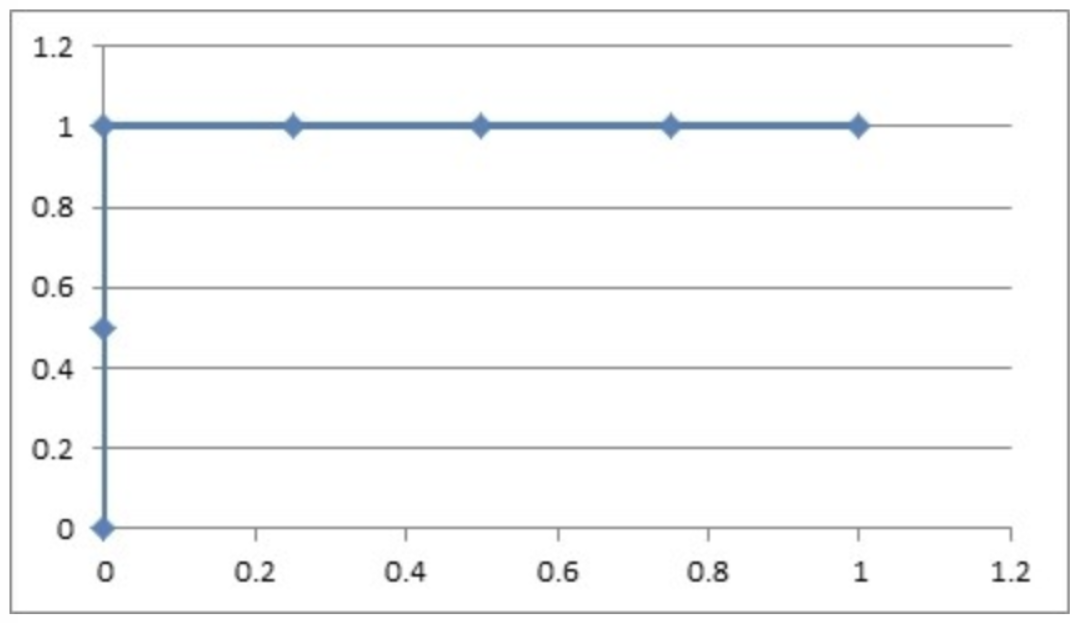
如果模型得到上图的 ROC 曲线，我们一般认为该模型为完美的分类器模型。但是，我们大多数得到的 ROC 曲线类似下面：

• 图中任取一点表示在某个阈值下，正样本的预测准确率，负样本的预测错误率
• (0, 0) 表示所有的正样本都预测错误，所有的负样本都预测正确
• (1, 0) 表示所有的正样本都预测错误，所有的负样本都预测错误
• (1, 1) 表示所有的正样本都预测正确，所有的负样本都预测错误
• (0, 1) 表示所有的正样本都预测正确，所有的负样本都预测正确

2. AUC

我们在观察 ROC 曲线时，一般认为：

1. 曲线越靠近 (0, 1) 点则模型对正负样本的辨别能力就越强
2. 曲线越靠近 (0, 1) 点则 ROC 曲线下面的面积就会越大

所以，我们就想使用 ROC 曲线下面的面积 AUC 来量化分类器的性能：

1. AUC 范围在 [0, 1] 之间
2. 当 AUC = 1.0 时，该模型被认为是完美的分类器
3. 当 AUC = 0.5 时，模型区分正负样本的就会变得模棱两可，即：随意拿出一对正负样本，模型只有 50% 的概率能够将识别。

import numpy as np
from sklearn.metrics import roc_curve, auc, roc_auc_score


def test():

    y_true = [1, 0, 1, 0, 0, 0]
    y_prob = [0.9, 0.7, 0.8, 0.6, 0.5, 0.4]

    # 计算 (fpr, tpr)
    fpr, tpr, thresholds = roc_curve(y_true, y_prob, pos_label=1)
    print('阈值:', thresholds)
    print('FPR:', fpr)
    print('TPR:', tpr)

    # 计算 AUC 值
    auc_score = auc(fpr, tpr)
    print('AUC:', auc_score)

    # 计算 AUC 值
    auc_score = roc_auc_score(y_true, y_prob)
    print('AUC:', auc_score)


if __name__ == '__main__':
    test()

阈值: [inf 0.9 0.8 0.4]
FPR: [0. 0. 0. 1.]
TPR: [0.  0.5 1.  1. ]
AUC: 1.0
AUC: 1.0

• 只要所有正样本的预测概率大于负样本，则 AUC 值就是 1，AUC 关注的是模型对正负样本的排序能力
• 即使模型没有很好地区分正类和负类，AUC仍然可能很高。
• AUC不能提供有关模型性能的详细信息，比如模型在不同阈值下的表现如何。因此，它缺乏透明性，不能告诉你模型在特定阈值下的表现情况。
• AUC的计算受数据分布的影响，特别是在样本较少或者有噪音的情况下，AUC的可靠性可能会降低。
• AUC只关注样本的排序，而不考虑具体的概率值。这意味着如果模型的输出只是大致排序正确，但具体的概率值并不准确，AUC仍然可能很高。

3. 多分类

import numpy as np
from sklearn.metrics import roc_curve, auc, roc_auc_score

y_label = [2, 0, 2, 2, 0, 0, 2, 1, 2, 2]
y_proba = [[0.70, 0.20, 0.10],
           [0.05, 0.50, 0.45],
           [0.33, 0.34, 0.33],
           [0.25, 0.25, 0.50],
           [0.60, 0.30, 0.10],
           [0.10, 0.10, 0.80],
           [0.40, 0.40, 0.20],
           [0.15, 0.75, 0.10],
           [0.20, 0.50, 0.30],
           [0.55, 0.25, 0.20]]

# 1. ovr
# n_class 个二分类器：[0 rest]、[1 rest]、[2 rest]
# 计算第一个分类器中 0 类别 AUC 值
# 计算第二个分类器中 1 类别 AUC 值
# 计算第三个分类器中 2 类别 AUC 值
# 将得到的 3 个 AUC 值取平均，得到 ovr 多分类场景下的 AUC 值
def test01():

    auc_score = roc_auc_score(y_label, y_proba, multi_class='ovr')
    print('OVR AUC:', auc_score)

    # 手动计算
    aucs = []
    for label in [0, 1, 2]:
        y_temp_label = np.where(np.array(y_label) == label, 1, 0)
        y_temp_proba = np.array(y_proba)[:, label]
        auc = roc_auc_score(y_temp_label, y_temp_proba)
        aucs.append(auc)
    print('OVR AUC:', np.mean(aucs))


# 2. ovo
# N(N-1)/2 个二分类器：[0 1]、[0 2]、[1 2]
# 分别计算第一个分类器中 0、1 类别的 AUC 值
# 分别计算第二个分类器中 0、2 类别的 AUC 值
# 分别计算第三个分类器中 1、2 类别的 AUC 值
# 将得到的 6 个 auc 值取均值即得到 ovo 多分类场景下的 auc 值
def test02():

    auc_score = roc_auc_score(y_label, y_proba, multi_class='ovo')
    print('OVO AUC:', auc_score)

    # 手动计算
    from itertools import combinations
    y_temp_label = np.array(y_label)
    y_temp_proba = np.array(y_proba)
    aucs = []

    for a, b in combinations([0, 1, 2], 2):

        # 筛选出 a b 两类别的标签
        label = y_temp_label[(y_temp_label == a) | (y_temp_label == b)]

        # 以 a 类别作为正样本计算 auc 值
        a_label = np.where(label == a, 1, 0)
        a_proba = y_temp_proba[:, a][(y_temp_label == a) | (y_temp_label == b)]
        a_auc = roc_auc_score(a_label, a_proba)

        # 以 b 类别作为正样本计算 auc 值
        b_label = np.where(label == b, 1, 0)
        b_proba = y_temp_proba[:, b][(y_temp_label == a) | (y_temp_label == b)]
        b_auc = roc_auc_score(b_label, b_proba)

        aucs.append(a_auc)
        aucs.append(b_auc)

    print('OVO AUC:', np.mean(aucs))


if __name__ == '__main__':
    test01()
    test02()

OVR AUC: 0.5952380952380952
OVR AUC: 0.5952380952380952
OVO AUC: 0.6481481481481483
OVO AUC: 0.6481481481481483