基尼指数是决策树算法中用于评估特征分裂质量的一个关键指标，分裂后子节点的基尼指数越低，表示子节点的纯净度越高。

1. 基尼不纯度

基尼不纯度（Gini impurity）是衡量变量不纯度的一个指标。基尼不纯度越高，表示数据的不纯度或混乱程度越大。计算公式：

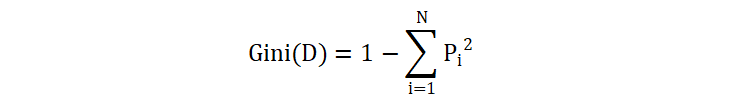
其中，\(P_i\)​ 是数据集 \(D\) 中属于第 \(i\) 类的样本占总样本数的比例，\(N\) 是类别的数量。

变量 X	变量 Y
α	A
α	A
β	B
α	A
β	B
α	B

我们使用上面的公式来计算变量 X 和 Y 的不纯度：

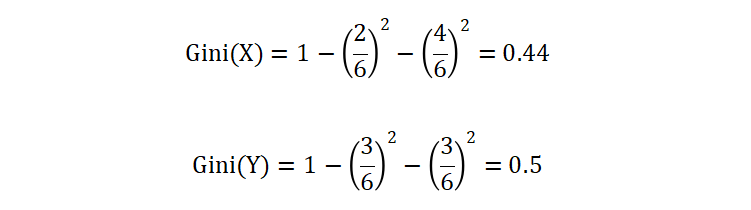
从计算结果来看，变量 Y 的基尼不纯度要高于 X。

2. 基尼指数

在决策树的构建过程中，我们需要选择一个特征和一个切分点来分割数据集。为了找到最佳的划分，我们可以使用基尼指数。基尼指数是用于衡量选择某特征进行划分后所得到的加权基尼不纯度。其计算公式如下：

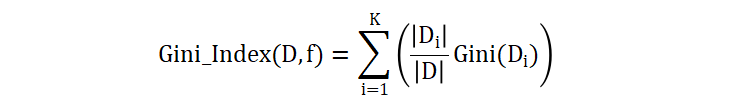
其中，\(D\)​ 是当前数据集，\(f\)​ 是待评估的特征，\(K\)​ 是特征 \(f\) 可能取值的数量，\(|D_i|\)​​ 是特征 \(f\) 取值为 i 时的子数据集。

变量 X	变量 Y
α	A
γ	A
β	B
β	A
α	B
α	B

我们现在选择变量 X 进行数据集划分，并计算变量 Y 的加权基尼不纯度。首先，我们先计算每个子集的基尼不纯度：

• 当 X = α 时，变量 Y = ABB
• 当 X = β 时，变量 Y = BA
• 当 X = γ 时，变量 Y = A

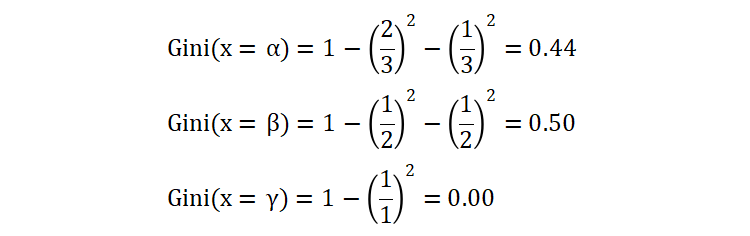
然后根据每个子集的占比，加权求和，得到基尼指数，如下：

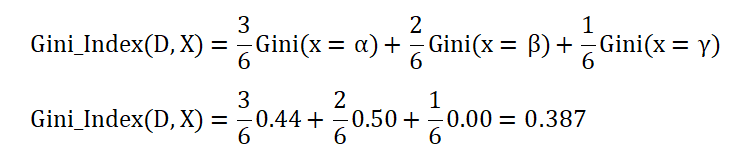
3. 构建决策树

我们通过一个例子，来了解如何基于基尼指数来构建决策树。

序号	婚姻	收入(万)	拖欠贷款
0	单身	6	否
1	已婚	8	否
2	单身	9	否
3	已婚	6	否
4	离异	7	是
5	已婚	9	否
6	离异	8	否
7	单身	6	是
8	已婚	6	否
9	单身	9	是

接下来，基于上面的数据集，使用基尼指数来构建决策树。这里需要注意的是，我们使用的 scikit-learn 中的决策树 API 是无法直接处理类别特征数据，需要先将所有的类别特征进行独热编码（就是转换为数字），方便后续处理。

序号	婚姻_单身	婚姻_已婚	婚姻_离异	收入(万)	拖欠贷款
0	1	0	0	6	否
1	0	1	0	8	否
2	1	0	0	9	否
3	0	1	0	6	否
4	0	0	1	7	是
5	0	1	0	9	否
6	0	0	1	8	否
7	1	0	0	6	是
8	0	1	0	6	否
9	1	0	0	9	是

我们将所有的特征的值升序排列：

婚姻_单身	婚姻_已婚	婚姻_离异	收入(万)
0	0	0	6
1	1	1	7
			8
			9

取相邻两个数的均值作为切分点，如果有 N 个元素，则将会获得 N-1 个切分点：

婚姻_单身	婚姻_已婚	婚姻_离异	收入(万)
0.5	0.5	0.5	6.5
			7.5
			8.5

接下来，计算每个切分点的基尼指数（每个切分点通过取 <= 和 >，将数据集划分为两部分）：

	婚姻_单身=0.5	婚姻_已婚=0.5	婚姻_离异=0.5	收入(万)=6.5	收入(万)=7.5	收入(万)=8.5
	0.278	0.500	0.375	0.375	0.480	0.408
<=	1 否 3 否 4 是 5 否 6 否 8 否	0 否 2 否 4 是 6 否 7 是 9 是	0 否 1 否 2 否 3 否 5 否 7 是 8 否 9 是	0 否 3 否 7 是 8 否	0 否 3 否 4 是 7 是 8 否	0 否 1 否 3 否 4 是 6 否 7 是 8 否
	0.500	0.000	0.500	0.444	0.320	0.444
>	0 否 2 否 7 是 9 是	1 否 3 否 5 否 8 否	4 是 6 否	1 否 2 否 4 是 5 否 6 否 9 是	1 否 2 否 5 否 6 否 9 是	2 否 5 否 9 是
Gini	0.367	0.300	0.400	0.416	0.400	0.419

从计算结果来看，当使用特征 婚姻_已婚，并且选择 0.5 作为切分点时，基尼指数最低，即：能够最大程度提高原始数据集的纯度，我们进决策树分裂：

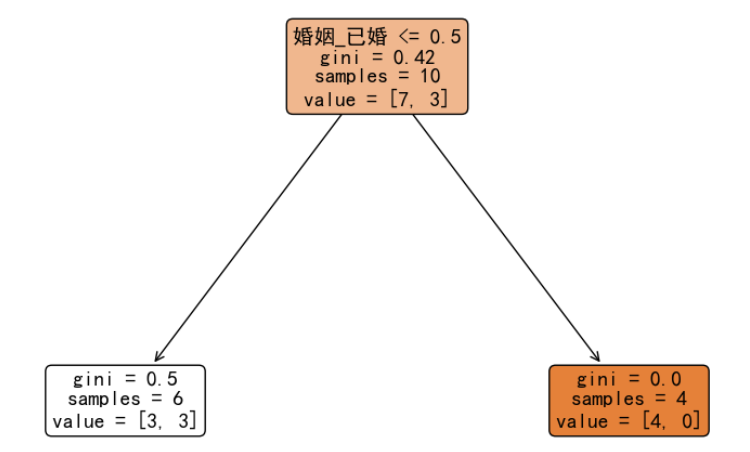
我们发现右子树已经达到最大纯度，不需要继续分裂。而左子树由于没有达到最大纯度，所以要继续按照前面的方法，计算这 6 条数据在每个特征分裂点的基尼指数，从而选择最小切分点继续分裂。完整分类之后的决策树如下图所示：

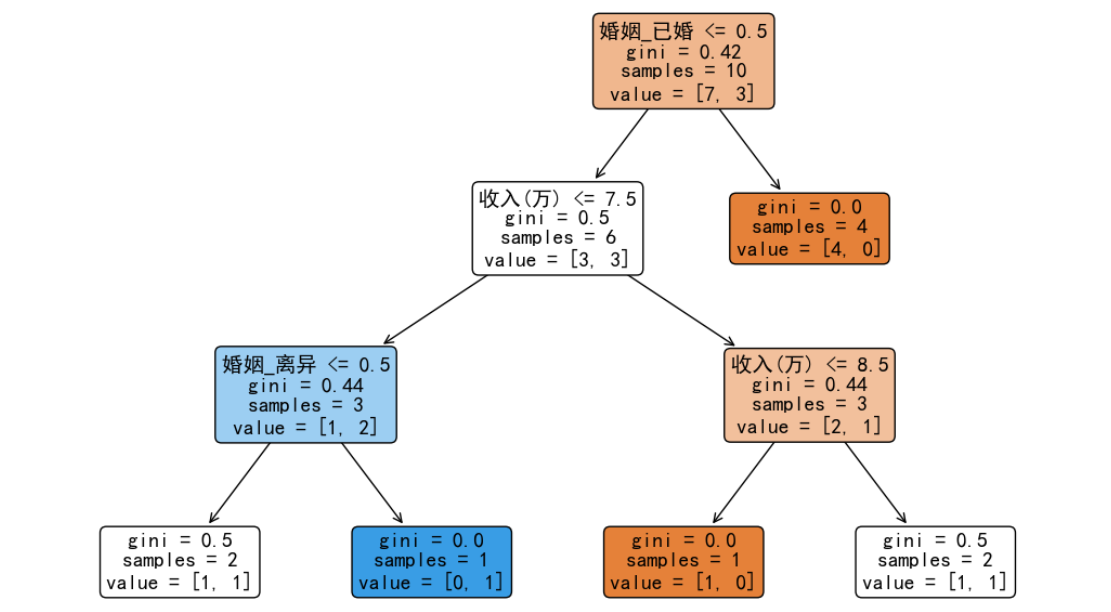
至此，关于基尼指数构建决策树的内容就讲解完毕，希望对你有所帮助。