在 scikit-learn 的决策树实现中，使用 CCP（Cost-Complexity Pruning）代价复杂度剪枝，用于避免过拟合并提高决策树的泛化能力。

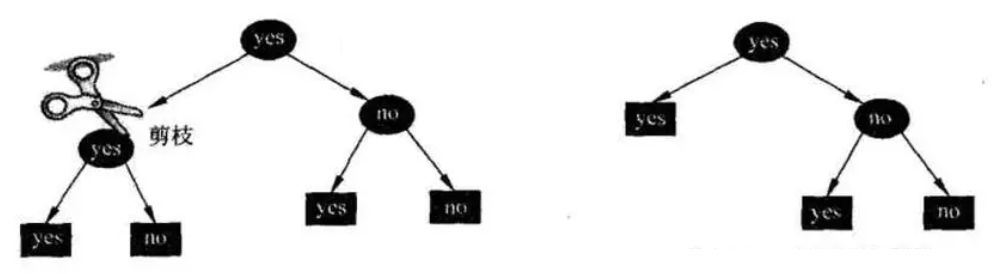
1. 剪枝原理

决策树中包含了很多子树，一棵子树是否应该剪掉，得通过某个指标来对其代价复杂度进行度量，CCP 使用下面的指标来进行度量：

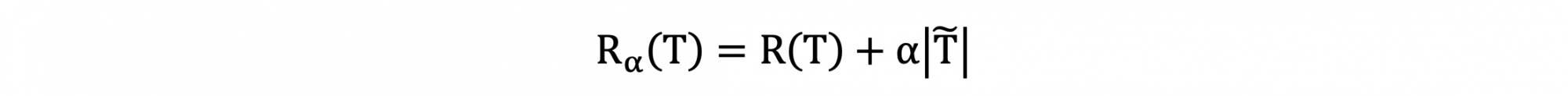
R(T) 表示子树的加权不纯度（以基于基尼不纯度的分类决策树为例）
\(\tilde{T}\) 表示子树的叶子节点数量
α 表示调节参数

通过 CCP 公式，我们可以从不纯度和叶子结点数量两个角度来度量一棵树的复杂度。其中，不纯度表示树的拟合效果，叶子结点数量表示树的复杂度。

如果 \(R_{\alpha}(T)\) 值比较大，说明决策树更加复杂
如果 \(R_{\alpha}(T)\) 值比较小，说明决策树更加简单

在公式中，超参数 α 用来调节度量决策树代价复杂度时，我们更倾向于关心不纯度，还是叶子结点数量：

如果设置较大的 α 值，说明我们更加关心叶子结点数量
如果设置较小的 α 值，说明我们更加关心叶树的不纯度

另外，我们还需要理解一点是：树的剪枝过程并不是只剪一次，如果一直剪下去的话，最后只会剩下一个根节点。并且，每次剪枝都会在上次剪枝后的树上进行。关于 α 还应该理解：

如果 α 值过大，倾向于过度对决策树进行剪枝
如果 α 值较小，倾向于对决策树进行更加保守的剪枝

2. 复杂度计算

树的复杂度计算包括对某个子树的计算、以及对叶子结点的计算。树的复杂度计算公式如下：

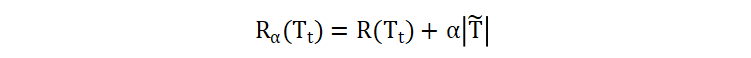
\(T_t\) 表示以结点 t 为根节点的子树
\(\tilde{T}\) 表示以结点 t 为根节点的子树的叶子结点数量

如果要计算某个叶子结点的复杂度 \(R(t)\)，则使用下面的公式：

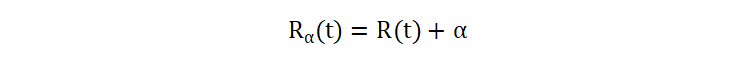
R(t) 表示某个叶子结点的加权不纯度。

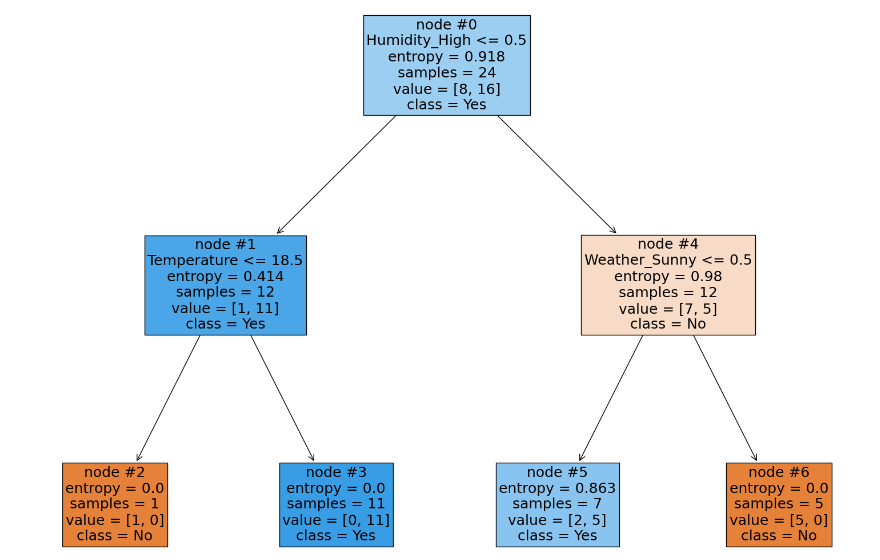
我们以下面的树（使用熵来度量每个节点的不纯度，值越大，不纯度越高）为例，来手动计算下树和叶子结点的复杂度：

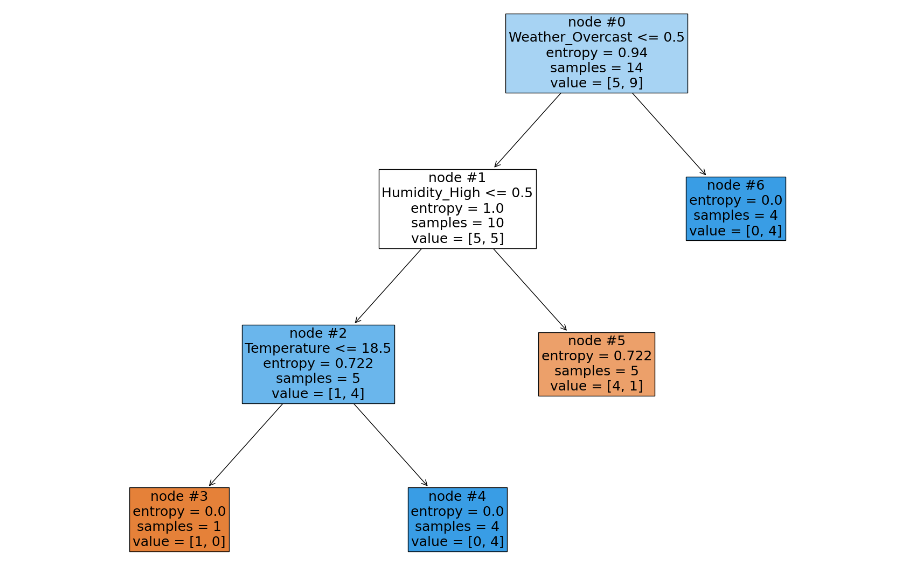
计算 R(t=0) 树的 CCP 复杂度，并且 α =0.1，则：

加权不纯度：

第 3 号叶子结点：0.0 * 1/14 = 0
第 4 号叶子结点：0.0 * 4/14 = 0
第 5 号叶子结点：0.722 * 5/14 = 0.258
第 6 号叶子结点：0.0 * 4/14

叶子结点复杂度：0.1 * 4 = 0.4

最终得到 R(t=0) 子树的复杂度为： 0.258 + 0.4 = 0.658

计算 R(t=5) 叶子结点的 CCP 复杂度， 0.722 * 5/14 + 0.1 = 0.358

Day,Weather,Temperature,Humidity,Wind,Play
1,Sunny,25,High,Weak,No
2,Sunny,24,High,Strong,No
3,Overcast,28,High,Weak,Yes
4,Rain,22,High,Weak,Yes
5,Rain,20,Normal,Weak,Yes
6,Rain,18,Normal,Strong,No
7,Overcast,21,Normal,Strong,Yes
8,Sunny,23,High,Weak,No
9,Sunny,19,Normal,Weak,Yes
10,Rain,24,Normal,Weak,Yes
11,Sunny,23,Normal,Strong,Yes
12,Overcast,26,High,Strong,Yes
13,Overcast,27,Normal,Weak,Yes
14,Rain,22,High,Strong,No

from sklearn.tree import DecisionTreeClassifier
import pandas as pd
from sklearn.tree import plot_tree
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings('ignore')


data = pd.read_csv('data-4.csv')
inputs = data[['Weather', 'Temperature', 'Humidity', 'Wind']]
labels = data['Play']
# 处理类别特征
inputs = pd.get_dummies(inputs)

estimator = DecisionTreeClassifier(criterion='entropy', ccp_alpha=0.2)
estimator.fit(inputs, labels)

plt.figure(figsize=(20, 15))
plot_tree(estimator,
          feature_names=list(inputs.columns),
          class_names=None,
          node_ids=True,
          precision=3,
          max_depth=None,
          fontsize=18,
          filled=True)
plt.show()

3. α 临界值

对于决策树中的每一个非叶子节点，计算其剪枝前和剪枝后的复杂度差值，如下公式所示：

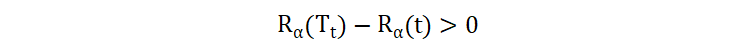
如果这个差值大于 0，说明剪枝之后能够降低整个决策树的复杂度。我们将该公式展开：

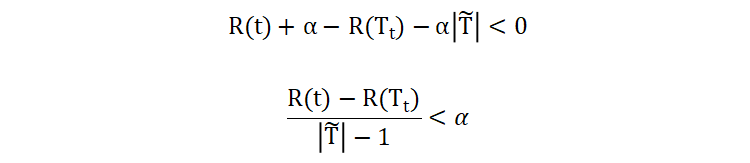
当 α 值大于左半部分的值时，就进行剪枝。即：左半部分值其实是一个临界 α 值，最大不剪枝的 α 值
α 值也表示平均不纯度的增加程度，即：剪掉某个子树之后决策树不纯度的增加程度

当有多个非叶子结点都满足剪枝条件时，一般选择 α 值最小的子树进行剪枝。原因是为了在最小的不纯度增加的代价下，实现模型的简化。

接下来，通过一个例子来理解 α 临界值的计算过程：

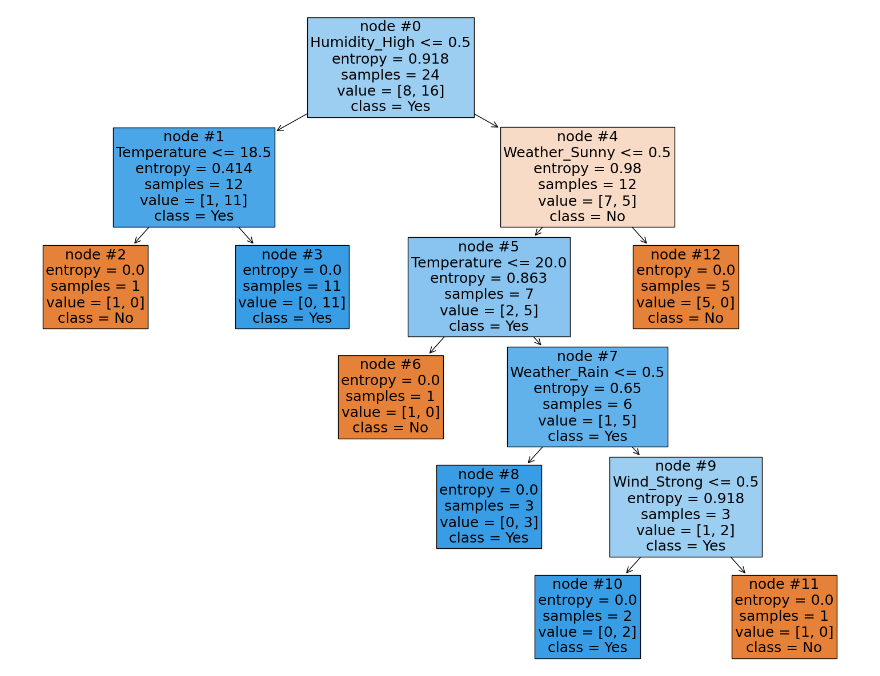
	node#1	node#4	node#5	node#7	node#9
\(R(t)\)	0.414*12/24	0.98*12/24	0.863*7/24	0.65*6/24	0.918*3/24
\(R(T_{t})\)	0	0	0	0	0
\(\|\tilde{T}\|\)	2	5	4	3	2
α 临界值	0.207	0.1225	0.0839	0.08125	0.11475

我们选择最小临界值 α= 0.08125 ，并设置 α 比该值稍微大一些。

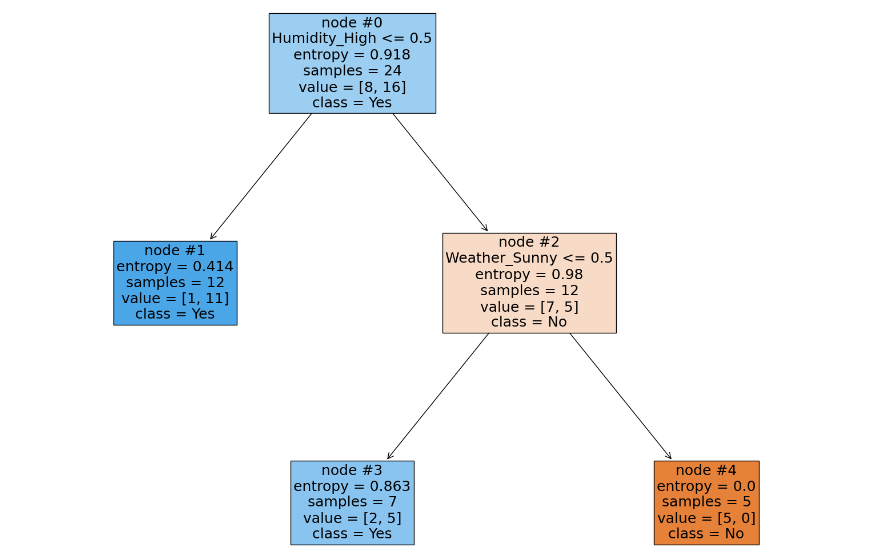
在剪枝之后，在新的树上，计算所有非叶子节点的剪枝代价，继续选择 α 最小的结点进行剪枝。当然，按照这种方式一直剪下去的话，无论多么复杂的决策树都会被剪成一个只有根节点的树桩，并且剪得越多，树的不纯度就越高，并且在剪枝的过程中也会获得多个 α 值，这些 α 值也组成了一个决策树的剪枝路径。

我们可以使用 from sklearn.tree import DecisionTreeClassifier 的 cost_complexity_pruning_path 函数来计算决策树的剪枝路径：

Day,Weather,Temperature,Humidity,Wind,Play
1,Sunny,25,High,Weak,No
2,Sunny,24,High,Strong,No
3,Overcast,28,High,Weak,Yes
4,Rain,22,High,Weak,Yes
5,Rain,20,Normal,Weak,Yes
6,Rain,18,Normal,Strong,No
7,Overcast,21,Normal,Strong,Yes
8,Sunny,23,High,Weak,No
9,Sunny,19,Normal,Weak,Yes
10,Rain,24,Normal,Weak,Yes
11,Sunny,23,Normal,Strong,Yes
12,Overcast,26,High,Strong,Yes
13,Overcast,27,Normal,Weak,Yes
14,Rain,22,High,Strong,No
15,Sunny,26,High,Strong,No
16,Sunny,22,Normal,Weak,Yes
17,Overcast,25,Normal,Strong,Yes
18,Rain,21,High,Weak,Yes
19,Sunny,24,High,Strong,No
20,Sunny,20,Normal,Weak,Yes
21,Rain,23,Normal,Weak,Yes
22,Overcast,24,High,Strong,Yes
23,Overcast,28,Normal,Weak,Yes
24,Rain,19,High,Strong,No

from sklearn.tree import DecisionTreeClassifier
import pandas as pd
from sklearn.tree import plot_tree
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings('ignore')



if __name__ == '__main__':

    # 读取训练数据
    data = pd.read_csv('data-3.csv')
    inputs = data[['Weather', 'Temperature', 'Humidity', 'Wind']]
    labels = data['Play']
    inputs = pd.get_dummies(inputs)

    # 训练完全增长的决策树
    estimator = DecisionTreeClassifier(criterion='entropy')
    estimator.fit(inputs, labels)

    # 计算每次剪枝的 ccp_alpha 临界值以及对应的不纯度值
    pth = estimator.cost_complexity_pruning_path(inputs, labels)
    print('ccp_alphas:', pth['ccp_alphas'])
    print('impurities:', pth['impurities'])

ccp_alphas: [0.         0.0812528  0.08923789 0.20690843 0.22982195]
impurities: [0.         0.16250561 0.2517435  0.45865192 0.91829583]

当选择的 α 值在 [0, 0.0812528] 时，整棵树的不纯度为 0
当选择的 α 值在 (0.0812528，0.08923789] 时，整棵树的不纯度为 0.16250561
当选择的 α 值在 (0.08923789，0.20690843] 时，整棵树的不纯度为 0.2517435
当选择的 α 值在 (0.20690843，0.22982195] 时，整棵树的不纯度为 0.45865192
当选择的 α 值在 (0.22982195，] 时，整棵树的不纯度为 0.91829583

至此，决策树的 CCP 剪枝算法就讲解完毕了，希望对你有所帮助。

代价复杂度剪枝（Cost-Complexity Pruning）

1. 剪枝原理

2. 复杂度计算

3. α 临界值

取消回复

文章目录