信息增益是决策树算法中用于特征选择的一个重要指标。在构建决策树时，我们需要确定哪个特征最能有效地分割数据，使得子节点的纯度最高。信息增益就是衡量这种分割能力的指标。
信息增益的计算基于信息熵（或熵）的概念。所以，我们需要了解熵的相关概念、计算方法，以及如何基于这些概念来构建分类决策树。
1. 信息熵
信息熵是信息论中一个重要的概念，由克劳德·香农在 1948 年引入，并被广泛应用于通信、数据压缩、统计学等领域，它是用于描述信息的不确定性、信息的容量、信息的不纯度。
- 信息的容量越大，信息的不确定性就越大
- 信息的容量越大，信息的不纯度（不单一）就越高
- 信息熵值越大，表示信息的容量就越大
如何去度量一个变量的信息熵？
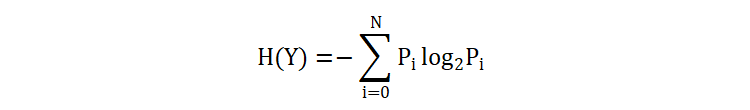
- \(N\) 表示变量 Y 中出现的值的种类
- \(P_i\) 表示第 i 类值出现的概率
假设：我们有变量 X 和 Y，其值如下表所示：
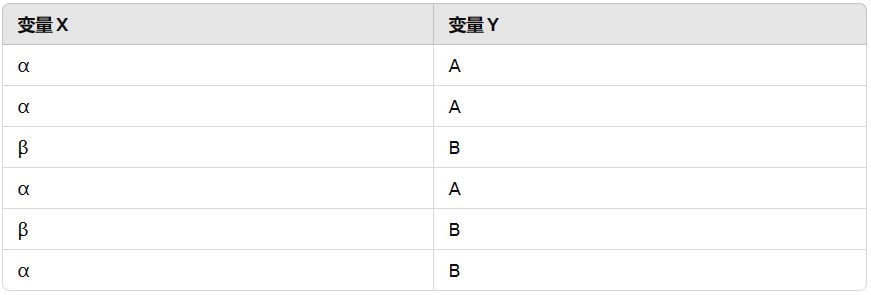
我们使用上述公式计算得到 X 和 Y 的信息熵如下：
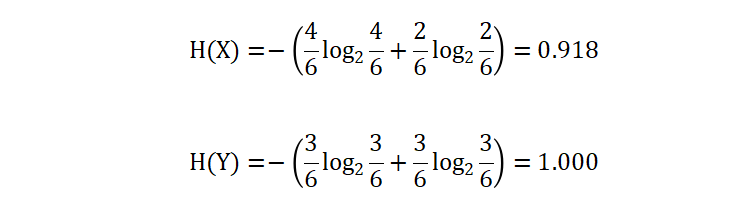
从计算结果也可以看到，变量 Y 信息熵大于变量 X，所以我们可以知道：
- 变量 Y 的不确定性、混乱程度、不纯度要高于变量 X
- 信息熵的大小与信息种类、信息出现的概率有关
2. 条件熵
条件熵 H(Y|X) 表示在已知随机变量 X 的条件下，随机变量 Y 的不确定性。结合下面的表，条件熵就是在某个特征作为条件的前提下，来计算目标值的熵值。
以特征 X 为条件，计算目标值 Y 的熵值。根据特征 X 将 Y 分为两部分：
- X = α 部分对应的目标值为： AAAB
- X = β 部分对应的目标值为： BB
条件 X=α 部分的信息熵：
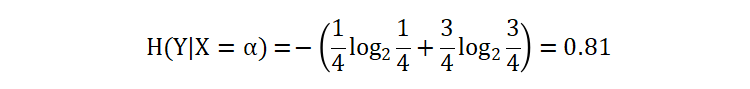
条件 X=β 部分的信息熵：
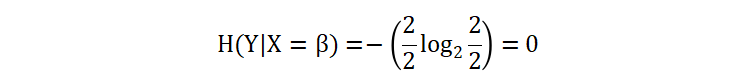
计算以 X 作为条件，目标值 Y 的条件熵值：
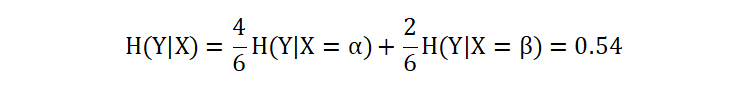
最终，计算得到在特征 X 的条件下，Y 的信息熵值为 0.54。
3. 信息增益
信息增益（Information Gain）描述了在知道一个特征的条件下，另外一个变量的不确定性、混乱程度、不纯度的减少量。具体地，给定一个特征 X 和变量 Y，信息增益 Gain(Y, X) 定义为：
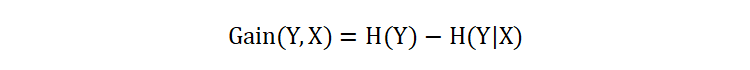
其中 H(Y) 是目标变量 Y 的信息熵，H(Y|X) 是在特征 X 的条件下 Y 的条件熵。
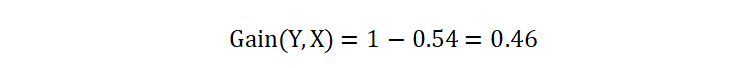
4. 决策树
我们通过一个例子，来了解如何基于信息增益来构建决策树。
| 序号 | 婚姻 | 收入(万) | 拖欠贷款 |
|---|---|---|---|
| 0 | 单身 | 6 | 否 |
| 1 | 已婚 | 8 | 否 |
| 2 | 单身 | 9 | 否 |
| 3 | 已婚 | 6 | 否 |
| 4 | 离异 | 7 | 是 |
| 5 | 已婚 | 9 | 否 |
| 6 | 离异 | 8 | 否 |
| 7 | 单身 | 6 | 是 |
| 8 | 已婚 | 6 | 否 |
| 9 | 单身 | 9 | 是 |
接下来，基于上面的数据集，使用信息增益来构建决策树。这里需要注意的是，我们使用的 scikit-learn 中的决策树 API 是无法直接处理类别特征数据，需要先将所有的类别特征进行独热编码（就是转换为数字），方便后续处理。
| 序号 | 婚姻_单身 | 婚姻_已婚 | 婚姻_离异 | 收入(万) | 拖欠贷款 |
|---|---|---|---|---|---|
| 0 | 1 | 0 | 0 | 6 | 否 |
| 1 | 0 | 1 | 0 | 8 | 否 |
| 2 | 1 | 0 | 0 | 9 | 否 |
| 3 | 0 | 1 | 0 | 6 | 否 |
| 4 | 0 | 0 | 1 | 7 | 是 |
| 5 | 0 | 1 | 0 | 9 | 否 |
| 6 | 0 | 0 | 1 | 8 | 否 |
| 7 | 1 | 0 | 0 | 6 | 是 |
| 8 | 0 | 1 | 0 | 6 | 否 |
| 9 | 1 | 0 | 0 | 9 | 是 |
我们将所有的特征的值升序排列：
| 婚姻_单身 | 婚姻_已婚 | 婚姻_离异 | 收入(万) |
|---|---|---|---|
| 0 | 0 | 0 | 6 |
| 1 | 1 | 1 | 7 |
| 8 | |||
| 9 |
取相邻两个数的均值作为切分点，如果有 N 个元素，则将会获得 N-1 个切分点：
| 婚姻_单身 | 婚姻_已婚 | 婚姻_离异 | 收入(万) |
|---|---|---|---|
| 0.5 | 0.5 | 0.5 | 6.5 |
| 7.5 | |||
| 8.5 |
我们先计算目标值的熵值，即：H(拖欠贷款)=0.881。
接着，计算每个切分点的条件熵值（每个切分点通过取 <= 和 >，将数据集划分为两部分）：
| 婚姻_单身=0.5 | 婚姻_已婚=0.5 | 婚姻_离异=0.5 | 收入(万)=6.5 | 收入(万)=7.5 | 收入(万)=8.5 | |
|---|---|---|---|---|---|---|
| 0.650 | 1.000 | 0.811 | 0.811 | 0.971 | 0.863 | |
| <= | 1 否 3 否 4 是 5 否 6 否 8 否 | 0 否 2 否 4 是 6 否 7 是 9 是 | 0 否 1 否 2 否 3 否 5 否 7 是 8 否 9 是 | 0 否 3 否 7 是 8 否 | 0 否 3 否 4 是 7 是 8 否 | 0 否 1 否 3 否 4 是 6 否 7 是 8 否 |
| 1.000 | 0.000 | 1.0 | 0.918 | 0.722 | 0.918 | |
| > | 0 否 2 否 7 是 9 是 | 1 否 3 否 5 否 8 否 | 4 是 6 否 | 1 否 2 否 4 是 5 否 6 否 9 是 | 1 否 2 否 5 否 6 否 9 是 | 2 否 5 否 9 是 |
| entropy | 0.790 | 0.600 | 0.849 | 0.875 | 0.846 | 0.880 |
| IG | 0.091 | 0.281 | 0.032 | 0.006 | 0.035 | 0.001 |
从计算结果来看，当使用特征 婚姻_已婚，并且选择 0.5 作为切分点时信息增益值最大，即：最大程度降低目标值的不确定性、混乱程度、不纯度。此时，我们分裂后的决策树如下：
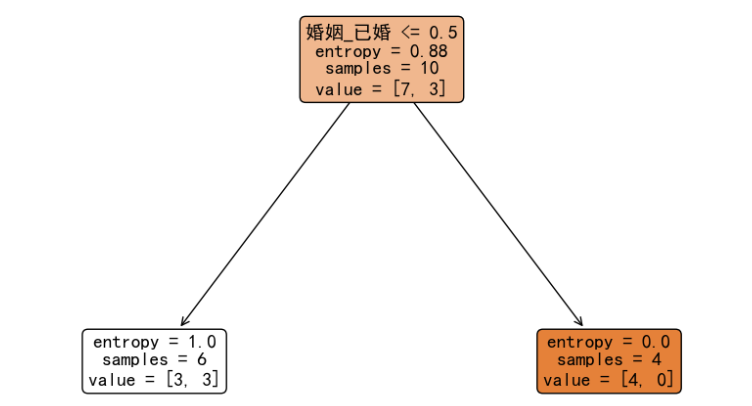
此时，我们发现右子树的信息熵值已经为 0，不需要再次分裂。左子树的信息熵值大于 0，所以需要继续进行分裂。我们继续计算基于左子树的 6 个样本的信息增益，选择能够最大程度降低不确定性的切分点继续分裂构造决策树。完整的决策树如下：
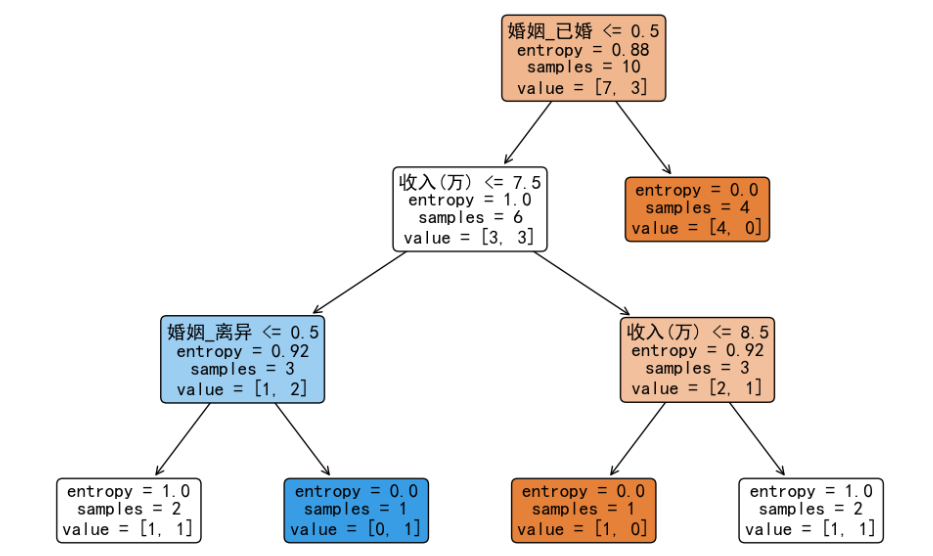
至此，关于使用信息增益构建决策树的内容就讲解完毕，希望对你有所帮助。
冀公网安备13050302001966号