线性回归(Linear Regression)是最基础的机器学习算法之一,用于建模因变量(目标变量)与一个或多个自变量(特征)之间的线性关系。它广泛应用于预测分析、统计建模和数据挖掘领域。


1. 决策函数
线性回归的核心是构建一个线性决策函数,以描述输入变量与输出变量之间的关系。线性回归的决策函数是一个线性组合,形式如下:
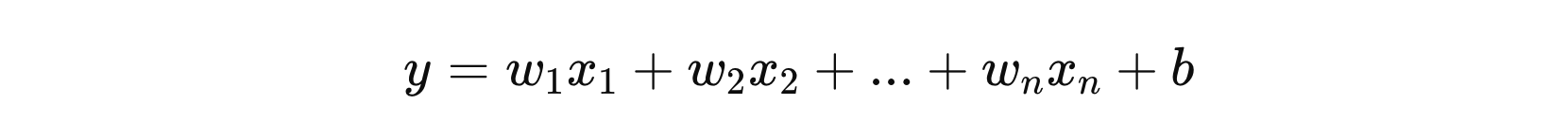
其中:
- \( x_{1}、x_{2} … x_{n} \) 表示输入变量
- \( w_{1}、w_{2} … w_{n} \) 表示权重参数
假设:有一个简单的线性回归模型,用于预测房价。经过对训练数据的学习,得到特征的权重分别为 \( w_{1} = 100 \) 和 \( w_{2} = 50 \),偏置 \( b = 20 \),则决策函数表示为:

对于一个面积 \( x_{1} = 120 \) 平方米、房间数量 \( x_{2} = 3 \) 的房屋,预测房价为:
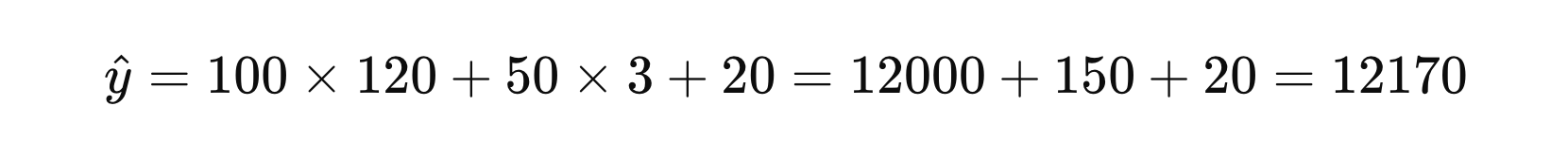
2. 损失函数
线性回归的损失函数通常使用 均方误差 (Mean Squared Error,MSE) 作为衡量模型预测与真实值差异的标准。其公式如下:
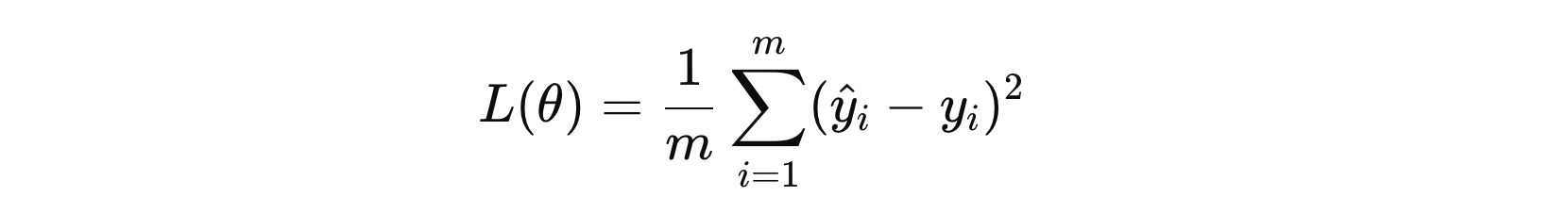
其中:
- \( m \) 表示样本的数量
- \( y_{i} \) 表示第 \( i \) 个样本的真实值
- \( \hat{y_{i}} \) 表示第 \( i \) 个样本的预测值
假设我们有以下数据:
以下是示例数据的表格展示:
| 样本编号 | 真实值 | 预测值 | 误差 | 误差平方 |
|---|---|---|---|---|
| 1 | 3 | 2.8 | -0.2 | 0.04 |
| 2 | 4 | 4.2 | 0.2 | 0.04 |
| 3 | 2 | 2.1 | 0.1 | 0.01 |
| 4 | 5 | 4.9 | -0.1 | 0.01 |
然后,损失函数计算如下:
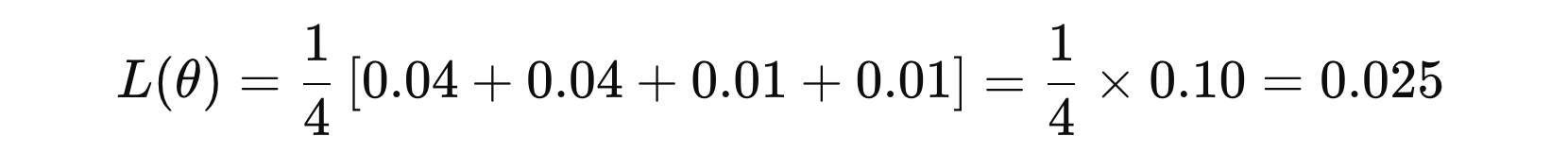
3. 优化方法
线性回归的优化方法主要是通过最小化损失函数(通常是均方误差,MSE)来找到最佳的模型参数。常见的优化方法包括:
- 正规方程法
- 梯度下降法
3.1 正规方程法
该优化方法直接基于训练数据计算参数,适用于小规模数据集。需要注意的是,正规方程法需要计算 \( X^{T}X \) 矩阵的逆。如果 \( X^{T}X \) 是奇异矩阵(即不可逆),正规方程法就不能得到解。在这种情况下,可能需要使用更复杂的方法来处理。
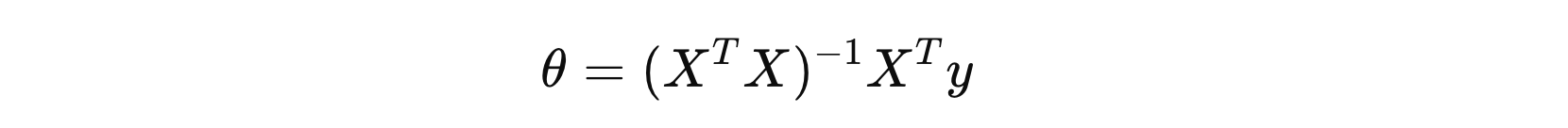
其中,\( X \) 表示输入数据矩阵,\( y \) 表示目标值,\( θ \) 表示参数。
3.2 梯度下降法
梯度下降法(Gradient Descent)是一种常用的优化算法,它通过迭代不断更新参数,以最小化损失函数,从而找到最优解。相比正规方程法,不需要像正规方程法那样计算 \( X^{T}X \) 的逆,避免了矩阵求逆的计算负担,适用于维度较高的问题。
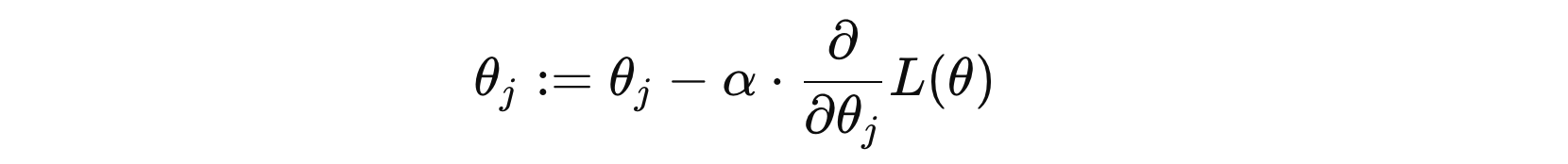
其中:
- \( θ_{j} \) 是模型参数
- \( α \) 表示学习率
- \( \frac{\partial}{\partial \theta_j} L(\theta) \) 是损失函数的对参数 \( θ_{j} \) 的偏导数
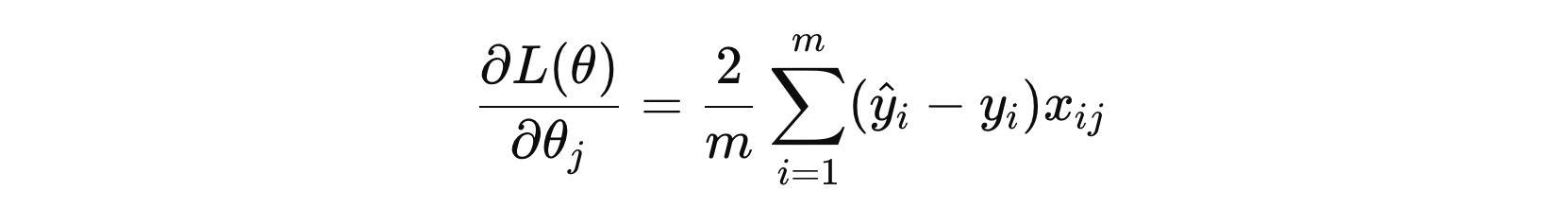

 冀公网安备13050302001966号
冀公网安备13050302001966号