SoftMax 函数是深度学习和机器学习中一个非常重要的概念，主要用于处理多分类问题。Softmax 函数能够将一个实数向量映射为一个概率分布，使得输出向量的所有元素都在 0 到 1 之间，并且它们的和为 1。

层次 Softmax（Hierarchical Softmax）是一种用于改进神经网络语言模型（如 Word2Vec 和 FastText）性能的技术。传统的 Softmax 在处理大量的类别时可能会非常慢，因为它需要对所有的类别进行指数运算和归一化。为了解决这个问题，研究人员提出了层次 Softmax 的概念。

1. 传统 SoftMax

Softmax 函数是一个将向量映射到概率分布的函数。计算公式如下：

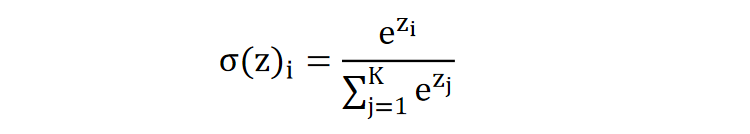
• \(σ(z)_{i}\) 表示 z 向量的第 i 个类别的概率
• \(z_{i}\) 表示向量 z 的第 i 个元素的值
• K 表示类别数量

从计算公式中，我们可以理解 Softmax 函数中涉及到对输入值进行指数计算、以及归一化计算。当类别数量很大时，会极大增加开销、复杂度，降低模型的训练效率。

2. 层次 SoftMax

层次 Softmax 通过构建一个层次结构（Huffman Tree），将类别映射到树的叶子节点，从而极大降低计算复杂度。

如何构建 Huffman Tree ？

假设：我们有四个类别 A、B、C、D ，权重分别为：5、7、2、13。

1. 将所有类别根据权重从小到大排列 (2 5, 7, 13) <==>(C、A、B、D)
2. 取出权重最小的两个类别，较小的作为左子结点，较大的作为右子结点
3. 两个类别权重的和作为父结点，并增加到列表中 (7, 7, 13) <==> (未知, B，D)
4. 重复 2-3 步，直到列表为空
5. 此时，霍夫曼树构建完成

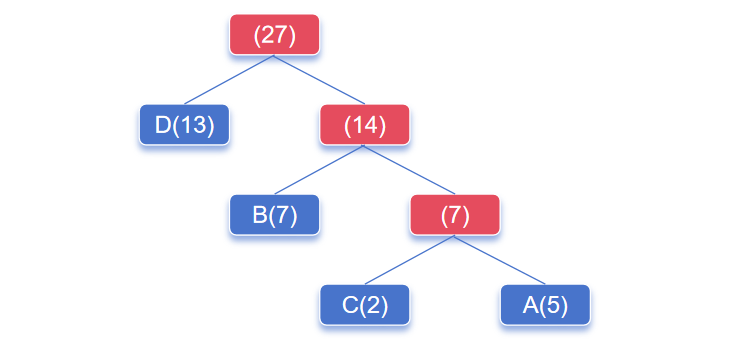
需要注意的是，上图构建的哈夫曼树中：

1. 每个非叶子节点都包含参数
2. 左节点为 0 类别，右节点为 1 类别

如何基于 Huffman Tree 获得每个类别的概率？

1. 输入向量与每一个非叶子结点参数计算得到分数
2. 通过使用 Sigmoid 函数计算每个分支的概率值

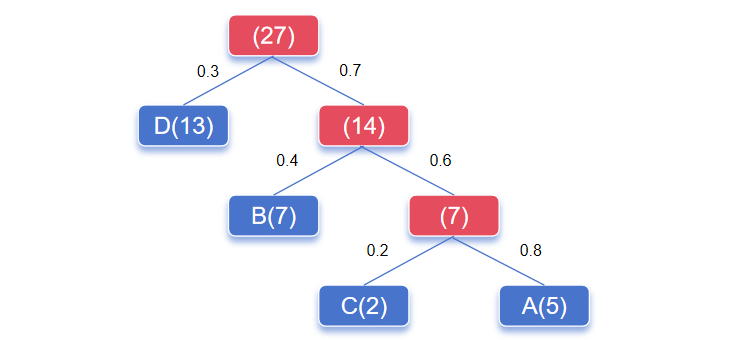
接下来，获得每个类别的概率值：

1. 每个类别的输出概率等于路径上的概率乘积，例如：C 的预测概率为：0.7 * 0.6 * 0.2 = 0.084
2. 所有叶子节点的预测概率和为 1
   • A 的预测概率：0.7 * 0.6 * 0.8 = 0.336
   • B 的预测概率：0.7 * 0.4 = 0.28
   • C 的预测概率：0.7 * 0.6 * 0.2 = 0.084
   • D 的预测概率：0.3
   • 0.336 + 0.28 + 0.084 + 0.3 = 1

最后需要注意的是：

1. 层次 Softmax 包含参数（即每个非叶子节点的参数向量），通常是通过训练过程来学习的。而标准 softmax 不包含参数。
2. 层次 softmax 适合输出类别较多的场景，而标准 softmax 适合输出类别较少的场景。

---

2024/10/22 同学提问更新

为啥层次softmax更快？

单从计算过程来看，层次softmax看起来并不比传统softmax计算量少多少。我们说的快，指的是在具体的某个场景下，比如：层次softmax是作为词向量训练过程中的优化算法。在词向量训练场景下，比如输入上下文词预测中心词，传统softmax需要对所有的词进行指数计算，才能得到中心词的概率。而层次softmax，则只需要计算路径上的概率值，只需要极少的指数计算，就可以得到中心词的预测概率，计算量大大减少了。这也是为什么说层次softmax更快的原因。我这么解释，可以理解吗？

为啥哈夫曼树的非叶子节点等于输出的维度？输出的维度不是由类别总数决定？

假设将算法部分的输出映射为一个概率分布。对于层次 softmax 而言，其概率计算需要得到树路径上的每一小段的概率值，而这小段的概率值的计算是算法的输出向量与每个非叶子节点的参数向量点积，再经过 sigmoid 得到。 如果非叶子节点的参数维度和算法输出维度不一样，就无法进行点积计算。