负采样（Negative Sampling）是一种优化策略，广泛用于词向量训练中，以降低计算复杂度并提高训练效率。本文将重点从词向量训练的角度，讲解负采样的背景问题、优化思路及其实际效果。

1. 问题场景

在训练词向量时，Skip-Gram 模型的目标是学习词的分布表示（输入上下文词来预测中心词），使得相近的词具有相似的向量表示。其核心思想是输入某个中心词来预测其周围的上下文词（context words）。

假设：给定一个句子 “The cat sits on the mat”，目标是训练词向量，使得 cat 能正确预测其上下文词 the 和 sits。Skip-Gram 采用最大化共现词对的概率的方法来训练词向量，该概率由 softmax 函数计算：

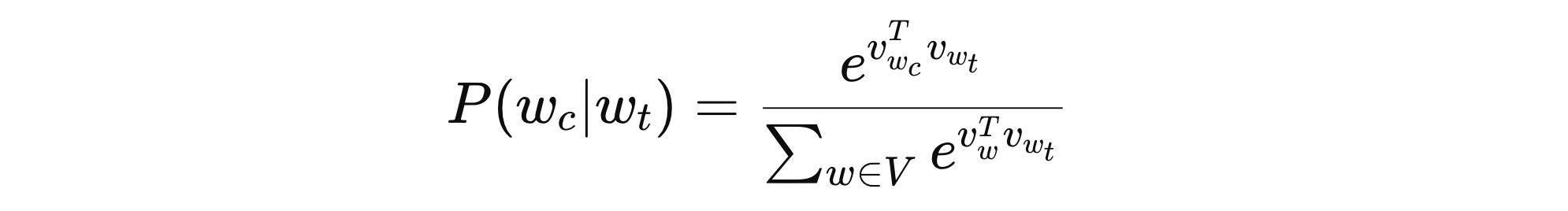
其中：

• \( V \) 表示整个词表
• \( w_{t} \) 表示中心词
• \( w_{c} \) 表示上下文词
• \( v_{w} \) 表示 \( w \) 的词嵌入向量

问题：这个公式涉及整个词汇表的归一化计算，当词汇表很大（比如百万级别）时，计算 softmax 代价极高。

2. 优化思路

我们还以前面的为例，Skip-Gram 训练的目标是让中心词 cat 能够预测其真实上下文词 the 和 sits，我们把这条数据整理为如下两条正样本：

• (cat, the)
• (cat, sits)

词汇表 V = {the, cat, sits, on, mat, dog, runs}，负采样策略是从整个词汇表中随机选取一些非上下文词作为负样本。假设我们选择 k=2 个负样本，由于 dog 和 runs 没有出现在 cat 的上下文中，我们就用这两个词构造两个负样本：

• (cat, dog)
• (cat, runs)

Skip-Gram 使用负采样进行训练，我们不使用 softmax 计算整个词汇表的概率，而是采用 sigmoid 函数计算每个词对的共现概率。

• 对于正样本计算，我们希望 cat 与 the、sits 的共现概率最大，目标是让这些值接近 1
• 对于负样本计算，我们希望 cat 与 dog、runs 的共现概率最小，目标是让这些值接近 0

简言之：我们要最大化正样本的共现概率，同时最小化负样本的共现概率。损失计算可以用下面的公式：

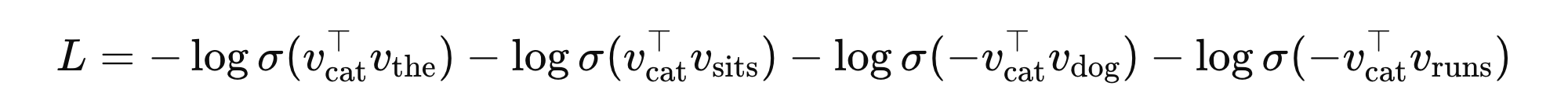
\( v_{cat} \)、\( v_{the} \)、\( v_{dog} \)、\( v_{runs} \) 表示对应词的向量表示。

3. 优缺点

负采样的优点主要体现在计算效率、内存消耗和训练速度上。通过避免对整个词汇表计算 softmax，负采样只需要处理少量的负样本，从而显著降低了计算复杂度，尤其适用于大规模数据集。此外，负采样不需要存储整个词汇表的概率分布，减少了内存占用，进一步提高了模型的效率。同时，由于减少了计算量，训练过程得以加速。

然而，负采样也存在一些缺点。首先，负样本的随机选择可能导致某些负样本缺乏足够的区分性，从而影响模型的性能。其次，负采样无法完全捕捉词汇之间的全局信息，可能导致词向量的精度低于使用整个词汇表计算的精确度。最后，负样本的数量（k）作为超参数需要调整，选择过多或过少都会影响训练效果，增加了调参的复杂度。

总的来说，负采样是一种高效的优化策略，特别适用于大规模数据集，能够显著提高训练速度并降低计算资源消耗。然而，它在模型精度和全局信息捕捉方面存在一定的限制，不如使用整个词汇表进行计算的全局方法精确。