在机器学习和统计学中，核函数（Kernel Function）是一种用于通过一种巧妙的方式将数据映射到高维空间的技术，从而使得在这个高维空间中，数据变得线性可分。它广泛应用于支持向量机（SVM）、主成分分析（PCA）、高斯过程等算法中。核函数的核心思想是避免直接进行高维映射的复杂计算，而是通过核技巧（Kernel Trick）在低维空间中进行计算，极大地提高了计算效率。

1. 核函数计算

核函数本质上是一个计算内积的函数。对于两个输入向量 \( x \) 和 \( y \)，核函数 \( K(x, y) \) 计算的是它们在某个隐含的高维空间中的内积。我们可以通过核函数来避免直接进行高维映射的计算，从而节省计算资源和时间。

常见的核函数包括线性核、多项式核、高斯核（RBF核）、Sigmoid核等，以及用户自定义的核函数。选择适当的核函数取决于数据的性质和问题的需求。核函数的使用允许机器学习模型处理更加复杂的问题，提高了分类和回归任务的性能。

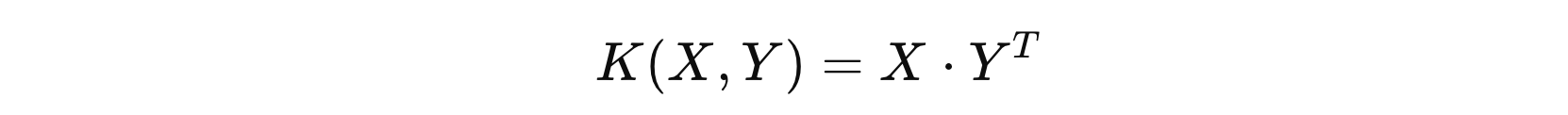
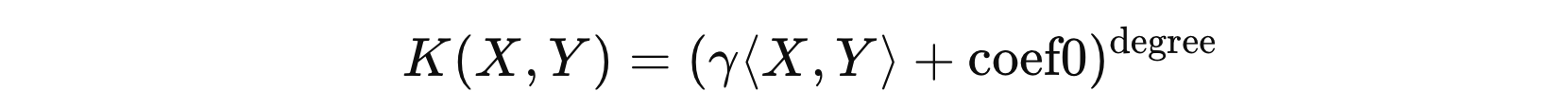
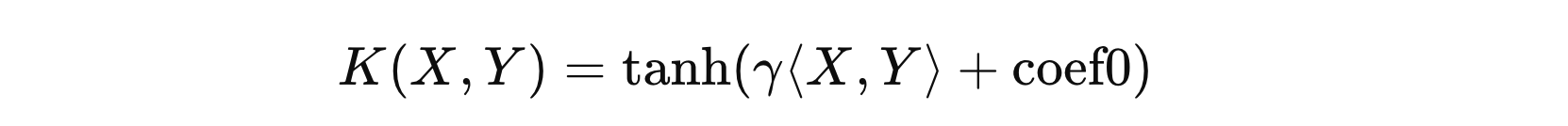
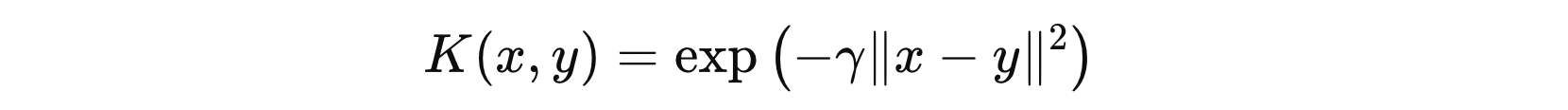
其中：

\( \langle X, Y \rangle \) 表示 \( X \) 和 \( Y \) 的内积
\( \gamma \) 表示可调参数
\( coef0 \) 表示常数项
\( degree \) 表示多项式的阶数

下面相关的 API 的使用和计算过程：

import math
from sklearn.metrics.pairwise import rbf_kernel
from sklearn.metrics.pairwise import polynomial_kernel
from sklearn.metrics.pairwise import sigmoid_kernel
from sklearn.metrics.pairwise import linear_kernel
import numpy as np


np.random.seed(0)
x = np.random.randint(0, 5, (2, 3))
print(x)

"""
[
    [4 0 3]
    [3 3 1]
]
"""

# 1. 线性核函数
# K(X, Y) = X @ Y.T
def test01():
    # [[25. 15.]
    #  [15. 19.]]
    kernel_matrix = linear_kernel(x)
    print(kernel_matrix)

    # [[25. 15.]
    #  [15. 19.]]
    kernel_matrix = x @ x.T
    print(kernel_matrix)


# 2. 多项式核函数
# K(X, Y) = (gamma <X, Y> + coef0) ^ degree
def test02():
    # [[42.875 15.625]
    #  [15.625 24.389]]
    kernel_matrix = polynomial_kernel(x, degree=3, gamma=0.1, coef0=1)
    print(kernel_matrix)

    # [[42.875 15.625]
    #  [15.625 24.389]]
    kernel_matrix = (0.1 * x @ x.T + 1) ** 3
    print(kernel_matrix)


# 3. Sigmoid核函数
# K(X, Y) = tanh(gamma <X, Y> + coef0)
def test03():
    # [[1. 1.]
    #  [1. 1.]]
    kernel_matrix = sigmoid_kernel(x, gamma=2, coef0=3)
    print(kernel_matrix)

    # [[1. 1.]
    #  [1. 1.]]
    kernel_matrix = np.tanh(2 * x @ x.T + 3)
    print(kernel_matrix)


# 4. 高斯核函数
# K(x, y) = exp(-gamma ||x-y||^2)
def test04():
    # [[1.00000000e+00 6.91440011e-13]
    #  [6.91440011e-13 1.00000000e+00]]
    kernel_matrix = rbf_kernel(x, gamma=2)
    print(kernel_matrix)

    # [[1.00000000e+00 6.91440011e-13]
    #  [6.91440011e-13 1.00000000e+00]]
    # 计算两两行之间的差值
    row_diff = x[:, np.newaxis] - x
    print(np.exp(np.sum(-2 * row_diff ** 2, axis=-1)))


if __name__ == '__main__':
    test04()

2. 核函数选择

选择合适的核函数并不是一件简单的事，它依赖于多个因素，包括数据的特性、问题的复杂性以及计算效率等。以下是一些选择核函数时的标准：

根据数据的线性可分性。当数据本身就是线性可分时，线性核函数通常是最优选择。线性核函数的计算开销较小，且能有效地拟合数据。线性核函数能够直接计算数据点的内积，因此当数据在原始空间中线性可分时，使用线性核能够获得最好的性能。如果数据本身是非线性可分的，我们通常需要使用更复杂的核函数，例如多项式核函数或 RBF 核函数。RBF 核函数尤其适用于复杂的非线性问题，它能够在高维空间中为数据点创建更加灵活的分隔面。

从数据数据维度的角度。如果数据本身就已经在一个高维空间中，例如图像数据或文本数据，可能不需要将数据进一步映射到更高的维度。在这种情况下，使用线性核函数通常就足够了。因为高维数据本身已经具备较好的分隔性。对于低维数据，尤其是特征之间有较强非线性关系的情况，使用 RBF 核或多项式核函数可能会更合适。这些核函数能够通过非线性映射将数据映射到高维空间，从而增强其可分性。

不同的核函数有不同的超参数需要调节。例如，RBF 核函数的参数 \( \gamma \) 控制数据点之间的相似度，过小的 \( \gamma \) 会导致模型过于简单，过大的 \( \gamma \) 会导致模型过拟合。相比之下，线性核函数通常不需要调节超参数，因此其调参过程较为简单。

虽然以上标准能够帮助我们做出一些指导性的选择，但最终的核函数选择仍然依赖于问题的具体情况和实验结果。以下是一些选择核函数的实际步骤：

步骤1：根据数据的特性选择初步的核函数。如果数据看起来线性可分，可以首先尝试线性核函数；如果数据具有复杂的非线性关系，则可以选择 RBF 或多项式核函数。
步骤2：调整模型的超参数。例如，对于 RBF 核函数，调节 \( \gamma \) 参数；对于多项式核函数，调整 \( \gamma \)、\( coef0 \) 和 \( degree\)。使用交叉验证等技术来选择最佳的参数。
步骤3：进行模型评估。通过交叉验证、网格搜索等方法评估不同核函数的性能，选择最佳的核函数。

最后，选择核函数并没有绝对的标准，重要的是要根据具体问题进行试验与调优，从而找到最适合的解决方案。

3. 核函数使用

在 scikit-learn 中，以下算法都支持核函数的应用。

from sklearn.decomposition import KernelPCA
from sklearn.kernel_ridge import KernelRidge
from sklearn.svm import SVC
from sklearn.svm import SVR
from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process import GaussianProcessClassifier
from sklearn.cluster import SpectralClustering

PCA 通常用于线性降维，但在非线性情况下，数据可能不能通过线性方法有效地分离。Kernel PCA 使用核方法将数据映射到高维特征空间，在高维空间中执行 PCA，从而更好地找到数据的主成分。

普通的 Rigge 是线性模型，但在很多实际问题中，数据可能呈现非线性关系。核岭回归利用核函数将数据映射到高维空间，解决非线性问题。

SVC 本身是为线性分类设计的，但现实中许多问题是非线性的。通过核函数，SVC可以在高维空间中找到非线性决策边界，从而更好地分类数据。

高斯过程是一种非参数化方法，用来处理复杂的非线性回归问题。核函数定义了模型的平滑度和假设的非线性关系，因此它能够捕捉到数据中的非线性模式。

谱聚类本质上是基于图的聚类方法，而图的结构依赖于数据点之间的相似性度量。通过使用核函数，谱聚类能够更好地捕捉到数据的非线性结构和复杂的聚类关系。

核函数（Kernel Function）

1. 核函数计算

2. 核函数选择

3. 核函数使用

取消回复

文章目录