《手写数字识别》项目基于支持向量机算法的，该算法的背后有着坚实的数学理论作为支撑，为算法的有效性和可靠性提供了坚实的基础。接下来，我们将会从以下第五个方面来讲解：

1. 算法思想初探
2. 算法训练内容
3. 算法推理过程
4. 惩罚参数作用
5. 核函数的作用

1. 算法思想初探

一共有 13 个样本（二维向量）， 6 个红色的、7 个黑色的，其在空间中的分布如下：

我们的目标是在该空间中找到一条直线（超平面）将黑色和红色类别样本正确分类。但是，满足能够进行正确分类的直线就会存在很多中，如下图所示：

我们究竟如何选择这一条直线，或者说哪一条直线会更好？

为了能够对未知样本的泛化能力更强一些，我们倾向于选择 B 直线作为分类平面。如下图所示：

原因是：SVM 认为 B 直线能够在样本分类正确的情况，并且距离两个类别样本最远，这样使得在预测未知样本时，能够使其更加接近其真实类别。

至此，我们得出支持向量机的目标：

在训练时，将所有样本分类正确的前提下，寻找一个超平面距离两个类别的样本距离最大。

2. 算法训练内容

对于分类超平面 B, 我们可以用下面的公式来表示（需要确定的是，斜率 w，截距 b）：

其中 w 可以用以下公式计算得到：

上述公式中的 x 表示支持向量，而 α 表示支持向量的系数，y 表示支持向量的标签（-1或+1）。

偏置 b 可以用以下公式计算得到：

所示，支持向量机分类超平面的确定由支持向量以及其系数来确定的。如下图，支持向量 P 和 O 共同确定最大的间隔的两个边界，从而得到分类超平面 B。

支持向量：就是一组落在最大间隔边界上的样本，这些样本支撑着最大间隔构建。

现在，那我们就清楚了，在支持向量机训练过程中，就是要根据训练集数据计算得到在样本分类正确，并且间隔最大化的支持向量以及其系数。由此，就可以得到支持向量机的参数 w 和 b。

补充：支持向量的系数是 >= 0 的值，如果样本非支持向量，则其对应系数为 0，否则为非 0。

3. 算法推理过程

当我们拿到一个未知的样本，想对你进行分类，那么就让该样本计算和所有支持向量的相似度，从而得到一个分数，如何这个分数小于等于 0，就将其归类为 -1 类别，否则将其归类于 +1 类别。

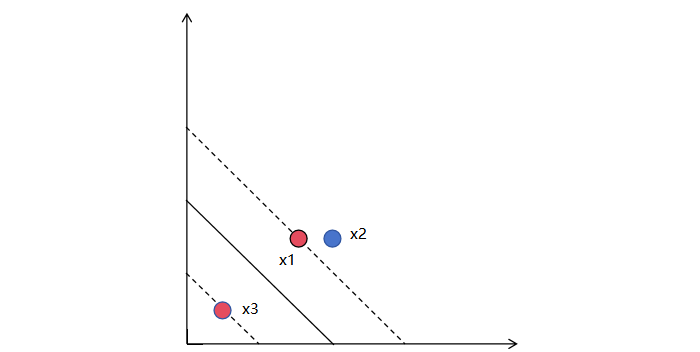
正负样本的支持向量如下

x1 = (3, 3)，y1 = +1，系数 1/4
x3 = (1, 1)，y3 = -1， 系数 1/4
b = -2

待预测的未知样本为：x2 = (4, 3)

4. 惩罚参数作用

硬间隔指在样本分类正确的情况下，寻找间隔最大化的分类超平面。如果出现异常值、或者样本分布比较复杂，此时硬间隔无法实现。

软间隔指的是我们容忍一部分样本在最大间隔之内，甚至在错误的一边。这样使得支持向量机能够更加适合实际的问题场景。

在硬间隔的情况下，我们只考虑如何使得间隔达到最大。在软间隔的情况，我们即要考虑最大化间隔，也要考虑到那些限制间隔违例的样本带来的影响。

间隔违例和最大间隔的相互影响是什么？

间隔较大，模型的泛化能力相对就越好。间隔违例越多，模型可能会出现欠拟合。如果容忍更多间隔违例将会获得更大的间隔，模型的泛化能力可能能够有所提升。如果容忍较少的间隔违例，相对获得最大间隔就会较小，模型的泛化能力较弱。

在支持向量机训练过程中，是需要平衡这两部分。

支持向量机是通过对间隔违例样本进行惩罚的方式来实现平衡。惩罚参数一般用 C 来表示，它是是超参数，能够左右间隔违例样本的带来的负面影响。C 实际是间隔违例样本前面乘以的系数，可以放大或者减小间隔违例样本的影响。

1. C 越大说明，违反限制间隔的样本点带来的影响就越大，就要减少这些样本的数量，所以间隔就要越小。

2. C越小说明，违反限制间隔的样本点带来的影响就越小，可以适当增大间隔，以增加模型的泛化能力。

简言之：

C 值可以用来平衡训练过程中间隔违例样本损失、最大间隔。当对违反限制间隔的样本点的容忍度很低时，可增大C值，反之可减少C值。

5. 核函数的作用

核函数是一种用于支持向量机和一些其他机器学习算法的数学函数，它的作用是将数据从原始特征空间映射到一个更高维度的特征空间。

核函数的主要目的是使原本在低维特征空间中线性不可分的数据在新的高维特征空间中变得线性可分，从而更容易找到一个线性决策边界来分隔不同类别的数据点。

当支持向量机碰到的问题较为复杂，即当数据分布复杂、无法做到线性可分的时候，我们可以 通过将数据映射到更高维的特征空间，从而有更多的可能性找到一个超平面来分割不同类别的数据点。

如何理解将数据映射到高维空间，能够实现线性可分？

1. 在低维空间中，数据点分布可能会相对靠近，但当它们被映射到高维空间时，它们在更大的空间中分布可能会变得更分散，数据点可能呈现出更多的结构和分布，使得呈现更多的线性可分的可能。
2. 当我们将数据从低维空间映射到高维空间时，引入了额外的特征维度，包含更多信息。这些额外的维度使得数据在高维空间中更丰富，更具多样性。

简言之：核函数通过将样本投射到高维空间，数据样本在高维空间中的分布会发生变化，从而有更多的可能性寻找到更好的分类超平面。

在训练时，我们就需要通过核函数将所有的训练样本投射到高维空间，并且在高维空间中寻找支持向量以及其系数。在推理时，也需要将未知样本投射到高维空间再预测确定样本的类别。

最后，需要补充一个重要的点：

核函数并不实际进行数据投射或计算高维特征空间中的特征向量，它使用数学函数来度量数据在高维特征空间中的相似性，而不需要实际将数据映射到高维空间中。所以，核函数也被称作核技巧。