伯努利朴素贝叶斯（Bernoulli Naive Bayes）分类器是一种基于贝叶斯定理的概率分类器，常用于处理文本分类等离散数据。它假设特征之间是条件独立的，并且每个特征都遵循伯努利分布，即每个特征只有两个可能的取值（通常是0和1，表示特征是否出现）。

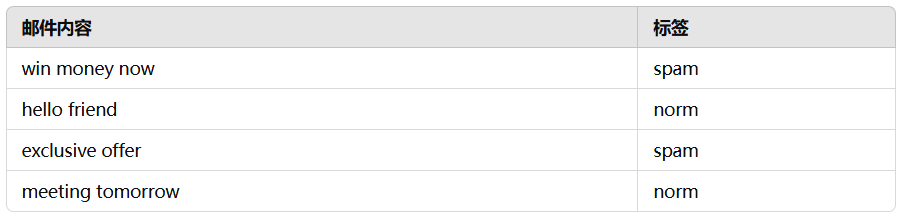
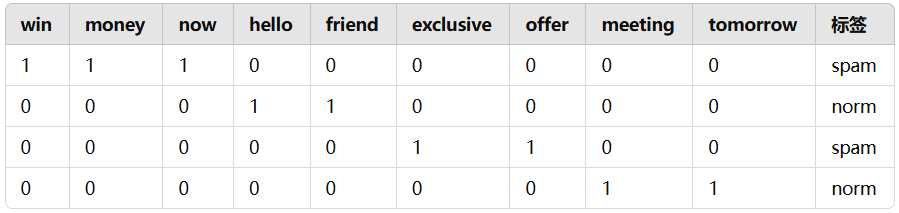
win,money,now,hello,friend,exclusive,offer,meeting,tomorrow,Spam
1,1,1,0,0,0,0,0,0,1
0,0,0,1,1,0,0,0,0,0
0,0,0,0,0,1,1,0,0,1
0,0,0,0,0,0,0,1,1,0

1. 伯努利分布

伯努利分布是一种离散概率分布，用于描述一个只有两个可能结果的随机试验。这两个结果通常被标记为 “成功”（记为1）和”失败”（记为0），并且成功的概率记为 p，失败的概率则为 1−p。

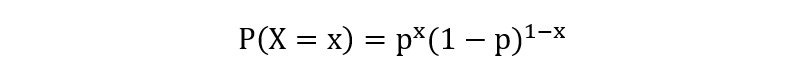
• \(p\) 是成功的概率， \(0 \leq p \leq 1\)
• x 是随机变量 X 的取值（0 或 1）

2. 训练过程

对于朴素贝叶斯算法，训练过程就是在根据训练数据，统计每个特征值的在类别条件下的概率，以及类别的先验概率。

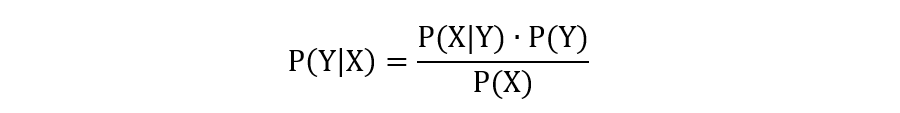
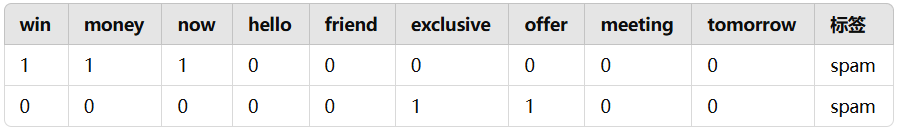
在伯努利朴素贝叶斯中，假设每个特征值服从伯努利分布。对于特征 x 在类别 y 条件下的概率计算，可以表示为：

公式中的 α 为拉普拉斯平滑系数，避免出现为 0 的情况，默认值为 1。训练得到的内容如下：x = 1 的条件概率：

3. 预测过程

待预测的邮件内容： “win hello” ，二值向量表示：

3.1 计算 spam 分数

计算联合条件概率：

\(P(spam)·P(win=1∣spam) ⋯ P(tomorrow=0∣spam)\)

转换为联合对数概率计算（避免数值溢出）：

\(log(P(spam)) + log(P(win=1∣spam)) + ⋯ +log(P(tomorrow=0∣spam))\)

代入样本计算最后的结果：

\(log(0.5) + log(0.5) + log(0.5) + log(0.5) +log(0.25) + \\log(0.75) + log(0.5) +log(0.5) + log(0.75) + log(0.75) = -6.40822366\)

3.2 计算 norm 分数

计算联合条件概率：

\(P(norm)·P(win=1∣norm) ⋯ P(tomorrow=0∣norm)\)

转换为联合对数概率计算：

\(log(P(norm)) + log(P(win=1∣norm)) +⋯ +log(P(tomorrow=0∣norm))\)

代入样本计算最后的结果：

\(log(0.5) + log(0.25) + log(0.75) + log(0.75) +log(0.5)+\\log(0.5)+log(0.75)+log(0.75)+log(0.5)+log(0.5) =-6.00275855 \)

由于 \(-6.00275855 > -6.40822366\)，所以该邮件为 norm。

4. API 使用

from sklearn.naive_bayes import BernoulliNB
import numpy as np
import pandas as pd
import warnings
warnings.filterwarnings('ignore')


if __name__ == '__main__':

    data = pd.read_csv('data.csv')

    # 训练
    # alpha 平滑系数
    # binarize 二值化阈值
    estimator = BernoulliNB(alpha=1,  binarize=0.0)
    estimator.fit(data.iloc[:, :-1], data.iloc[:, -1])


    print('对数先验概率:\n', estimator.class_log_prior_)
    print('对数条件概率(值=1):\n',estimator.feature_log_prob_)

    # 预测
    new = np.array([[1, 0, 0, 1, 0, 0, 0, 0, 0]])
    scores = estimator.predict_joint_log_proba(new)

    print('类别分数:', estimator.classes_, scores.squeeze())

程序执行结果：

对数先验概率:
 [-0.69314718 -0.69314718]

对数条件概率(值=1):
 [[-1.38629436 -1.38629436 -1.38629436 -0.69314718 -0.69314718 -1.38629436
  -1.38629436 -0.69314718 -0.69314718]
 [-0.69314718 -0.69314718 -0.69314718 -1.38629436 -1.38629436 -0.69314718
  -0.69314718 -1.38629436 -1.38629436]]

类别分数: [0 1] [-6.00275855 -6.40822366]