高斯朴素贝叶斯(Gaussian Naive Bayes)是一种基于贝叶斯定理的分类算法,它假设数据的特征遵循高斯(正态)分布,属于朴素贝叶斯分类器的一种。
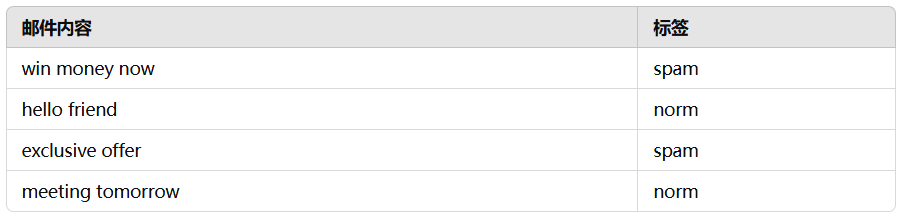
我们可以基于词频、TF-IDF、Word2Vec 等方法将邮件内容转换为向量表示。
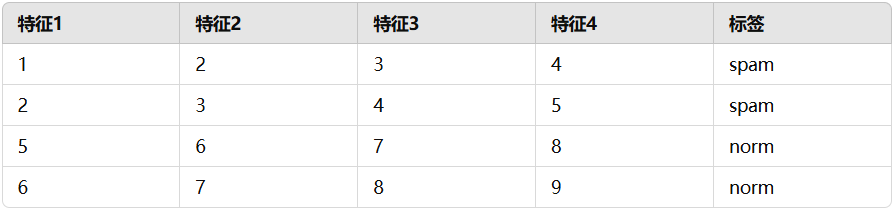
1. 高斯分布
高斯分布,也称为正态分布,是统计学中最常见的概率分布之一,它在自然界和社会现象中都有着广泛的应用。高斯分布的形状呈钟形曲线,其特点是均值(μ)确定了曲线的中心位置,标准差(σ)确定了曲线的宽度。
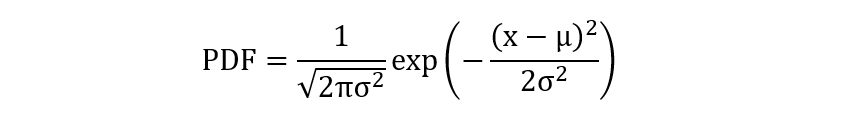
- \(\mu\) 表示某个特征 x 在类别 y 条件下的均值
- \(\sigma^2\) 表示某个特征 x 在类别 y 条件下的方差
- 公式表示了在给定分布参数下,某个值出现的相对可能性大小
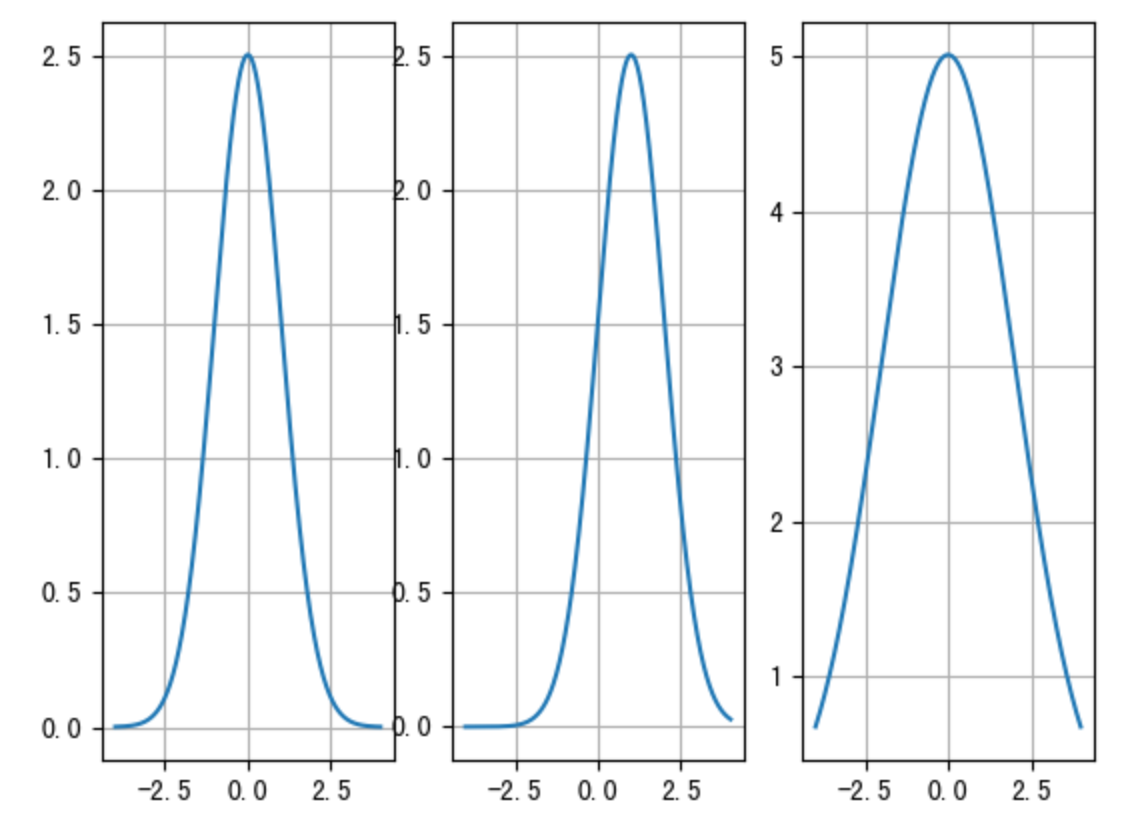
高斯分布中,均值决定了图像的位置,均值较大相对靠右,均值较小,相对靠左。方差决定了分布范围,方差越大,则分布范围越大,方差越小分布范围就越集中。
2. 训练过程
朴素贝叶斯的训练过程最重要的是得到每个特征值的条件概率、类别特征的先验概率。对于服从高斯分布的每个特征,只要在训练时,得到类别条件下的每个特征的均值和方差,即可得到当该特征取某值时的条件概率。
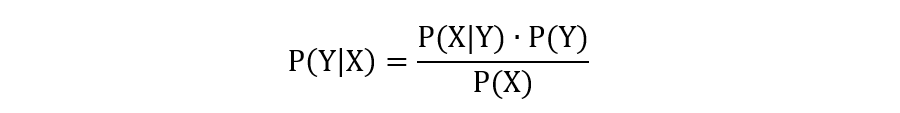
2.1 spam 均值和方差

训练得到的 spam 类别下的各个特征的均值和方差:
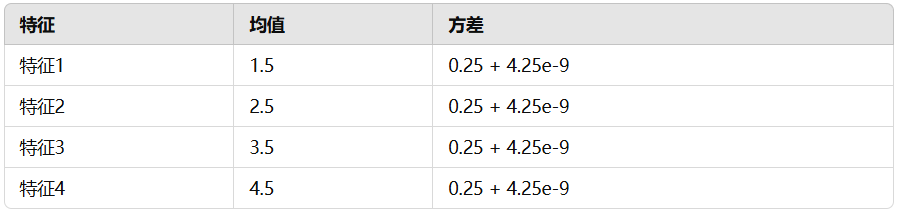
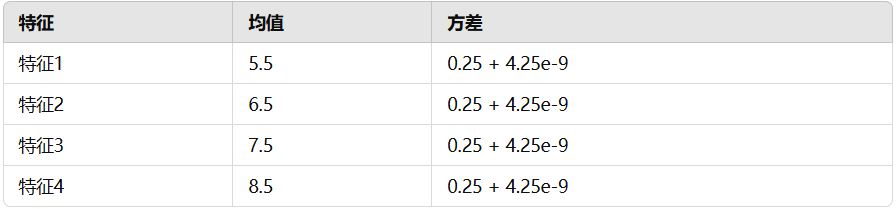
2.2 norm 均值和方差

训练得到的 norm 类别下的各个特征的均值和方差:
需要注意的是,方差有可能出现为 0 的情况,所以这里需要对方差的计算做一个平滑处理,在 scikit-learn 的实现中,平滑的计算公式:
# self.var_smoothing 为超参数,默认值 1e-9 # np.var(X, axis=0) 计算输入数据集每个特征的方差 self.epsilon_ = self.var_smoothing * np.var(X, axis=0).max() # 每个特征的方差减去平滑系数 self.var_[:, :] -= self.epsilon_
在一些特征取值较为稀疏或类别分布不均衡的情况下,epsilon_ 提供了一种平滑效果,使模型对这些特征和类别的处理更加鲁棒,避免过拟合或过度依赖某些特征。
3. 预测过程
假设:我们有一个新的邮件内容,经过向量化之后如下:

3.1 计算 spam 分数
计算联合条件概率:
\(P(spam)·P(特征1=3.5∣spam) ⋯ P(特征4=7.2∣spam)\)转换为联合对数概率计算(避免数值溢出):
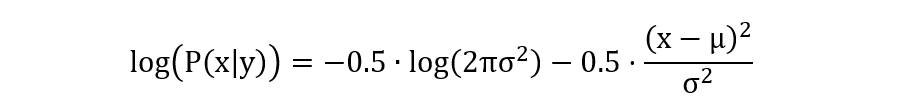
- \(log(P(spam)) = log(0.5)=-0.6931471805599453\)
- \(log(P(特征1=3.5|spam)) =-8.225791225144729\)
- \(log(P(特征1=6.5|spam)) =-32.225790817144734\)
- \(log(P(特征1=1.1|spam)) =-11.74579116530473\)
- \(log(P(特征1=7.2|spam)) =-14.805791113284732\)
- 计算分数:\(-67.69631150143887\)
3.2 计算 norm 分数
计算联合条件概率:
\(P(norm)·P(特征1=3.5∣norm) ⋯ P(特征4=7.2∣norm)\)转换为联合对数概率计算(避免数值溢出):
- \(log(P(norm)) = log(0.5)=-0.6931471805599453\)
- \(log(P(特征1=3.5|norm)) =-8.225791225144729\)
- \(log(P(特征1=6.5|norm)) =-0.22579136114472736\)
- \(log(P(特征1=1.1|norm)) =-82.14578996850476\)
- \(log(P(特征1=7.2|norm)) =-3.605791303684727\)
- 计算分数:\(-94.89631103903889\)
由于 \(-67.69631150143887 > -94.89631103903889\),所以该邮件为 spam。
4. API 使用
from sklearn.naive_bayes import GaussianNB
import numpy as np
if __name__ == '__main__':
inputs = np.array([[1, 2, 3, 4],
[2, 3, 4, 5],
[5, 6, 7, 8],
[6, 7, 8, 9]], dtype=np.float32)
print(inputs)
labels = np.array([0, 0, 1, 1])
estimator = GaussianNB()
estimator.fit(inputs, labels)
# 每个特征的均值
print('特征均值:\n' + str(estimator.theta_))
# 每个特征的方差
print('特征方差:\n' + str(estimator.var_))
# 平滑系数
print('方差平滑:', estimator.epsilon_)
# 先验概率
print('先验概率:', estimator.class_prior_)
# 数据预测
y_pred = estimator.predict_joint_log_proba(np.array([[3.5, 6.5, 1.1, 7.2]]))
print('预测标签:', y_pred)
程序输出结果:
[[1. 2. 3. 4.] [2. 3. 4. 5.] [5. 6. 7. 8.] [6. 7. 8. 9.]] 特征均值: [[1.5 2.5 3.5 4.5] [5.5 6.5 7.5 8.5]] 特征方差: [[0.25 0.25 0.25 0.25] [0.25 0.25 0.25 0.25]] 方差平滑: 4.25e-09 先验概率: [0.5 0.5] 预测标签: [[-67.6963115 -94.89631104]]




 冀公网安备13050302001966号
冀公网安备13050302001966号