转置卷积（Transposed Convolution），又叫反卷积（Deconvolution），是深度学习中用于进行反卷积操作的核心组件之一。它的作用是在卷积神经网络中对输入的特征图进行上采样的操作。与常规卷积操作不同，转置卷积用于将输入特征图的空间维度（如宽度和高度）扩展为更大的特征图。

简言之：转置卷积核作用是将低分辨率图像转换为高分辨率图像。

再次强调：转置卷积操作并不是真正的卷积的逆运算，因为信息的损失是不可逆的。逆卷积核的权重在训练过程中需要学习，类似于正常卷积操作中的卷积核。

参考资料：

1. conv_arithmetic/README.md at master · vdumoulin/conv_arithmetic · GitHub
2. 1603.07285.pdf (arxiv.org)

1. 卷积核计算

在 PyTorch 中，我们可以使用以下 API 进行转置卷积计算：

nn.ConvTranspose2d(
        in_channels: int,
        out_channels: int,
        kernel_size: _size_2_t,
        stride: _size_2_t = 1,
        padding: _size_2_t = 0,
        bias: bool = True,
        dilation: _size_2_t = 1,
        padding_mode: str = 'zeros',
)

参数含义如下：

1. in_channels 表示输入图像的通道数
2. out_channels 表示输出图像的通道数
3. kernel_size 表示每个通道卷积核大小
4. stride 表示每个像素点之间填充多少 (stride-1) 个 0
5. padding 表示在特征图周围填充 (kernel-padding-1) 行或列
6. bias 表示卷积核的偏置参数是否需要
7. padding_mode 在输入数据周围填充的数据，默认填充0

转置卷积计算的过程如下：

1. 首先，在输入图像每个像素之间填充 (stride-1) 行或列 0
2. 其次，在输入图像边缘填充 (kernel-padding-1) 行或列 0
3. 然后，将卷积核参数由上至下，从左向右翻转
4. 最后，在填充和翻转卷积核之后，使用翻转后的卷积核对填充后的图像进行卷积计算。

注意: 进行转置卷积操作时，padding 和 stride 只参与对输入图像的填充处理，后续只需要对处理后的图像进行正常的步长为 1 的卷积操作。

import torch
import torch.nn as nn
import torch.nn.functional as F


def test01():

    s = 2
    p = 1
    k = 3

    # 固定随机数
    torch.manual_seed(0)
    # 输入数据
    inputs = torch.randint(1, 10, size=(1, 1, 3, 3), dtype=torch.float32)
    # 卷积核参数: (每个卷积核的通道数，输出通道数量，卷积核宽高)
    weight = torch.randint(1, 5, size=(1, 1, 3, 3), dtype=torch.float32)
    # 偏置形状要和输出通道数一样
    bias = torch.zeros(size=(1,), dtype=torch.float32)

    outputs = F.conv_transpose2d(inputs, weight, bias, padding=p, stride=s)
    print('输出结果:\n', outputs)


# 分解动作
def test02():

    s = 2
    p = 1
    k = 3

    # 固定随机数
    torch.manual_seed(0)
    # 输入数据
    inputs = torch.randint(1, 10, size=(1, 1, 3, 3), dtype=torch.float32)
    weight = torch.randint(1, 5, size=(1, 1, k, k), dtype=torch.float32)

    # 1. 元素之间填充0
    new_inputs = torch.zeros(1, 1, 5, 5)
    new_inputs[:, :, ::s, ::s] = inputs
    print('元素填充:\n', new_inputs)

    # 2. 矩阵周围填充0
    inputs = F.pad(new_inputs, (k - p - 1,) * 4, value=0.0)
    print('周围填充:\n', inputs)

    # 3. 卷积核参数向下左右翻转
    weight = torch.flip(weight, dims=[2, 3])
    print('参数翻转:\n', weight)

    # 4. 正常进行卷积操作
    outputs = F.conv2d(inputs, weight=weight, padding=0, stride=1)
    print('输出结果:\n', outputs)


if __name__ == '__main__':
    test01()
    print('-' * 50)
    test02()

输出结果:
 tensor([[[[36., 28.,  4.,  6., 12.],
          [23., 63., 17., 56., 17.],
          [28., 29., 32., 31., 28.],
          [23., 47., 12., 29., 11.],
          [32., 26.,  8.,  8.,  8.]]]])
--------------------------------------------------
元素填充:
 tensor([[[[9., 0., 1., 0., 3.],
          [0., 0., 0., 0., 0.],
          [7., 0., 8., 0., 7.],
          [0., 0., 0., 0., 0.],
          [8., 0., 2., 0., 2.]]]])
周围填充:
 tensor([[[[0., 0., 0., 0., 0., 0., 0.],
          [0., 9., 0., 1., 0., 3., 0.],
          [0., 0., 0., 0., 0., 0., 0.],
          [0., 7., 0., 8., 0., 7., 0.],
          [0., 0., 0., 0., 0., 0., 0.],
          [0., 8., 0., 2., 0., 2., 0.],
          [0., 0., 0., 0., 0., 0., 0.]]]])
参数翻转:
 tensor([[[[1., 1., 1.],
          [3., 4., 1.],
          [3., 2., 4.]]]])
输出结果:
 tensor([[[[36., 28.,  4.,  6., 12.],
          [23., 63., 17., 56., 17.],
          [28., 29., 32., 31., 28.],
          [23., 47., 12., 29., 11.],
          [32., 26.,  8.,  8.,  8.]]]])

2. 特征图大小

转置卷积后的特征图形状的计算通常基于以下几个参数：

• \( H_{in} x W_{in} \) 表示输入特征图的形状
• \( K_{h} x K_{w} \) 表示卷积核的大小
• \( S \) 表示 stride 大小
• \( P \) 表示输入图形周围填充的 0

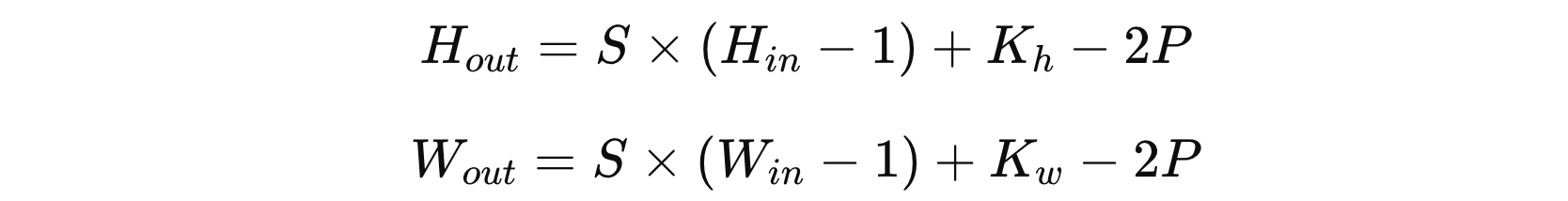
import torch.nn as nn
import torch


def demo():
    transpose_conv = nn.ConvTranspose2d(3, 6, kernel_size=3, stride=2, padding=2, bias=False)
    intputs = torch.randn(1, 3, 32, 32)

    # H_in = 32 W_in = 64
    # stride = 2
    # kenerl_size = 3
    # padding = 2
    # H_out = stride * (H_in - 1) + kenerl_size - 2 * padding
    # H_out = 2 * (32 - 1) + 3 - 2 * 2 = 61
    outputs = transpose_conv(intputs)
    print(outputs.shape)


if __name__ == '__main__':
    demo()

torch.Size([1, 6, 61, 61])

卷积核（Convolution Kernel）