GBDT 应用二分类问题

对于分类问题，GBDT 回归和分类一样，都可以使用不同的损失函数。对于二分类问题，最常用的是对数似然损失函数，损失函数公式如下：

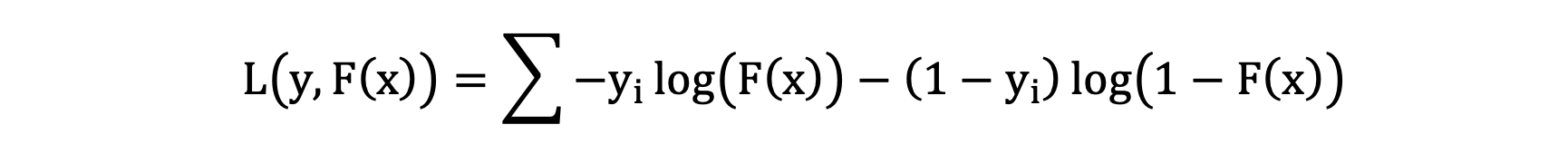
1. \(y_{i}\) 表示样本的真实类别（1表示正例、0表示负例）
2. F(x) 表示强学习器对样本的预测值
3. 损失值越小，说明模型对训练样本预测为正确类别的概率就越大

下面的公式的推导过程，主要计算当前这棵树拟合的目标值什么，以及当前这棵树叶子结点的最优输出值是什么。有了这两个，我们就可以构建决策树，以及计算叶子结点输出值了。

接着上面你的公式，因为 f(x) 是由多个弱学习器组合而成的强学习器，F(x) 可以用下面的公式表示：

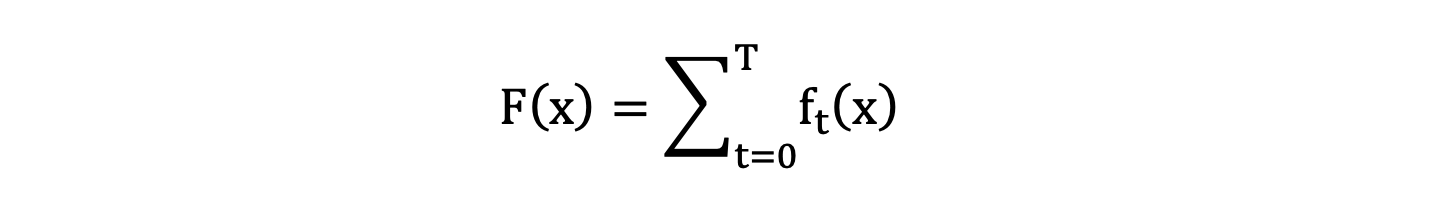
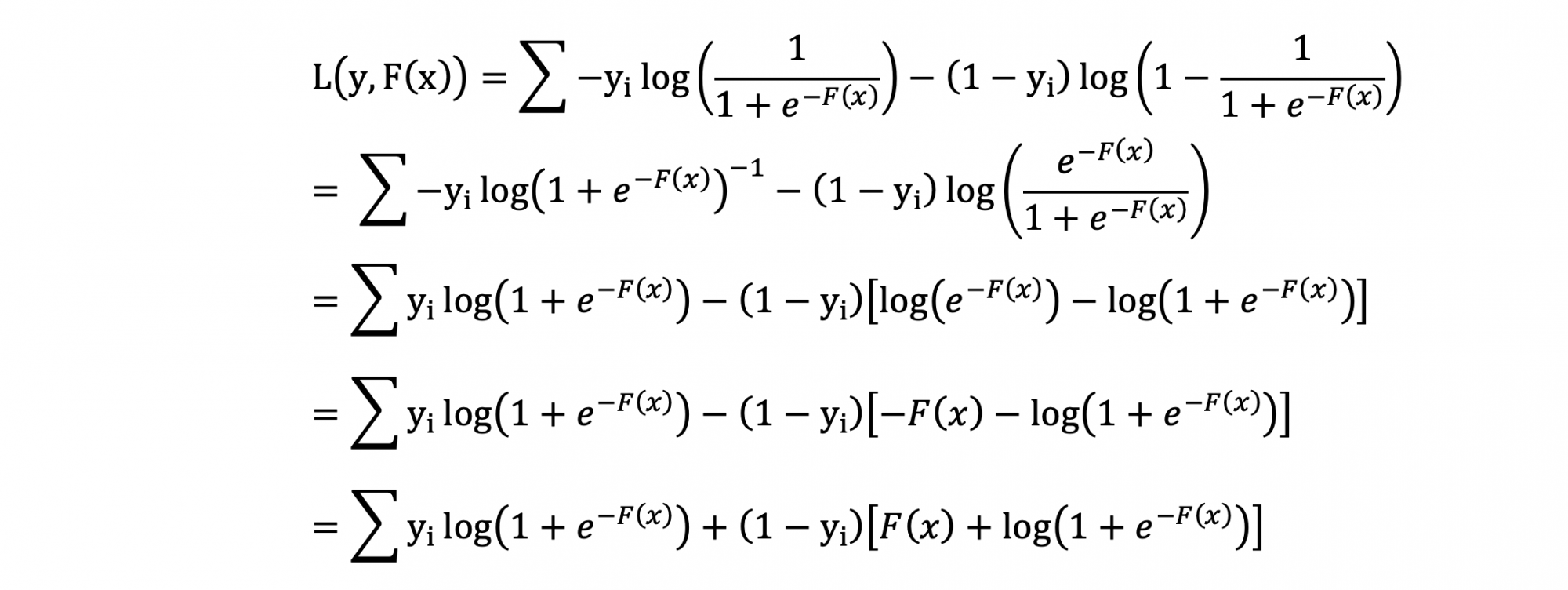
上面公司表示所有样本的总损失，每一个样本的损失值表示如下：

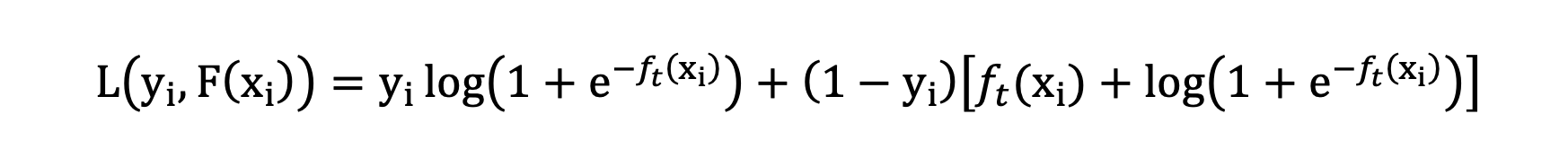
对 f_t 求导，计算当 f_t 输出什么值时，即: 当前这棵树拟合什么值时，当前树的损失最小。

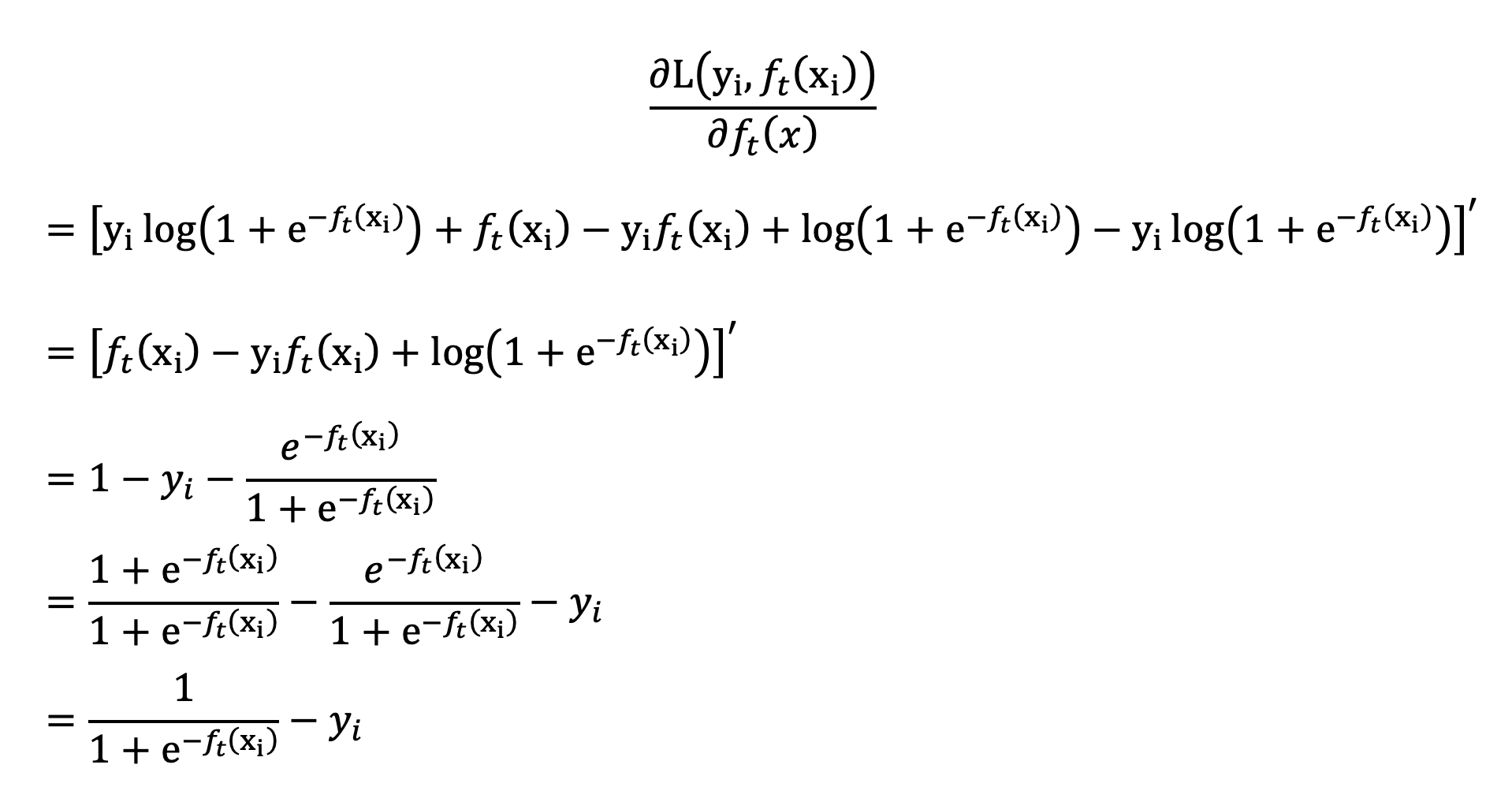
通过上面公式，我们知道上一棵树的梯度值，当前树要拟合的样本的负梯度为：

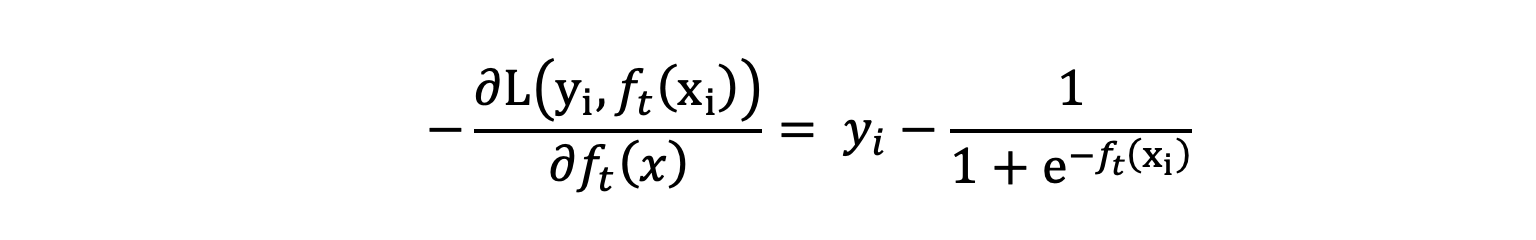
由于当前这棵树还没有构建完毕，我们还不能确定当前这棵树 f_t 最优输出值是什么，不过，我们可以使用泰勒二阶展开，使用上一棵树的输出值近似表示当前这棵树的近似最优输出值。接下来，需要求解上一棵树的一阶导、二阶导，从而构建出泰勒二阶展开公式，并对 f_t 求导，计算 f_t 的近似最优输出值。

一阶导上面的公式已经计算出来了，我们根据一阶导数再计算出二阶导数即可，如下所示：

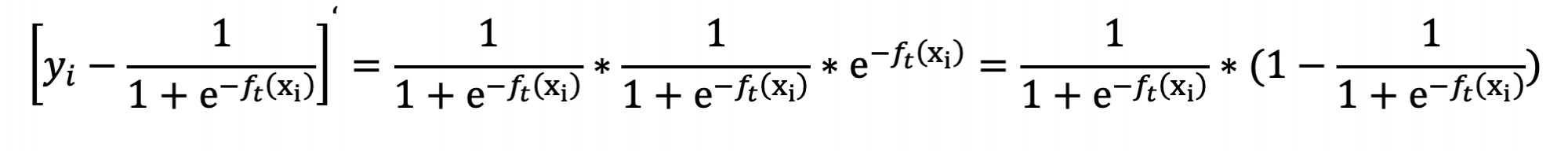
泰勒二阶展开公式如下：

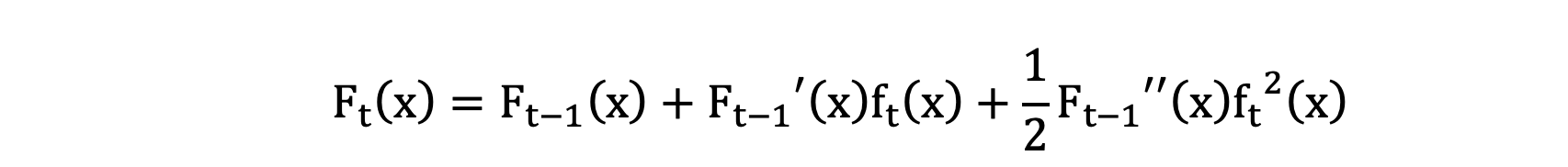
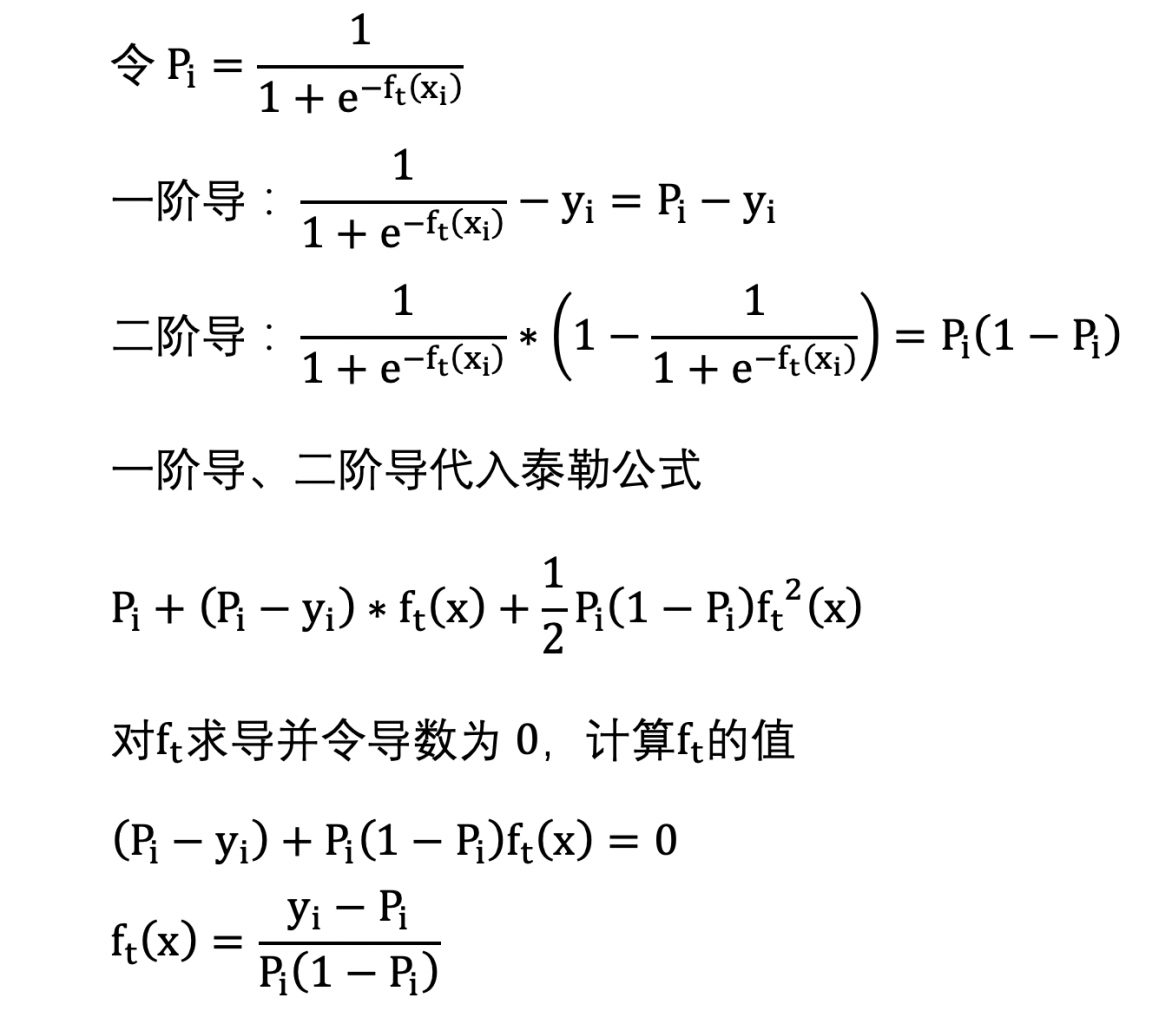
公式最后的这个式子即为：构建当前树时，叶子结点的最优输出值。构建 GBDT二分类树的过程如下：

1. 首先，初始化一个只包含一个结点的树桩
2. 然后，不停的去拟合负梯度，构建出指定个数的树
3. 叶子结点的最优输出值使用上面的公式计算即可