特征缩放（Feature Scaling）是机器学习中对特征进行归一化或标准化处理的技术，主要作用体现在多个方面。首先，它可以提高梯度下降的收敛速度。在梯度下降优化过程中，如果不同特征的取值范围相差较大，某些特征的梯度变化会远大于其他特征，使得优化过程变得缓慢甚至难以收敛。特征缩放能够让所有特征的数值范围相近，从而使梯度下降更加稳定，收敛速度更快。

其次，特征缩放可以避免特征权重的不均衡。在某些模型（如线性回归、逻辑回归、支持向量机）中，如果一个特征的取值范围远大于其他特征，模型可能会赋予其更大的权重，从而影响整体学习效果。通过特征缩放，可以确保所有特征的影响更加均衡，提高模型的表现。

此外，特征缩放还能提升基于距离的模型的效果，如 K 近邻（KNN）、K 均值聚类（K-Means）和支持向量机（SVM）。这些模型通常依赖欧几里得距离等度量方法，如果某个特征的数值远大于其他特征，它可能主导距离计算，使得模型过度关注该特征。特征缩放可以使所有特征在距离计算时贡献均衡，避免模型产生偏差。

最后，特征缩放对于主成分分析（PCA）也至关重要。PCA 通过计算协方差矩阵并提取主成分方向，如果特征的数值尺度不同，较大数值的特征可能主导方差分布，使得 PCA 难以正确提取主要信息。通过特征缩放，可以确保所有特征在相同尺度上，从而更准确地进行数据降维。

简言之，特征缩放在梯度下降、特征权重均衡、距离度量以及降维等方面都起到了关键作用，在许多机器学习模型中都是必要的预处理步骤。

1. Min-Max Scaling

Min-Max Scaling 是一种特征缩放方法，用于将数据线性变换到特定范围（通常是 [0, 1] 或 [−1, 1]）。该方法通过保持数据的相对关系来缩放数据，使其适用于需要归一化的机器学习和深度学习模型。

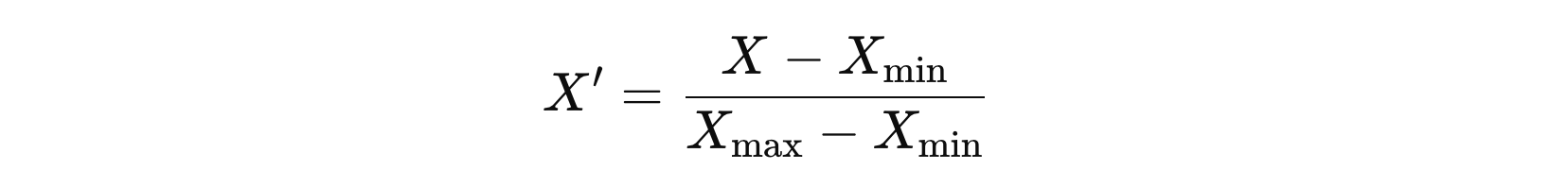
如果希望将数据缩放到 [a, b] 的区间，可以使用以下公式：

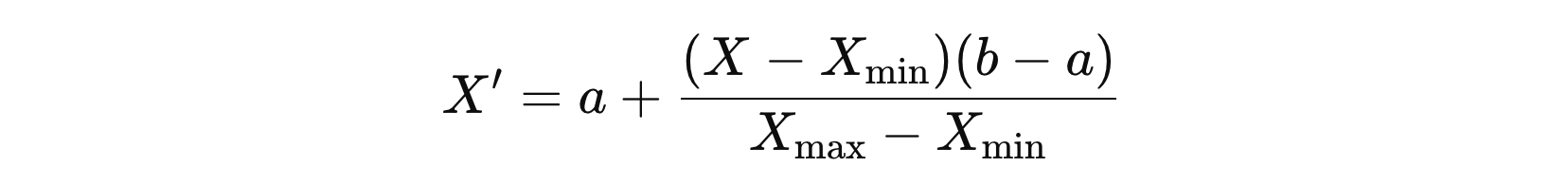
它可以保持原始数据的分布特性，不会改变数据的分布形状，而只是进行线性缩放。其次，该方法易于解释，因为所有特征值被缩放到相同的范围，便于可视化和理解。此外，在深度学习中，许多神经网络算法对输入数据的范围较为敏感，将数据归一化到 [0,1][0,1][0,1] 可以提高训练的稳定性和收敛速度。

然而，最小-最大缩放也存在一些缺点。它对异常值较为敏感，如果数据中存在极端值，最小值和最大值 可能会受到影响，从而导致大部分数据点被压缩到较小的范围。此外，该方法在数据分布未知或数据分布不均匀的情况下可能效果较差，无法有效调整数据的偏差。

from sklearn.preprocessing import MinMaxScaler
import numpy as np


def demo():
    data = np.random.rand(3, 5)
    print(data)
    print('-' * 58)
    scaler = MinMaxScaler(feature_range=(0, 1))
    data = scaler.fit_transform(data)
    print(data)


if __name__ == '__main__':
    demo()

[[0.14666549 0.43339182 0.52897234 0.07738186 0.03322054]
 [0.62278875 0.76554237 0.84991516 0.77921268 0.90327985]
 [0.31980854 0.59267591 0.92516213 0.00100069 0.36673218]]
----------------------------------------------------------
[[0.         0.         0.         0.09814957 0.        ]
 [1.         1.         0.81007342 1.         1.        ]
 [0.36365173 0.4795539  1.         0.         0.38332058]]

2. Standardization

标准化常用于数据预处理，特别是在机器学习建模前对特征进行归一化处理，使其均值为 0，标准差为 1。

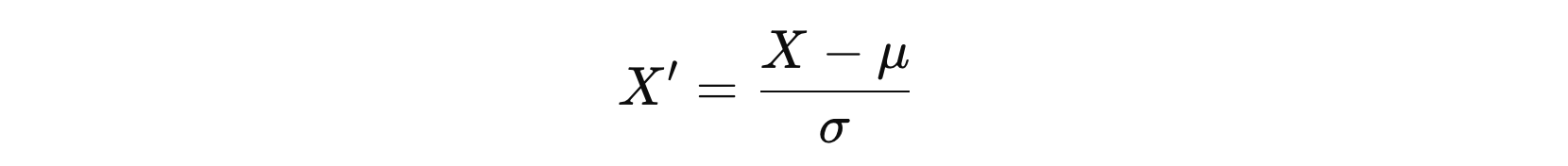
StandardScaler 主要适用于特征符合正态分布（Gaussian Distribution）的情况，因为它通过将数据转换为均值为0、标准差为1的标准正态分布来进行处理。这种标准化方式对于数据的分布特性要求较高，尤其是在特征本身呈现近似正态分布时效果最佳。

此外，StandardScaler 也广泛应用于梯度下降优化的算法，如线性回归、逻辑回归、支持向量机（SVM）和神经网络等。对于这些算法，特征的尺度差异可能会影响优化过程的效率和准确性。通过标准化，特征的尺度被统一，有助于加速模型的收敛，避免某些特征主导模型训练过程。

最后，StandardScaler 对于PCA（主成分分析）等依赖特征方差的算法也非常重要。PCA通过计算协方差矩阵来识别数据中最重要的方向，特征的方差大小会影响这些方向的计算。如果不进行标准化，方差较大的特征可能会主导PCA的结果，导致信息丢失或不准确的降维结果。因此，标准化能确保每个特征在计算过程中具有相等的权重。

from sklearn.preprocessing import StandardScaler
import numpy as np


def demo():
    data = np.random.rand(3, 5)
    print(data)
    print('-' * 58)
    scaler = StandardScaler(with_mean=True, with_std=True)
    data = scaler.fit_transform(data)
    print(data)


if __name__ == '__main__':
    demo()

[[0.83747337 0.97845394 0.40949502 0.54627312 0.69030563]
 [0.45168724 0.72848273 0.57987668 0.7775957  0.08334259]
 [0.48084205 0.7106001  0.29425162 0.53671803 0.20060058]]
----------------------------------------------------------
[[ 1.41095349  1.41169043 -0.15665    -0.66377378  1.39056845]
 [-0.78858918 -0.63271797  1.29553311  1.41334576 -0.91830785]
 [-0.62236431 -0.77897247 -1.13888311 -0.74957197 -0.4722606 ]]