在训练深度模型（如 RNN、Transformer）时，由于网络层数较深，随着训练进行，网络各层的输入分布不断变化，这会导致训练变慢，甚至无法收敛。为了解决这个问题，层归一化（LN）应运而生。它通过标准化每一层的输出，减少层间输入分布的差异，从而加速训练并提高收敛性。

需要注意的是，批量归一化（BN）在处理数据时，会计算整个批次的均值和方差来标准化每个特征，而层归一化则在每个样本内独立计算该样本的均值和方差，对该样本的所有特征进行标准化。假设我们有以下两个样本组成一个批次：

样本	特征1	特征2	特征3
样本1	1.0	2.0	3.0
样本2	4.0	5.0	6.0

• 批量归一化会在整个批次上计算每个特征的均值和方差，然后用这些值来标准化每个特征。
• 层归一化则会在每个样本内独立计算均值和方差，标准化每个样本的所有特征。

1. LN 计算公式

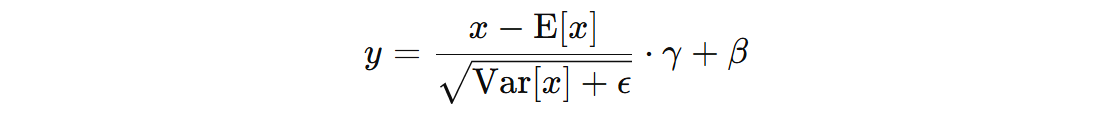
1. \( x \) 表示输入数据
2. \( E[x] \) 表示 token 或者 sentence 的均值
3. \( Var(x) \) 表示 token 或者 sentence 的方差
4. \( \epsilon \) 是一个小常数 1e-5，用于避免除以零的情况
5. \( \gamma \) 是学习参数，用来控制标准化后的数据的尺度。该参数会通过反向传播进行更新
6. \( \beta \) 是学习参数，用来控制标准化后的数据的平移（数据的均值调整）。该参数也会通过反向传播进行更新

经过 LN 后每个 Token 的分布调整为均值为 0，方差为 1，然后再通过 γ、β 参数对数据分布进行调整，使得网络能够根据数据的特性、适应不同的输入分布，从而进行更合适的学习，提高训练稳定性并加速收敛。

LN 和 BN 一样，通常用在激活函数之前。这是因为激活函数的作用是引入非线性，使得神经网络能够学习复杂的模式和函数。如果 LN 在激活函数之后执行，它会在已经非线性的输出上进行标准化，这可能破坏网络的表达能力和非线性特性，影响模型的学习能力。

注意：LN 可以灵活地进行归一化，并且可以选择以 sentence 或 token 为单位进行归一化，具体取决于任务需求和应用场景。另外，LN 不需要在训练时累计 BN 的 running_mean 和 running_var 值。

2. LN 使用示例

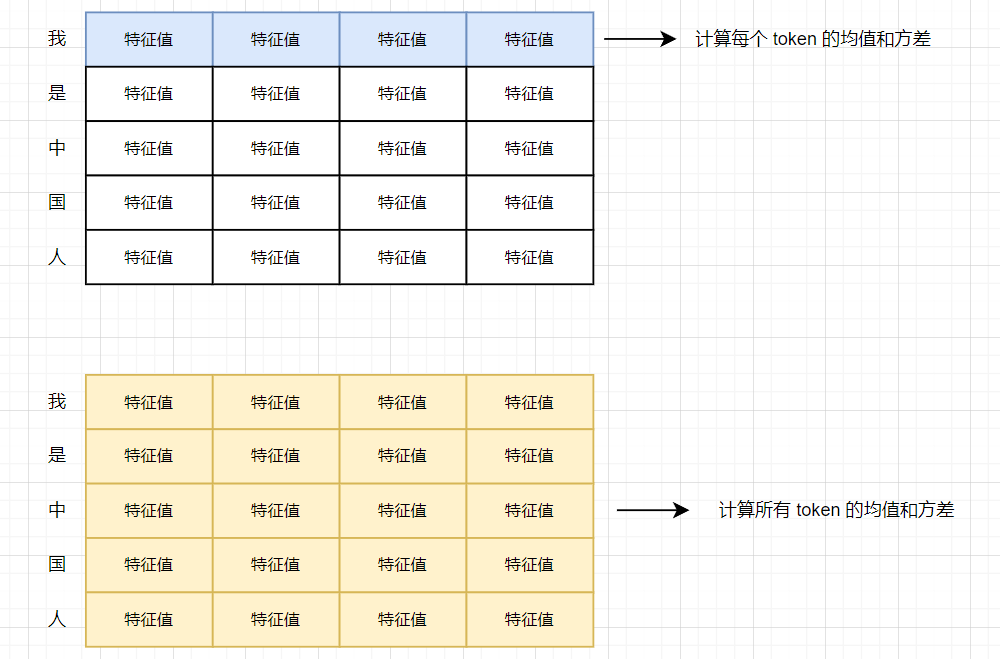
LN 如果以 token 为单位归一化，则需要计算每个 token 的均值和方差。如果以 sentence 为单位进行归一化，则将 sentence 中的所有值计算均值和方差。

import torch.nn as nn
import torch


torch.manual_seed(42)
batch, seq_len, dim = 2, 3, 4
batch_inputs = torch.rand(size=(batch, seq_len, dim))


def test01():
    # 以 Token 为单位
    layer_norm = nn.LayerNorm(normalized_shape=dim, eps=1e-5, elementwise_affine=False, bias=False)
    output = layer_norm(batch_inputs)
    print(output)

    # 以句子为单词
    layer_norm = nn.LayerNorm(normalized_shape=(seq_len, dim), eps=1e-5, elementwise_affine=False, bias=False)
    output = layer_norm(batch_inputs)
    print(output)


def test02():
    # 以 Token 为单位
    mean = torch.mean(batch_inputs, dim=2)
    var = torch.var(batch_inputs, dim=2, unbiased=False)
    print('均值:', mean, '方差:', var)
    outputs = (batch_inputs - mean.view(2, 3, 1)) / torch.sqrt(var.view(2, 3, 1) + 1e-5)
    print(outputs)

    # 以句子为单词
    mean = torch.mean(batch_inputs, dim=(1, 2))
    var = torch.var(batch_inputs, dim=(1, 2), unbiased=False)
    print('均值:', mean, '方差:', var)
    outputs = (batch_inputs - mean.view(2, 1, 1)) / torch.sqrt(var.view(2, 1, 1) + 1e-5)
    print(outputs)


if __name__ == '__main__':
    test01()
    print('-' * 50)
    test02()

程序执行结果：

tensor([[[ 0.4168,  0.5568, -1.7200,  0.7464],
         [-0.5865,  0.4426, -1.2412,  1.3851],
         [ 0.8792, -1.5672,  0.8605, -0.1725]],

        [[ 1.3004, -0.5034,  0.5333, -1.3303],
         [ 1.3505, -0.0656, -1.4626,  0.1778],
         [-0.8480, -0.0826, -0.7264,  1.6570]]])
tensor([[[ 0.8209,  0.9359, -0.9335,  1.0915],
         [-0.9069, -0.1676, -1.3772,  0.5096],
         [ 1.0264, -1.8107,  1.0047, -0.1933]],

        [[ 1.3728,  0.0045,  0.7909, -0.6228],
         [ 1.4455,  0.0326, -1.3612,  0.2754],
         [-1.3474, -0.5685, -1.2236,  1.2017]]])
--------------------------------------------------
均值: tensor([[0.7849, 0.5104, 0.6505],
        [0.6519, 0.5883, 0.4599]]) 方差: tensor([[0.0546, 0.0418, 0.1090],
        [0.0280, 0.0484, 0.0503]])
tensor([[[ 0.4168,  0.5568, -1.7200,  0.7464],
         [-0.5865,  0.4426, -1.2412,  1.3851],
         [ 0.8792, -1.5672,  0.8605, -0.1725]],

        [[ 1.3004, -0.5034,  0.5333, -1.3303],
         [ 1.3505, -0.0656, -1.4626,  0.1778],
         [-0.8480, -0.0826, -0.7264,  1.6570]]])
均值: tensor([0.6486, 0.5667]) 方差: tensor([0.0810, 0.0486])
tensor([[[ 0.8209,  0.9359, -0.9335,  1.0915],
         [-0.9069, -0.1676, -1.3772,  0.5096],
         [ 1.0264, -1.8107,  1.0047, -0.1933]],

        [[ 1.3728,  0.0045,  0.7909, -0.6228],
         [ 1.4455,  0.0326, -1.3612,  0.2754],
         [-1.3474, -0.5685, -1.2236,  1.2017]]])