在数据分析中，K-means 聚类是一种非常常用的聚类方法。它的核心思想是：将相似的数据点归为同一簇，并为每个簇计算一个质心，然后把每个点分配到距离最近的质心所属簇中。

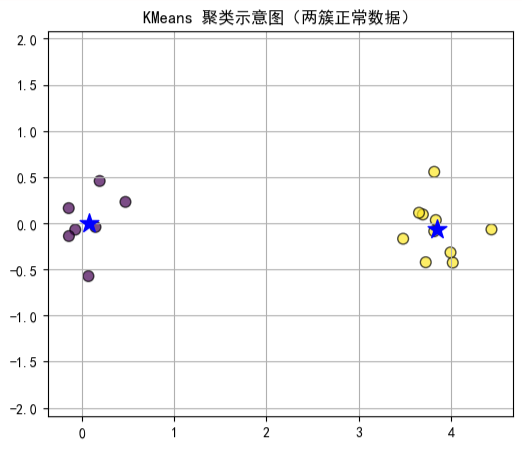
这种方法简单高效，但也存在一些明显的局限性：

对噪声和异常点敏感：极端值会影响质心的位置，从而扭曲聚类结果。
需要预先指定簇的数量：在实际场景中，簇的数量往往未知，而错误的预设可能导致聚类不准确。
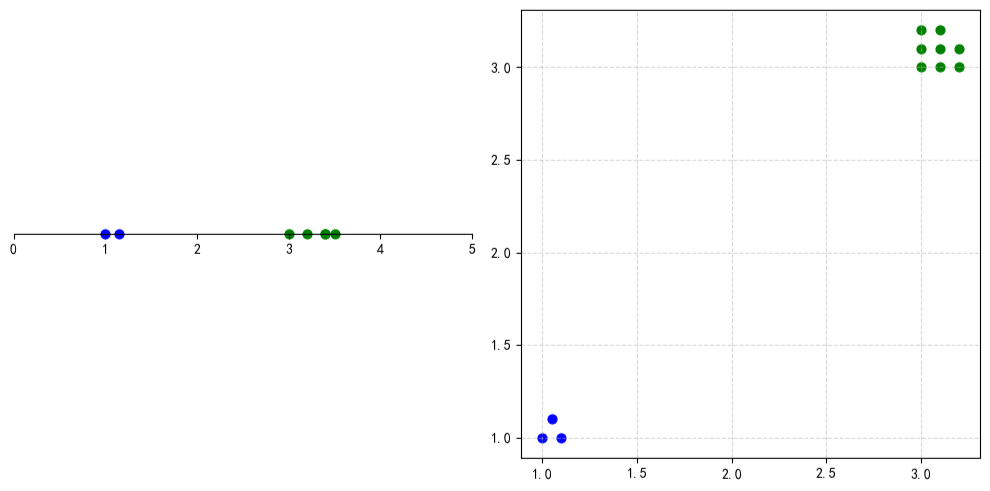
对复杂数据分布适应性差：对于非球形或不规则形状的簇，K-means 很难得到理想的划分。

如下图所示，我们可以看到 K-means 在某些复杂数据分布下的聚类效果并不理想。

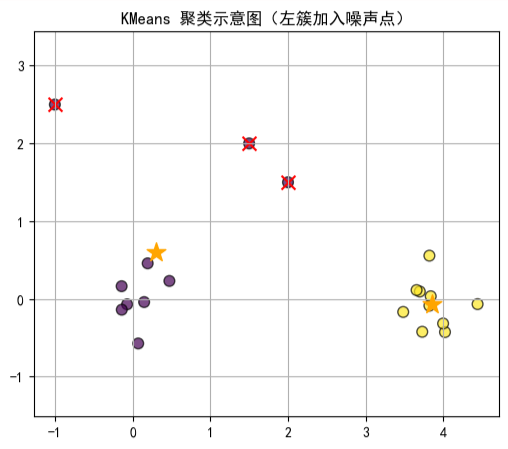
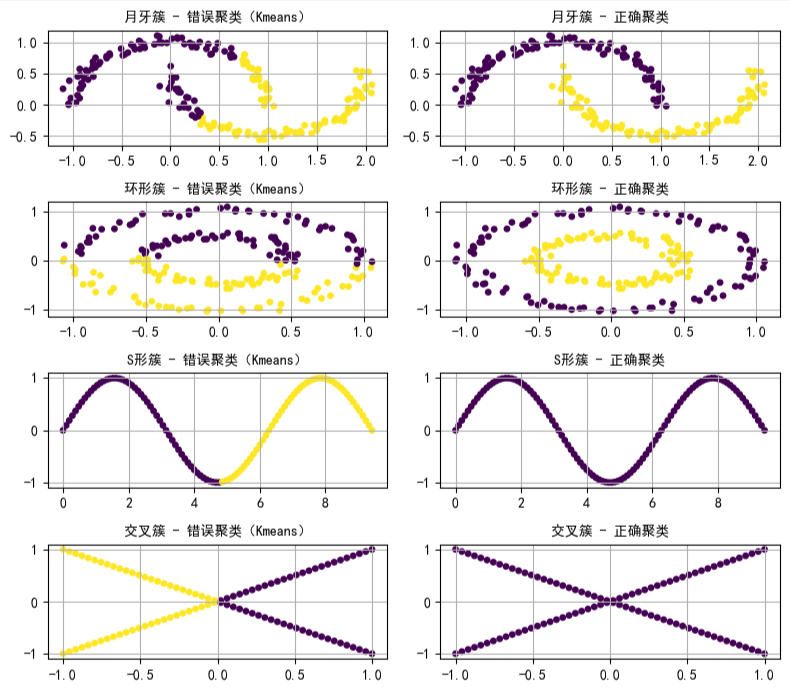
为了克服这些问题，DBSCAN（Density-Based Spatial Clustering of Applications with Noise）应运而生。它是一种基于密度的聚类方法，相比 K-means 有几个明显优势：

无需预先指定簇的数量，能够自动发现簇的数量。
能够识别任意形状的簇，不局限于球形。
自动识别噪声点，避免异常点干扰聚类结果。

这里的密度指的是单位区域内点的多少，简单来说，DBSCAN 就是找点多的地方，把它们聚成簇，把点少的地方当作噪声。

凭借这些特点，DBSCAN 在地理信息分析、图像处理、数据挖掘等领域得到了广泛应用。

其他链接：
基于质心的聚类方法：https://mengbaoliang.cn/archives/93699/
基于分布的聚类方法：https://mengbaoliang.cn/archives/tag/gshh/

1. 算法原理

在理解 DBSCAN 聚类原理之前，先要明确一点，在聚类的过程中，DBSCAN 会把所有数据点分成三类：

核心点：在半径 epsilon 范围内至少有 min_samples 个点（算上自己）
边界点：自己周围点数不够 min_samples，但落在某个核心点的 epsilon 范围内
噪声点：既不是核心点，也不在任何核心点的 epsilon 范围内

A	B	C	D	E	F	G	H	I	J
(1,1)	(1,2)	(2,1)	(2,2)	(0.5,2.5)	(8,8)	(8,9)	(9,8)	(7.5,9.5)	(5,5)

假设：epsilon = 1.5、min_samples = 3

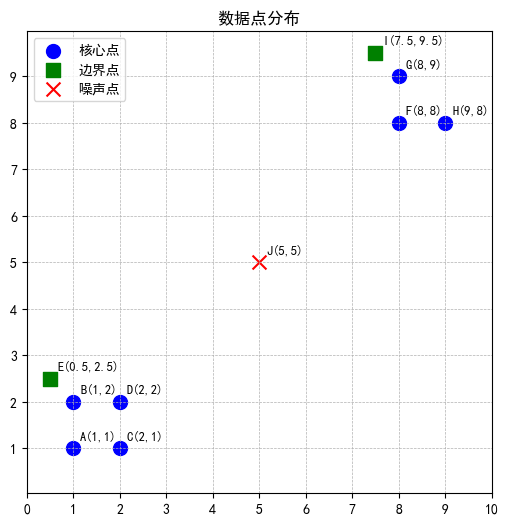
接下来，我们看看具体的聚类过程。计算每个数据点到其他数据点的距离：

	A	B	C	D	E	F	G	H	I	J
A	0.000	1.000	1.000	1.414	1.581	9.899	10.630	10.630	10.700	5.657
B	1.000	0.000	1.414	1.000	0.707	9.220	9.899	10.000	9.925	5.000
C	1.000	1.414	0.000	1.000	2.121	9.220	10.000	9.899	10.124	5.000
D	1.414	1.000	1.000	0.000	1.581	8.485	9.220	9.220	9.301	4.243
E	1.581	0.707	2.121	1.581	0.000	9.301	9.925	10.124	9.899	5.148
F	9.899	9.220	9.220	8.485	9.301	0.000	1.000	1.000	1.581	4.243
G	10.630	9.899	10.000	9.220	9.925	1.000	0.000	1.414	0.707	5.000
H	10.630	10.000	9.899	9.220	10.124	1.000	1.414	0.000	2.121	5.000
I	10.700	9.925	10.124	9.301	9.899	1.581	0.707	2.121	0.000	5.148
J	5.657	5.000	5.000	4.243	5.148	4.243	5.000	5.000	5.148	0.000

统计每个数据点的邻域

数据点	邻域点集合	邻域点数量	数据点类型
A(1,1)	A, B, C, D	4	核心点
B(1,2)	A, B, C, D, E	5	核心点
C(2,1)	A, B, C, D	4	核心点
D(2,2)	A, B, C, D	4	核心点
E(0.5,2.5)	B, E	2	边界点
F(8,8)	F, G, H	3	核心点
G(8,9)	F, G, H, I	4	核心点
H(9,8)	F, G, H	3	核心点
I(7.5,9.5)	G, I	2	边界点
J(5,5)	J	1	噪声点

开始聚类：

第一步：外层循环遍历数据点

访问 A：A 未访问且为核心点 → 创建簇 C1
将 A 的邻域 {A, B, C, D} 全部加入簇
核心邻居 B、C、D 入队列等待扩展 → 队列状态 [B, C, D]

第二步：内层队列扩展簇 C1

出队 B：邻域 {B, E, A, D, C}
- E 不是核心点，但在 B 的邻域内 → 加入簇作为边界点，不入队
- 队列更新为 [C, D]
出队 C：邻域 {C, A, D, B} 已全部在簇中 → 无新增，队列 [D]
出队 D：邻域 {D, B, C, A} 已全部在簇中 → 队列清空，C1 扩展完成

第三步：外层循环继续遍历

遇到 B、C、D、E 已访问 → 跳过
下一个未访问核心点 F → 创建簇 C2
将 F 的邻域 {F, G, H} 加入簇
核心邻居 G、H 入队列 → 队列状态 [G, H]

第四步：内层队列扩展簇 C2

出队 G：邻域 {G, I, F, H}
- I 不是核心点，但在 G 的邻域内 → 加入簇作为边界点，不入队
- 队列更新为 [H]
出队 H：邻域 {H, F, G} 已全部在簇中 → 队列清空，C2 扩展完成

第五步：外层循环继续遍历剩余数据点

I 已访问 → 跳过
J 未访问且邻域点数 < min_samples，且不在任何核心点邻域 → 判定为噪声点

第六步：最终聚类结果

簇 C1：核心点 A、B、C、D；边界点 E
簇 C2：核心点 F、G、H；边界点 I
噪声点：J

通过对 DBSCAN 聚类过程的了解，我们可以发现，簇的形成和扩展是依靠核心点推动的，而边界点会被吸收进簇，噪声点则不属于任何簇。

简单总结下，在 DBSCAN 里，簇是长出来的，而不是一开始就分好的。整个聚类的过程可以想成：

找到一个核心人物（邻居够多的点）。
这个核心人物会把自己周围（epsilon 范围内）的邻居都拉进来。
新进来的点如果自己也是“核心”，就继续往外扩 → 簇就这样不断生长。
如果一个点既不是核心，也没有核心愿意拉它，就成了噪声。

另外，我们也发现 DBSCAN 聚类过程中，寻找邻域需要大量的计算。例如：要对 1000 条数据进行聚类，则会进行 100 万次的距离计算，如果数据维度较高，则会需要更多的计算时间。所以，DBSCAN 的聚类优化，主要是通过对邻域计算的优化来提升聚类效率。常见的是，使用 KD TREE 或者 BALL TREE，KD Tree 适合低维数据（通常 20 维），BALL tree 适合较高维数据（20 维以上）。

2. 样本归簇

在很多聚类算法中，例如 K-Means 和高斯混合模型（GMM），训练结束后通常会提供 predict 接口。当新样本到来时，无需依赖原始数据的完整分布，只需基于模型训练得到的簇的数学描述，即可直接判定新样本的簇归属。例如：

K-Means：训练后会得到各簇的质心，新样本的归属可通过计算其与各质心的距离确定
高斯混合模型（GMM）：训练后会输出每个高斯子分布的均值、方差、混合系数，新样本的归属可通过计算其在各子分布下的概率密度，选择概率最大的簇作为结果

但 DBSCAN 与二者存在本质区别：DBSCAN 的核心逻辑是基于密度划分簇，它仅对已有训练数据点完成标记，例如：哪些点属于某一簇、哪些点是噪声点，并不会生成质心或者概率分布这类可描述簇形态的数学参数。

因此，DBSCAN 本质上是一种非参数化、完全依赖原始数据密度分布的聚类算法：由于缺乏对簇的通用数学描述，它无法像 K-Means 或 GMM 那样，直接通过 predict 接口判定新样本的簇归属（若要处理新样本，需将其重新放入原始数据集，结合密度规则重新计算）。

3. 设置参数

DBSCAN 聚类需要两个非常关键的超参数：epsilon（邻域半径） 和 min_samples（核心点的最少邻居数）。
这两个参数的选择会直接影响聚类效果。虽然没有一个固定的“最佳公式”，但有一些直观的经验方法可以帮助我们更合理地设置。

在实践中，通常建议 先确定 min_samples，再选择合适的 epsilon。

3.1 min_samples

min_samples 最常用的参考公式为：

min_samples ≈ 数据维度 + 1

这样设置的直观意义是：在 d 维空间中，核心点的邻域至少需要 d+1 个点，才能形成一个稳定的几何结构，从而保证簇的密度足够高。举几个例子：

1 维空间：1 维空间是直线，要形成密集段，一个点至少需要 1 个相邻点（加上自身共 2 个）
2 维空间：2 维空间是平面，要形成密集区域，至少需要 3 个点才能构成最小三角形单元
d 维空间：需要 d+1 个点才能支撑起 d 维空间的最小密集结构，避免因点数量过少导致误判密集区域

注意：这个公式并不是硬性规定，只是一种基于几何直觉的经验参考。实际中，还需要结合数据分布进行调整。

注意：这只是一个 “入门级参考标准”，并非绝对准则。实际应用中，若数据噪声较多，可适当增大 min_samples（如取 d+2、d+3），减少噪声点被误判为核心点的概率；若数据簇本身较稀疏，可适当减小 min_samples，避免漏判核心点。

3.2 epsilon

当 min_samples 确定后，epsilon 的作用就是划定邻域范围，确保核心点的邻域内，能稳定包含至少 min_samples 个样本。此时最有效的方法是K 距离图法，其中 “K 值” 需与已确定的 min_samples 保持一致，即 K=min_samples。

下面举个例子，假设有 5 个数据点，k = 3（min_samples = 3）

A(1,1), B(2,2), C(2,0), D(5,5), E(8,8)

计算每个点到其他点的距离：

点	A	B	C	D	E
A	0	1.41	1.41	5.66	9.90
B	1.41	0	2.00	4.24	8.49
C	1.41	2.00	0	5.83	10.00
D	5.66	4.24	5.83	0	4.24
E	9.90	8.49	10.00	4.24	0

对每个点，把距离排序，取第 3 个最近邻距离（k = 3）

点	升序距离（不含自己）	第 3 近邻距离
A	1.41, 1.41, 5.66, 9.90	5.66
B	1.41, 2.00, 4.24, 8.49	4.24
C	1.41, 2.00, 5.83, 10.00	5.83
D	4.24, 4.24, 5.66, 5.83	5.66
E	4.24, 8.49, 9.90, 10.00	9.90

排序第 3 近邻距离：4.24、5.66、5.66、5.83、9.90，并绘制 K 距离图：

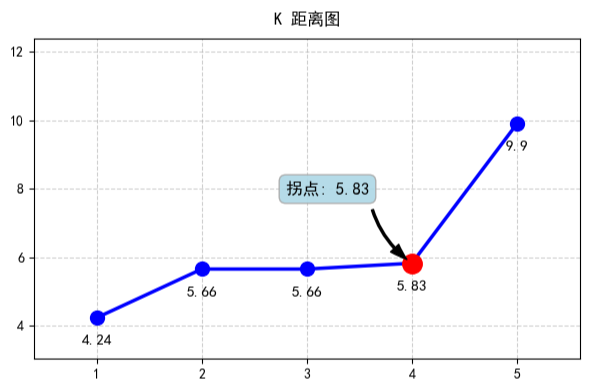
在上图中：

K 距离较小的点，说明它周围邻居密集
K 距离较大的点，说明点周围邻居稀疏
密集区域和稀疏区域之间的点称作拐点

拐点左侧是高密度区域，右侧是低密度区域，因此 epsilon 应取拐点附近的区间，避免将低密度样本误判为核心点。上图这种情况，我们可以大概在 [5.66, 5.83] 之间选择一个作为 epsilon 的值，这样能让 DBSCAN 准确识别核心点和噪声点，得到合理的聚类结果。

注意：即使初步选择的 epsilon 值参考了 K 距离图，聚类效果可能仍存在不足，此时可以通过微调 epsilon 和 min_samples，以获得更合理的簇划分。

4. 接口使用

import numpy as np
from sklearn.cluster import DBSCAN
import pandas as pd


def demo():
    points = np.array([[1, 1], [1, 2], [2, 1], [2, 2], [0.5, 2.5], [8, 8], [8, 9], [9, 8], [7.5, 9.5], [5, 5]])
    columns = ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J']

    # algorithm 邻域搜索算法，可选值：auto、ball_tree、kd_tree、brute
    # metric 样本距离计算方法，例如：euclidean、cosine、minkowski、manhattan
    dbscan = DBSCAN(eps=1.5, min_samples=3, metric='euclidean', algorithm='brute')
    result = dbscan.fit_predict(points)

    # 聚类结果
    # [ 0  0  0  0  0  1  1  1  1 -1]
    # 0 表示第一个簇
    # 1 表示第二个簇
    # -1 表示噪声点
    print(result)

    # 核心样本索引：[0 1 2 3 5 6 7]
    print(dbscan.core_sample_indices_)
    # 具体核心样本：[[1. 1.] [1. 2.] [2. 1.] [2. 2.] [8. 8.] [8. 9.] [9. 8.]]
    print(dbscan.components_)


if __name__ == '__main__':
    demo()

基于密度的聚类方法（DBSCAN）