线性判别分析（Linear Discriminant Analysis，简称 LDA）是一种经典的统计学方法，主要用于 特征降维 和 分类问题。

它的核心思想是：寻找一个最佳的线性投影，使得投影后的数据在新空间中，不同类别之间的间隔最大化，而同一类别的数据尽可能聚集，从而提高分类效果。

1. 判别函数

线性判别分析通过假设数据符合高斯分布，来估计一个样本属于某个类别的后验概率。

• 首先，计算一个样本属于每个类别的先验概率（粗略估计）
• 然后，计算一个样本从不同类别中产生的可能性（数据分布）
• 最后，结合两者得到一个样本属于某个类别的后验概率

对于一个新样本，后验概率计算如下（第二项表示先验概率）：

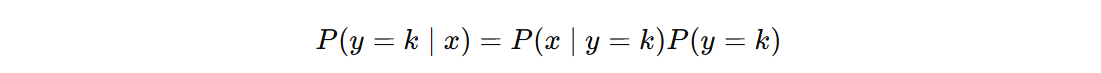
假设各类别的数据服从多元高斯分布：

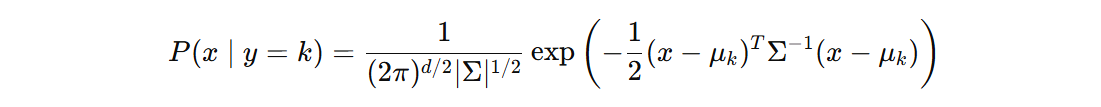
将 \( P(x \mid y = k) \) 的高斯分布形式代入后：

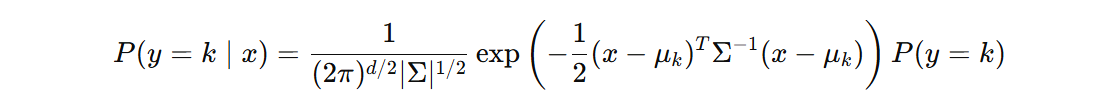
取对数简化：

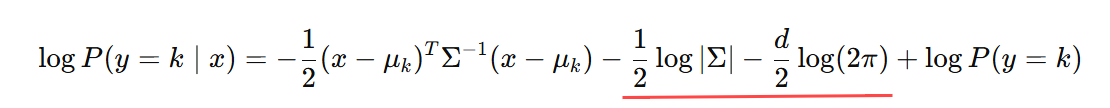
公式中一共有四项，对于分类问题第二项（假设：所有类别数据协方差矩阵相同）、第三项（常数）对于所有类别都是一样的，可以去掉，并将第一项展开：

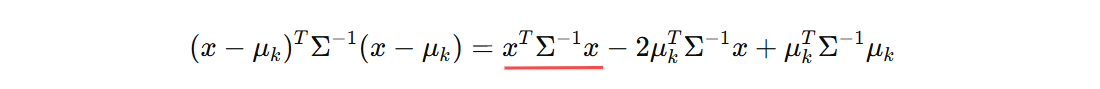
再次去掉对分类无关的项（对于分类，第一项对于所有类别计算结果都相同），得到如下：

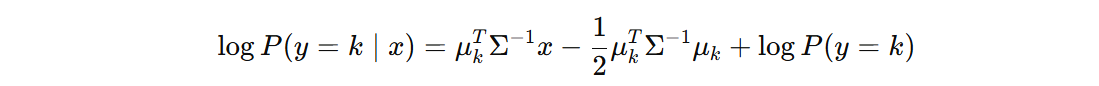
我们得到 w 和 b 的计算公式：

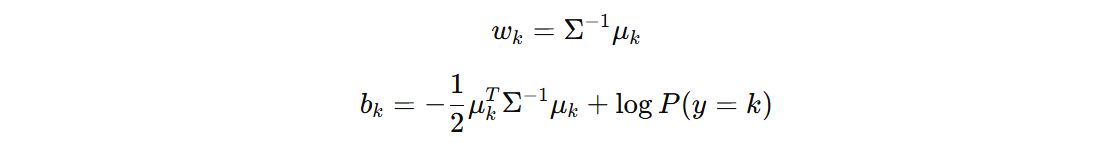
线性判别分析用于分类的判别函数可以表示如下：

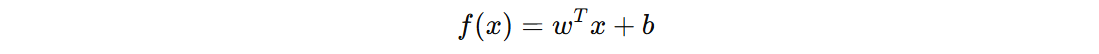
最后，我们使用线性判别函数 \(f(x)\) 来将样本归类到判别分数最大的类别。

2. 核心思想

线性判别分析算法是一个线性分类器。对于线性可分的数据（即数据可以通过一条直线或一个超平面完全分开）分类性能非常好。所以，我们思考下，对于下面这两种分布的数据，哪种能够获得更好的分类器？

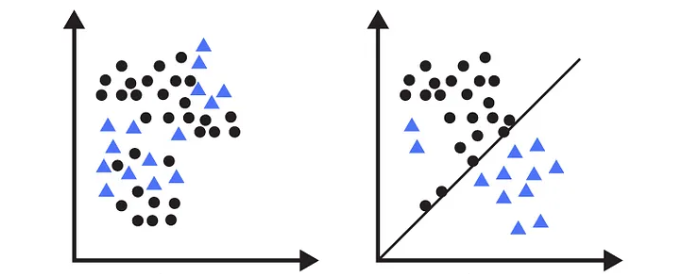
显然，第二种分布的数据训练得到的分类器性能更好。即：为了提高分类器的性能，我们得去优化原始数据的分布。这种优化我们可以通过将数据投影、变换到新的空间来实现。新的空间应该满足什么条件？

在原始数据空间中，数据的分布可能具有以下问题：

• 类间距离不足： 不同类别的均值距离很近，难以分辨。
• 类内分散过大： 同类样本点分布较广，造成边界模糊。

LDA 希望把原始数据投影到一个新的空间（改变数据的分布），这个空间满足：类间距离足够大，类内更加集中。在这个空间中，更容易、更准确的计算分类的判别分数。

为了找到这个满足这个条件的空间，我们接下来，需要进行一些数学公式的推导。

类内的散度矩阵：

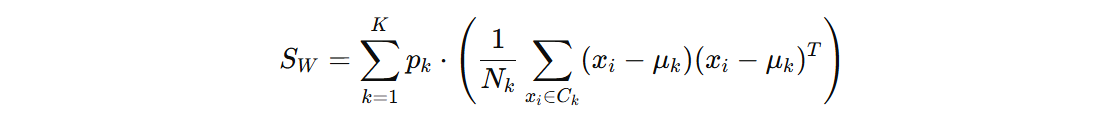
• \(p_{k}\) 表示第 k 类的权重
• \(X_{k}\) 第 k 类的样本集合
• \(x_{i}\) 第 k 类别中的样本
• \(μ_{k}\)​​ 是第 k 类的均值向量

类间的散度矩阵：

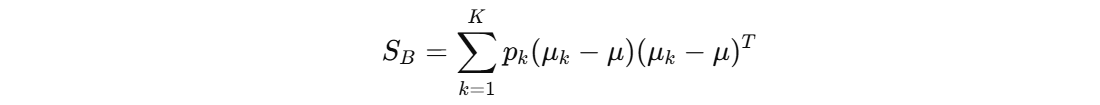
• \(p_{k}\)​ 表示第 k 类的权重
• \(μ_{k}\)​ 是第 k 类的均值向量
• \(μ\) 是所有样本的均值向量

目标：找到一个新空间 W，使得类间散布（分子部分）最大化，同时类内散布（分母部分）最小化。

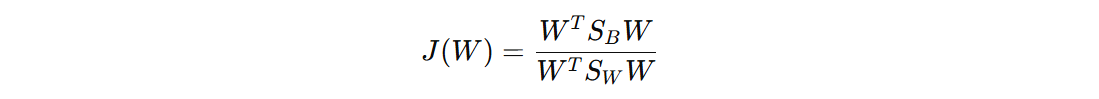
• \(S_{B}\)​ 是类间散度矩阵，描述了不同类别之间的离散程度
• \(S_{W}\)​ ​ 是类内散度矩阵，描述了同一类别内部的离散程度
• \(W\)​ 是投影矩阵，它表示新空间的投影方向

接下来，通过优化的方式进行推导，目标函数的最大化问题可以转化为广义特征值问题的求解。

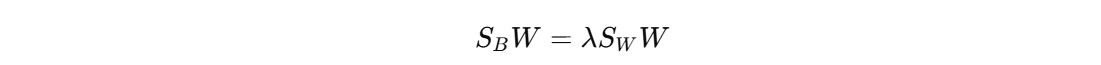
其中 λ 是特征值，对应的 W 是特征向量，即：投影矩阵。接下来，我们将数据投影到新的空间中，再计算样本属于每个类别的分数。

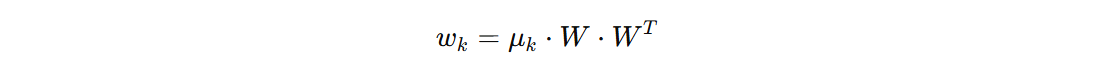
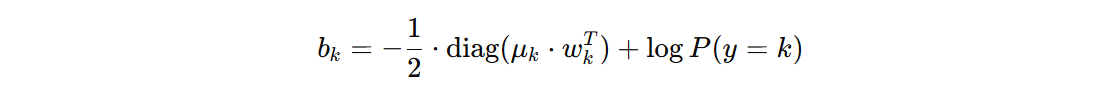
公式中，出现两个 W 的计算，其中一个 W 用于将输入的数据投影到新的空间。偏置项计算完成之后是一个 (n_classes, n_classes) 形状，我们使用 diag 取对角线的值。

3. 计算过程

通过前面的学习，我们已经了解线性判别分析算法的分类原理，接下来，我们通过代码来展示其具体的计算过程，从而加深对算法原理的理解。

3.1 分类计算

import numpy as np
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from scipy import linalg


X, y = make_classification(n_samples=1000, n_features=5, n_informative=5, n_redundant=0, n_classes=3, random_state=42)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)


def test01():
    estimator = LinearDiscriminantAnalysis(solver='eigen')
    estimator.fit(X_train, y_train)
    print('Acc: %.3f' % estimator.score(X_test, y_test))


def test02():
    # 类别均值
    class_means = np.zeros((3, 5))
    for i in range(3):
        class_means[i, :] = np.mean(X_train[y_train == i], axis=0)

    # 计算每个类别的先验概率
    counts = np.array([sum(y_train == label) for label in [0, 1, 2]])
    priors = counts / len(y_train)

    # 类内散度
    sw = np.zeros(shape=(X_train.shape[1], X_train.shape[1]))
    for label in range(3):
        xc = X_train[y_train == label, :]
        xw = np.zeros(shape=(X_train.shape[1], X_train.shape[1]))
        for x in xc:
            x_centered = x - class_means[label]
            x_centered = x_centered[:, None]
            xw += (x_centered @ x_centered.T)

        xw /= xc.shape[0]
        xw *= priors[label]
        sw += xw

    # 计算类间散度
    sb = np.zeros(shape=(X_train.shape[1], X_train.shape[1]))
    total_mean = np.mean(X_train, axis=0)
    for label in range(3):
        xb_centered = class_means[label, :] - total_mean
        xb_centered = xb_centered[:, None]
        sb += priors[label] * xb_centered @ xb_centered.T

    # 计算投影空间
    eigen_value, eigen_vector = linalg.eigh(sb, sw)
    eigen_vector = eigen_vector[:, np.argsort(eigen_value)[::-1]]

    # 计算决策函数参数
    w = np.dot(class_means, eigen_vector)
    b = -0.5 * np.diag(np.dot(class_means, eigen_vector) @ np.dot(class_means, eigen_vector).T) + np.log(priors)

    # 测试集评估
    y_correct = 0
    for x, y_true in zip(X_test, y_test):
        scores = np.dot(x, eigen_vector) @ w.T + b
        y_pred = np.argmax(scores)
        y_correct += (y_pred == y_true)

    print('Acc: %.3f' % (y_correct / len(y_test)))



if __name__ == '__main__':
    test01()
    test02()

3.2 降维计算

LDA 是一种有监督的降维技术：

• LDA 寻找一个 类间距离足够大，类内更加集中 的投影空间
• 当进行分类时，会将原始数据投影到该空间进行分类计算，此时并不关心投影的维度，一般保留原始数据维度大小
• 当进行降维时，会将原始数据投影到该空间中最重要的 N 个方向上，这里重要指的是，该方向更有利于区分不同类别的数据

前面计算投影空间时，得到的 eigen_value、eigen_vector 表示的含义：

• eigen_value：表示投影的方向的重要，该值越大，说明在这个方向上的投影越能区分不能类别的数据
• eigen_vector：表示真正的投影方向，通过 eigen_value 的降序排列，使得越重要的投影方向越靠前

最后，我们将原始数据投影到 eigen_value 最大的前 N 个 eigen_vector 的方向，就可以实现降维。

import numpy as np
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from scipy import linalg


X, y = make_classification(n_samples=100, n_features=5, n_informative=5, n_redundant=0, n_classes=3, random_state=42)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)


def test01():
    estimator = LinearDiscriminantAnalysis(solver='eigen', n_components=2)
    estimator.fit(X_train, y_train)
    X_train_transform = estimator.transform(X_train)
    print(X_train_transform)


def test02():
    # ... 得到投影空间
    # 数据降维
    n_components = 2
    X_train_transform = X_train @ eigen_vector

    X_train_transform = X_train_transform[:, :n_components]
    print(X_train_transform)


if __name__ == '__main__':
    test01()
    print()
    test02()