高斯分布（Gaussian distribution），也叫正态分布，是数据分析和统计学中最常见的一种概率分布。它得名于德国数学家卡尔·高斯，因其呈现一个对称的“钟形”曲线，因此也被称为“钟形曲线”或“钟形分布”。

• 均值为 0，标准差为 1
• 均值为 2，标准差为 1
• 均值为 0，标准差为 2

1. 概念

高斯分布是描述大量随机数据的一种数学模型。在这个分布中，数据会集中在某个值的附近，离这个值越远，出现的概率就越低。一个典型的高斯分布曲线左右对称，曲线的峰值对应数据最常出现的位置（即平均值），而两边逐渐下降，表示越偏离平均值，出现的概率越低。

例如，在一所学校的考试中，大部分学生的成绩集中在一个平均值左右，而极高分或极低分的学生通常是少数。分数的分布情况通常符合高斯分布：大多数人集中在中间少数人分布在两端。

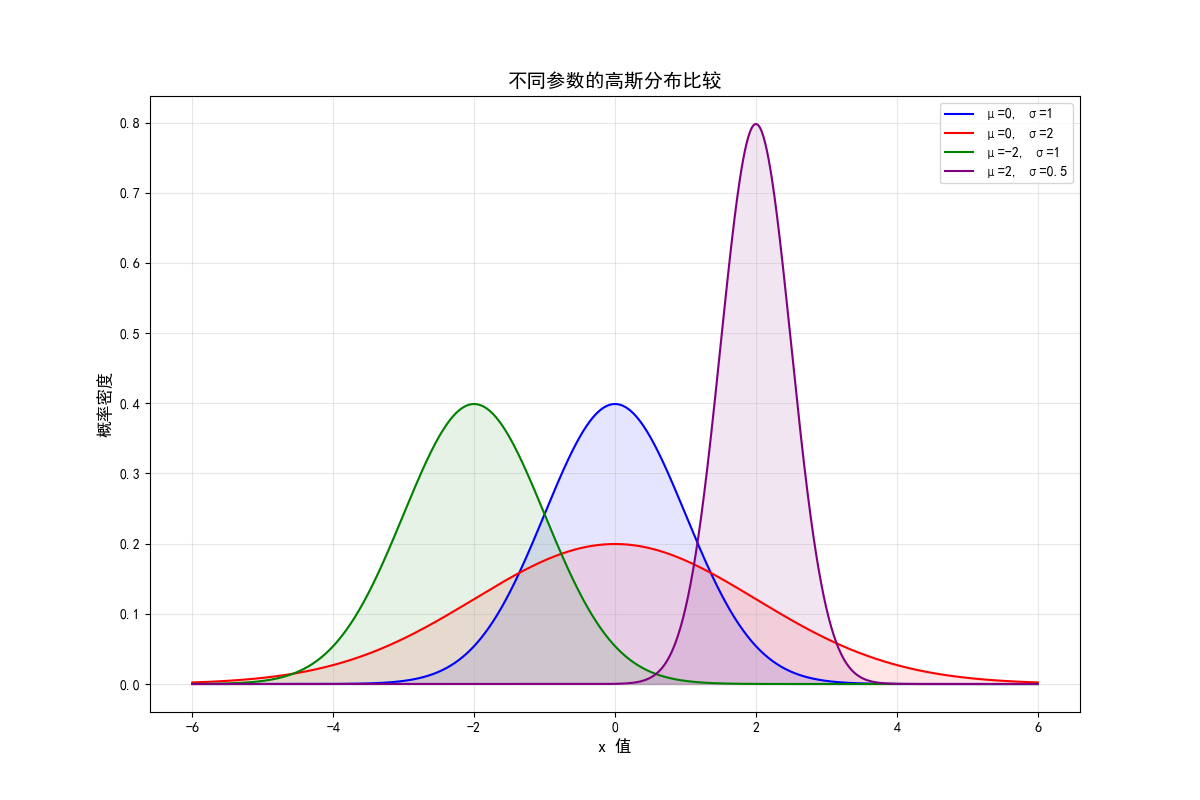
高斯分布有两个核心参数：均值（mean）和标准差（standard deviation）。

• 均值：表示数据的平均值。对于高斯分布，它位于曲线的中心，体现了数据集中分布的位置。
• 标准差：表示数据的离散程度。标准差越大，数据分布就越宽，钟形曲线就越平缓；标准差越小，数据分布越集中，曲线就越窄。

拿身高举例。假设一群人的平均身高是170厘米，标准差是5厘米，这意味着大多数人的身高会落在170±5厘米之间（即165到175厘米）。如果标准差更小，意味着大家的身高更接近平均值；如果标准差更大，身高的差异性就更明显。

为什么高斯分布如此重要？

高斯分布在很多领域中广泛应用，原因在于它符合许多自然现象。例如：

• 生物学：许多生理指标（如身高、体重、血压等）在群体中呈高斯分布。
• 心理学：智商分布通常也近似高斯分布，大多数人的智商集中在平均水平，极高或极低智商的人较少。
• 工程和质量控制：高斯分布用于检测产品质量的波动性。假设一个工厂生产某种零件，每个零件的尺寸应该接近理想值，但允许一定的偏差。质量控制员可以利用高斯分布来分析偏差数据，从而确定生产过程是否稳定。

高斯分布因为它的简单和普遍性，成为统计学和机器学习中的一个重要概念。无论是在生活中的观察，还是在数据分析的实践中，我们都可以看到高斯分布的影子。理解了这个概念，可以让我们更好地分析和解释数据，从而更准确地预测和决策。

2. 公式

下面是一元、多元高斯分布的概率密度函数。

2.1 一元高斯分布

其中：

• \( x \)是变量的取值。
• \( μ \) 是均值，表示数据集中分布的位置。
• \( σ \) 是标准差，表示数据的分散程度。

指数部分：决定数据分布形状的关键部分。它描述了每个 xxx 与均值 μ\muμ 的距离，以及这个距离对数据概率的影响。距离 μ\muμ 越近的值，指数值越接近1，表示概率大；离均值越远，指数值越小，概率也就越小。

系数部分：是一个归一化系数，用于保证整个分布的面积为1，即所有可能出现的概率总和为1。

2.2 多元高斯分布

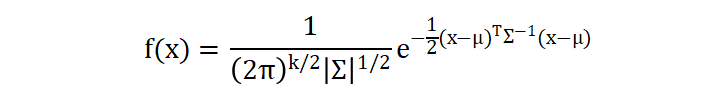
其中：

• \( x \) 是 k-维变量向量（例如，二维变量 x=[x1,x2]）。
• \( μ \) 是 k-维均值向量，表示每个变量的均值。
• \( Σ \) 是协方差矩阵，描述各变量之间的关系。
• \(∣Σ∣ \) 是协方差矩阵的行列式，影响分布的形状和大小。
• \( Σ^{-1} \) 是协方差矩阵的逆矩阵，用于描述变量之间的相互关系。

指数部分：描述了 x 距离均值向量 μ 的远近程度。协方差矩阵 Σ 决定了变量之间的关系，比如两个变量是正相关还是负相关。这个部分可以理解为多元变量在空间上距离均值的“相对距离”，距离越远，概率越小。

系数部分：是归一化系数，使得分布的总概率为1。