Batch Normalization（BN）主要解决的是内部协变量偏移（Internal Covariate Shift）问题。该问题指的是深度神经网络在训练过程中，每一层的输入分布会随着前面层参数的更新而变化，从而导致训练不稳定和收敛速度变慢。

具体来讲，每层的输入分布随着训练过程不断变化，使得网络中的每一层都需要不断地适应新的输入分布，从而使得训练过程变得不稳定（参数更新幅度较大），也需要更多的训练时间来适应这些变化，从而导致训练的收敛速度较慢。

Batch Normalization 通过对每一层的输入进行标准化（使其均值接近 0，方差接近 1），减少了输入分布的变化。这使得每一层的输入分布保持稳定，进而提高训练过程的稳定性。

1. BN 计算公式

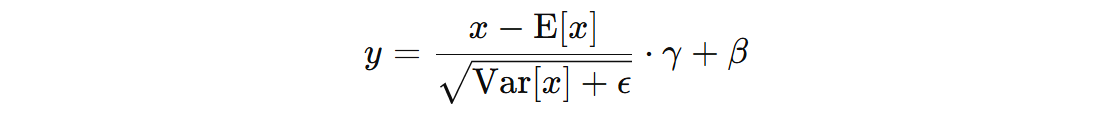
1. \( x \) 表示输入数据（训练时是一个批次的样本）
2. \( E[x] \) 表示输入数据 \( x \) 的均值
3. \( Var(x) \) 表示输入数据 \( x \) 的方差
4. \( \epsilon \) 是一个小常数 1e-5，用于避免除以零的情况
5. \( \gamma \) 是学习参数，用来控制标准化后的数据的尺度。该参数会通过反向传播进行更新
6. \( \beta \) 是学习参数，用来控制标准化后的数据的平移（数据的均值调整）。该参数也会通过反向传播进行更新

经过 BN 后输入数据的分布调整为均值为 0，方差为 1，然后再通过 \( \gamma、\beta \) 参数对数据分布进行调整，使得网络能够根据数据的特性、适应不同的输入分布，从而进行更合适的学习，提高训练稳定性并加速收敛。

在 CNN 中，BN 被广泛应用于卷积层后，以加速训练，稳定网络的学习过程，尤其是在处理复杂的图像数据时。在全连接层后使用 BN，可以有效改善训练速度，减少训练过程中出现的梯度问题。

另外，BN 通常在激活函数之前使用，即：对卷积层、线性层的输出进行 BN 操作之后，再送入到激活函数。这是因为激活函数的作用是引入非线性，使得神经网络能够学习复杂的模式和函数。如果 BN 在激活函数之后执行，它会在已经非线性的输出上进行标准化，这可能破坏网络的表达能力和非线性特性，影响模型的学习能力。

2. BN 使用示例

PyTorch 中提供了三种用于不同输入形状数据的 BN 实现，常用的两种如下：

torch.nn.BatchNorm1d(num_features, eps=1e-5, momentum=0.1, affine=False, track_running_stats=True)
torch.nn.BatchNorm2d(num_features, eps=1e-5, momentum=0.1, affine=False, track_running_stats=True)

• num_features：对于 (batch_size, input_dim) 这种批次的普通数据，对应 input_dim。而对于 (batch_size, channels, height, width) 这种批次图像数据，对应的是 channels。
• affine：如果设置为 True，则该层会有两个可训练的参数：gamma 和 beta。如果为 False，则层没有这些参数，直接使用标准化后的输出。
• track_running_stats：如果设置为 True，在训练期间，批量归一化会计算并维护当前批次的均值和方差的滑动平均，以便在推理（评估）阶段使用。如果设置为 False，则不计算这些统计信息。
• momentum：用来更新 BN 中的 running_mean 和 running_var 的系数。

running_mean 和 running_var 的更新公式：

running_mean = (1 - momentum) * running_mean + momentum * batch_mean
running_var  = (1 - momentum) * running_var  + momentum * batch_var

注意，BN 在实际应用时，分为训练模式和推理模式（track_running_stats=True）：

• 训练模式：会累计均值和方差的滑动平均，但是计算时使用 batch_mean 和 batch_var
• 推理模式：不会累计均值和方差，在计算时使用 running_mean 和 running_var

下面为两个 API 的使用示例代码：

import torch
import torch.nn as nn


def test01():
    bn = nn.BatchNorm1d(num_features=5, eps=1e-5, momentum=0.1, affine=False, track_running_stats=True)
    bn.train()

    # 数据形状 (batch_size, input_dim)
    data = torch.rand(size=(10, 5))
    data = torch.split(data, 5)

    for batch_inputs in data:
        outputs = bn(batch_inputs)
        print('均值:', bn.running_mean, '方差:', bn.running_var)

    # 推理时，会使用累计的均值和方差进行计算
    bn.eval()
    output = bn(torch.rand(size=(1, 5)))
    print(output)


def test02():
    bn = nn.BatchNorm2d(num_features=3, eps=1e-5, momentum=0.1, affine=False, track_running_stats=True)
    bn.train()

    # 数据形状 (batch_size, channels, height, width)
    data = torch.rand(size=(6, 3, 2, 2))
    data = torch.split(data, 2)

    for batch_inputs in data:
        outputs = bn(batch_inputs)
        print('均值:', bn.running_mean, '方差:', bn.running_var)

    bn.eval()
    output = bn(torch.rand(size=(1, 3, 2, 2)))
    print(output)


if __name__ == '__main__':
    test01()
    print('-' * 30)
    test02()

程序执行结果：

均值: tensor([0.0571, 0.0544, 0.0531, 0.0600, 0.0437]) 方差: tensor([0.9009, 0.9079, 0.9060, 0.9097, 0.9031])
均值: tensor([0.0950, 0.1010, 0.0722, 0.1169, 0.0945]) 方差: tensor([0.8237, 0.8247, 0.8245, 0.8306, 0.8159])
tensor([[-0.0235,  0.3534,  0.7883,  0.0882,  1.0016]])
------------------------------
均值: tensor([0.0486, 0.0496, 0.0545]) 方差: tensor([0.9096, 0.9051, 0.9135])
均值: tensor([0.1084, 0.0850, 0.1127]) 方差: tensor([0.8259, 0.8194, 0.8302])
均值: tensor([0.1290, 0.1263, 0.1426]) 方差: tensor([0.7495, 0.7419, 0.7561])
tensor([[[[ 0.7845,  1.0046],
          [ 0.3233,  0.4021]],

         [[ 0.0600,  0.4899],
          [-0.0521, -0.0421]],

         [[ 0.8965,  0.7647],
          [ 0.1038,  0.8081]]]])

最后，再补充下，对于两种不同数据的批次均值和方差的计算：

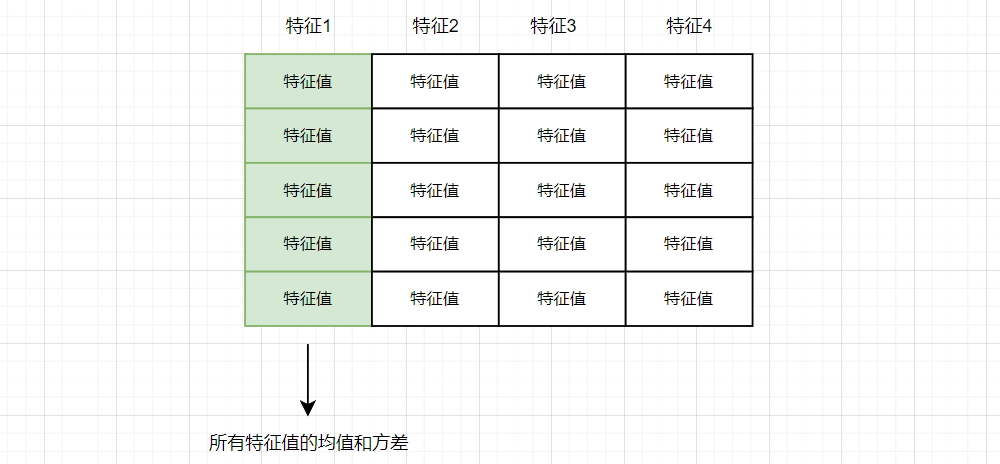
对于 (batch_size, input_dim) 形状的数据，均值和方差是以特征为单位进行计算，将所有该批次内某个特征所有的值当做一个序列，来计算该批次的均值和方差。

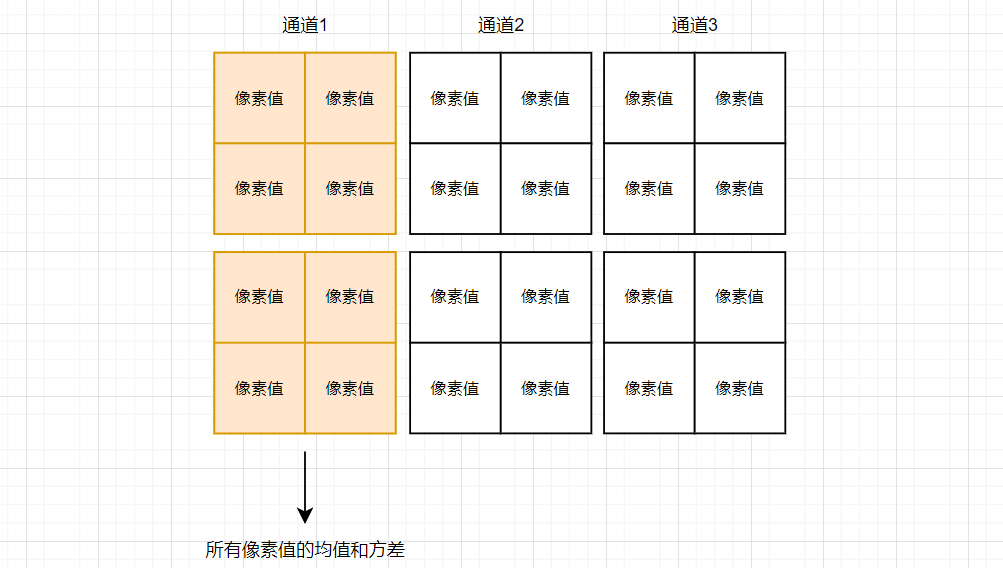
对于 (batch_size, channels, height, width) 形状的数据，均值和方差是以通道为单位进行计算，将一个批次中所有该通道的特征图中所有的像素值当做一个序列数据 (像素值, 像素值... 像素值)，计算该批次的均值和方差。