XGBoost(Extreme Gradient Boosting)2014 年由陈天奇开发,旨在对传统梯度提升算法(GBDT)进行高效实现和优化。2015 年,XGBoost 在 Kaggle 竞赛中表现卓越,多个冠军队伍使用了 XGBoost,横扫众多榜单。凭借卓越的性能和广泛的适用性,XGBoost 很快成为竞赛和工业界的标配算法,被广泛应用于金融风控、推荐系统、广告点击率预测、科研建模等领域。
文档:https://xgboost.readthedocs.io/en/stable
论文:https://arxiv.org/pdf/1603.02754
1. 优化思路
在传统 GBDT 中,模型每一棵树的目标就是降低训练误差,但这种训练方式存在两类结构性问题:树结构不受约束,以及叶子输出容易数值不稳定。XGBoost 的核心创新,正是系统性地重写这两类复杂度,让模型既能更稳,也能更准。
1.1 结构复杂度
传统 GBDT 训练时,每棵树都会不断分裂节点来降低训练误差。分裂越多,叶子覆盖的样本越少,极端情况下,一个叶子只覆盖一个样本,训练误差几乎为零,完全贴合训练数据,导致过拟合。
常见做法是给树设上硬性限制,比如最大深度或叶子数量,用来阻挡过度生长。问题在于这些限制太粗暴:
- 有些分裂虽然会让树变深,但带来的误差下降非常可观,却因为触碰到超参数上限而被硬拦下来。
- 有些分裂虽然能带来一点点误差下降,但相比它增加的模型复杂度,其价值并不高,却因为没有触发限制而被轻易放行。
理想的方式是:每次分裂都既看误差是否下降,也看结构复杂度是否值得增加。这样,高价值分裂自然被保留,价值低的分裂自然熄火。硬性超参数退到“保底位”,只在模型真的往失控方向冲时介入,而不干扰正常的分裂选择。
XGBoost 正是沿着这个思路引入了结构复杂度正则项。它把新增叶子的复杂度直接放进目标函数里。一次分裂能不能通过,不只看损失下降多少,而要看收益能否抵消复杂度成本。如果划不来,这次分裂就被拒绝。
有了这套机制,树的生长从“被外力限制”变成“在优化中自我调节”。模型既能保留真正有意义的结构,又能避免无效膨胀,从而得到更合理、灵活且泛化更强的树。
1.2 输出复杂度
传统 GBDT 在确定叶子节点的输出时,会直接根据节点中样本的一阶导数和二阶导数计算更新量:
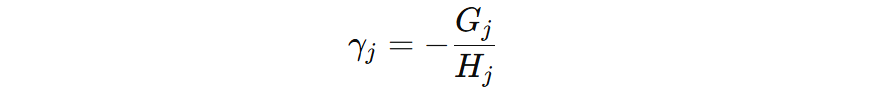
然而在许多任务中,尤其是分类问题,叶子节点上的二阶导可能非常小,甚至接近于零。当二阶导过小,叶子节点的更新值会被异常放大,从而导致模型对该叶子所覆盖样本做出不合理的大幅度预测调整。假设某个叶子里 \(G_{j} = -10\),而 \(H_{j}=0.01\),则 \(\gamma_{j} = 1000\)。
这样不仅可能破坏损失下降的趋势,还会让训练进入震荡和不稳定的状态,使得后续树被迫不断修补前一棵树的误差,整体优化过程随之恶化。
XGBoost 在目标函数中引入了叶子输出的 L2 正则化,通过对叶子输出值施加惩罚,使得叶子节点的输出值被进一步平滑化,使得模型的更新不会因局部不稳定的梯度而出现极端值,同时也提升了整体优化的可控性。
2. 公式推导
XGBoost 训练的核心是逐棵构建决策树,而每棵树的训练需要解决两个关键问题:如何进行节点分裂,以及如何确定叶子节点的输出值。
在训练过程中,XGBoost 需要同时兼顾训练误差和模型复杂度。传统的 square error 或 friedman mse 等分裂增益计算方法,无法直接满足这种联合优化的需求。因此,必须基于损失函数的优化目标,推导出适用于 XGBoost 的分裂增益计算逻辑。
同样地,树构建完成后,叶子节点的输出值也不能通过简单规则确定。其最优解需结合具体损失函数的特性,通过公式推导得到相应的计算方法。
简言之,公式推导的目的就是明确:分裂增益的计算方法,以及叶子节点输出的最优计算方法。
2.1 目标函数
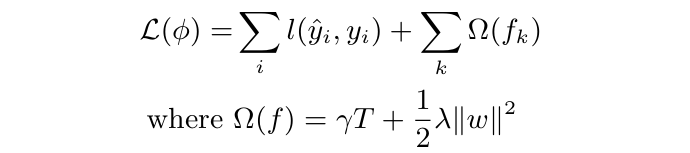
一部分衡量模型在训练集上的拟合情况(训练误差),另一部分惩罚模型复杂度(正则项)。
- \( \gamma T \):表示对叶子节点数量的惩罚,\(\gamma\) 越大说明分裂一次带来的复杂度更大,越希望模型更加简单。
- \( \frac{1}{2}\lambda \|w\|^2 \) 表示对模型输出的惩罚。\(\lambda\) 越大说明越希望模型输出保守一些。
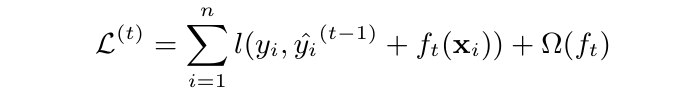
由于 \( l(y_i, \hat{y}_{i}) \) 可能是任意复杂的非线性函数,并且,我们要优化的 \( f_{m}(x) \) 是整个损失函数内部的一部分,直接对 \( f_{m}(x) \) 优化不现实。所以,我们需要使用泰勒二阶展开这个工具将损失函数近似成一个关于 \( f_{m}(x) \) 的二次函数,这样就能继续优化。
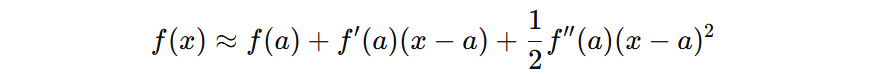
- a 表示截止到 m-1 树时的模型输出值
- x 表示截止到 m 树时的模型输出值
- x−a 表示第 m 棵树带来的模型输出增量
- f(a) 表示截止到第 m-1 棵树时,模型的损失函数值
- f′(a) 表示损失函数在 a 处对模型输出的一阶导数
- f′′(a) 损失函数在 a 处对模型输出的二阶导数
我们对损失函数在 \( t-1 \) 处进行泰勒二阶展开,通过损失函数在该处的损失、以及一阶导和二阶导信息,得到近似的损失表示:
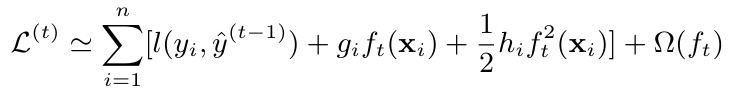
- \( g_{i} \) 表示样本的一阶导
- \( h_{i} \) 表示样本的二阶导
\( l(y_i, \hat{y}^{t-1}) \) 表示还没有加入新树时的损失,这一项是常数项,可以去掉,我们就得到了一个关于 \( f_{t}(x_{i}) \) 的公式:
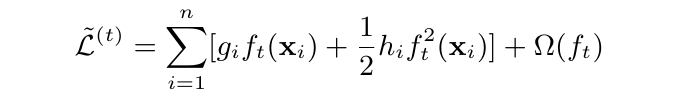
我们希望知道新树 \(f_{t}\)如何如何输出,才能使得损失最小。为了能够得到新树的最优输出,我们需要将上面的目标函数转换到叶子节点角度表示的形式:
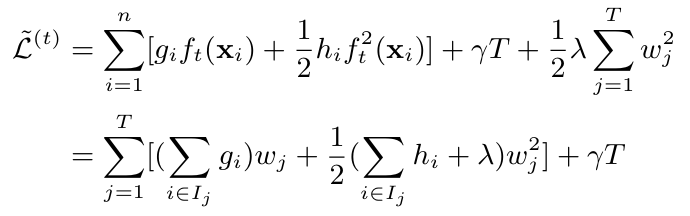
注意:上述公式中,\( w \) 表示叶子节点的输出值。
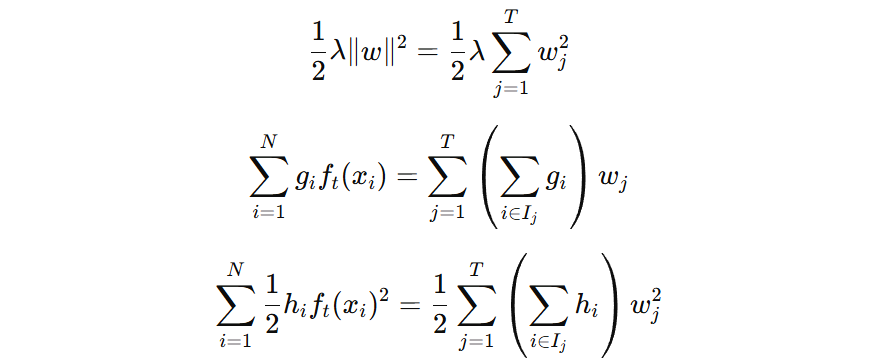
对 \( w \) 求导,并令导数等于 0,得到叶子节点最优输出值表示:
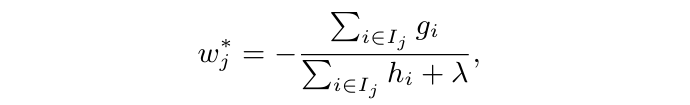
注意:\(\lambda\) 最初是损失函数中正则化项的系数,经过推导,最终体现在上公示中的分母部分。回顾前面例子,当 \(G_{j} = -10\)、\(H_{j}=0.01\)、\(\lambda = 1\),则 \(w_{j} = 9.9\),输出值显著降低,避免了输出爆炸式的极端情况。
此时,将叶子节点输出值公式代回到原公式中,得到在最优输出的情况下的损失表示:
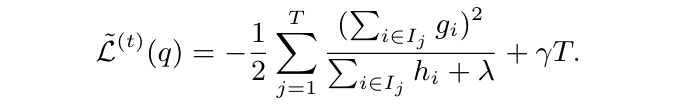
再简化下上面公式的表示:
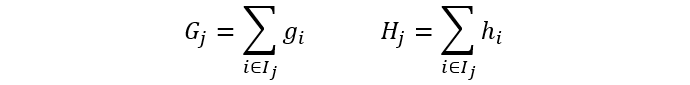
\( G_{i} \) 表示叶子结点上一阶导之和,\( H_{i} \) 表示叶子结点上的二阶导之和。
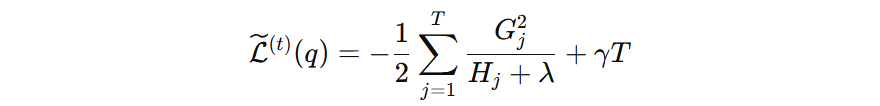
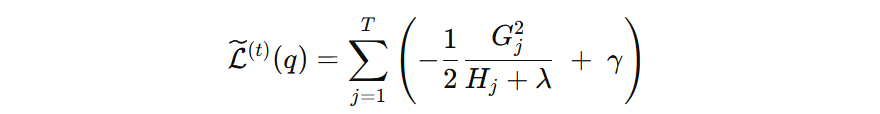
公式中:第一项表示这个叶子节点在最优输出值下能带来的损失下降。第二项表示这个叶子节点自身的复杂度成本。
- 如果公式的值为 负值,说明该叶子节点带来的损失下降大于它增加的复杂度惩罚,对目标函数有利,有助于下降。
- 如果公式的值为 正值,说明该叶子节点带来的损失下降不足以抵消复杂度惩罚,它的存在反而会让目标函数上升。
换句话说,这个值衡量了每个叶子节点对目标函数的贡献。如果一个叶子节点能带来的损失下降(第一项)不足以抵消它的复杂度成本(第二项),那么这个叶子的存在会让整体目标函数变大,不应该被保留。
2.2 分裂增益
单个叶子节点对目标函数的贡献(越小越好)
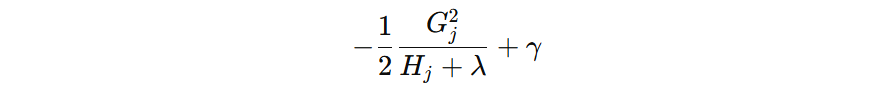
当某个节点分裂后,原节点的对目标函数的贡献就被替换为:新左节点的贡献 + 新右节点的贡献。
我们可以利用分裂前后的的差值来作为 XGBoost 的分裂增益计算方法:
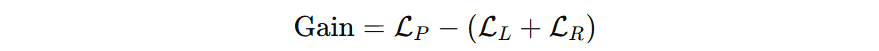
- 当 \( Gain \gt 0\),分裂前能降 -500,分裂后能降 -800,分裂后损失能多降 300,该分裂被考虑
- 当 \( Gain \leq 0\),分裂前能降 -500,分裂后能降 -300,分裂后损失能少降 200,该分裂不考虑
- Gain 越大说明,此次分裂的价值越大
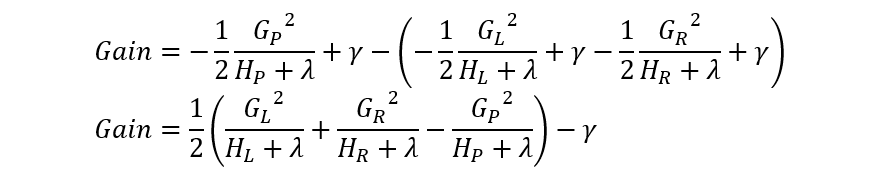
这个公式就是 XGBoost 算法的分裂增益计算公式。如果一次分裂带来的损失下降不足以抵消它的复杂度成本,此次分裂不会被考虑。
3. 计算案例
| 样本 i | x | y |
|---|---|---|
| 1 | 1 | 2.1 |
| 2 | 2 | 4.0 |
| 3 | 3 | 6.2 |
| 4 | 4 | 8.1 |
| 5 | 5 | 10.0 |
| 6 | 6 | 12.2 |
| 7 | 7 | 14.1 |
| 8 | 8 | 16.0 |
| 9 | 9 | 18.1 |
| 10 | 10 | 20.2 |
损失函数:平方损失,λ = 1, γ = 0
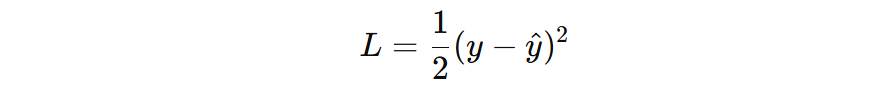
损失函数一阶导和二阶导计算公式:
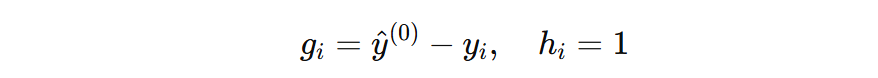
初始预测取均值:
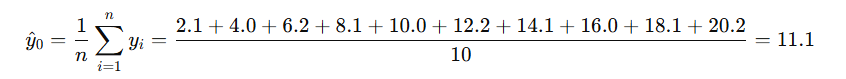
计算每个样本的一阶导和二阶导值:
| 样本 i | x | y | 基础预测 | 一阶导 | 二阶导 |
|---|---|---|---|---|---|
| 1 | 1 | 2.1 | 11.1 | 9.0 | 1 |
| 2 | 2 | 4.0 | 11.1 | 7.1 | 1 |
| 3 | 3 | 6.2 | 11.1 | 4.9 | 1 |
| 4 | 4 | 8.1 | 11.1 | 3.0 | 1 |
| 5 | 5 | 10.0 | 11.1 | 1.1 | 1 |
| 6 | 6 | 12.2 | 11.1 | -1.1 | 1 |
| 7 | 7 | 14.1 | 11.1 | -3.0 | 1 |
| 8 | 8 | 16.0 | 11.1 | -4.9 | 1 |
| 9 | 9 | 18.1 | 11.1 | -7.0 | 1 |
| 10 | 10 | 20.2 | 11.1 | -9.1 | 1 |
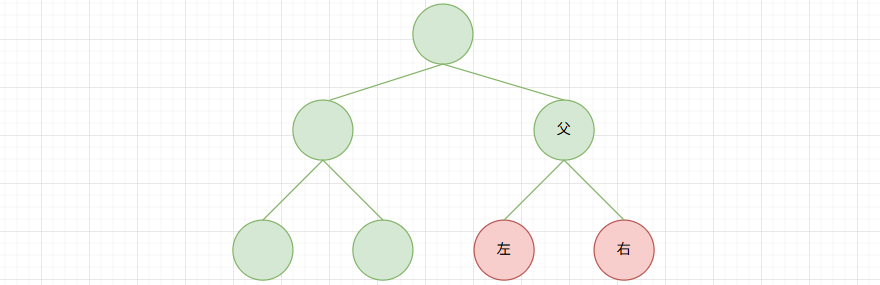
我们以分裂点 x < 6 为例,计算下其分裂增益:
| 节点 | 样本集合 | 一阶导和 (G) | 二阶导和 (H) |
|---|---|---|---|
| 左子集 | (1, 2, 3, 4, 5) | 25.1 | 5 |
| 右子集 | (6, 7, 8, 9, 10) | -25.1 | 5 |
| 父节点 | 所有样本 | 0 | 10 |
带入到分裂增益计算公式中:
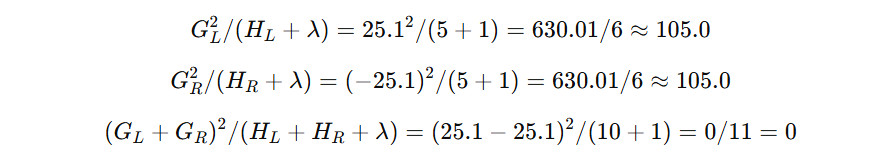
Gain = 0.5 ∗ (105.0 + 105.0 − 0)−0 = 0.5 ∗ 210.0 = 105.0
最后计算下叶子节点的输出值:
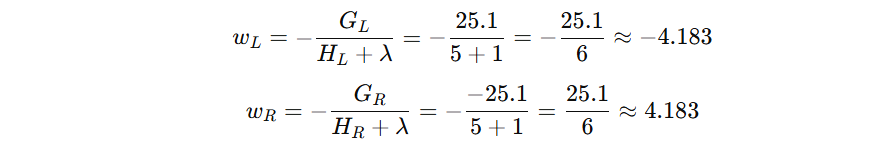
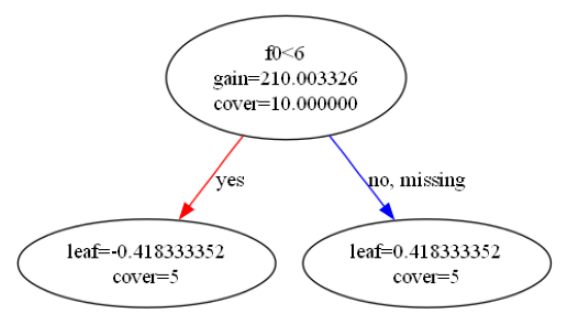
# pip install scikit-learn
# pip install xgboost
# pip install matplotlib
from xgboost import XGBRegressor, plot_tree
import numpy as np
import matplotlib.pyplot as plt
def demo():
# 构造数据
x = np.array([1,2,3,4,5,6,7,8,9,10]).reshape(-1,1)
y = np.array([2.1,4.0,6.2,8.1,10.0,12.2,14.1,16.0,18.1,20.2])
# 训练模型
xgb = XGBRegressor(n_estimators=2, max_depth=2, learning_rate=0.1, objective='reg:squarederror')
xgb.fit(x, y)
# 绘制每棵树
for idx in range(xgb.n_estimators):
plt.figure(figsize=(12,8), dpi=150) # 调整图像大小和分辨率
plot_tree(xgb, tree_idx=idx, rankdir='LR', with_stats=True) # 'LR' 横向展示
plt.show()
xgb.predict
if __name__ == '__main__':
demo()




 冀公网安备13050302001966号
冀公网安备13050302001966号