回归分析是统计学中用于预测连续型数据的一种方法。常见的回归模型包括线性回归和多项式回归。多项式回归是线性回归的扩展，它能够处理更复杂的数据关系。

线性回归假设因变量与自变量之间存在线性关系。对于一些非线性的数据，线性回归无法提供良好的拟合效果，这时就需要引入多项式回归。

1. 原理

多项式回归通过对原始特征进行扩展，可以得到新的特征。例如，对于二次回归，我们可以将每个特征 \( x \) 扩展为：

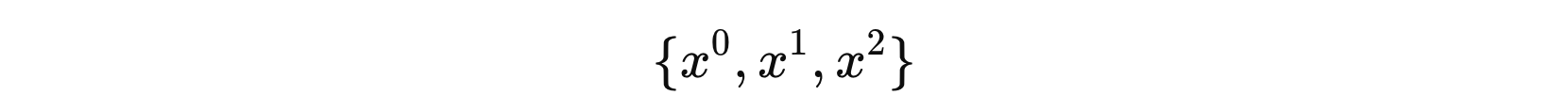
Scikit-Learn 中的 PolynomialFeatures 类提供了方便的功能来实现这一点。使用 LinearRegression 或者 SGDRegressor 在扩展后的特征数据集上最小化误差平方和，就实现多项式回归。

多项式回归并不是一个独立的回归算法，而是通过对原始特征进行多项式扩展（特征工程或特征增强）后，应用线性回归算法对扩展后的特征进行建模，从而能够捕捉数据中的非线性关系。

2. 使用

import numpy as np
import sympy
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures


def poly_regression(degree):
    """degree 为最高此项"""

    x = [-10., -7.78, -5.56, -3.33, -1.11, 1.11, 3.33, 5.56, 7.78, 10.]
    y = [107., 69.49, 31.86, 11.11, -0.77, 4.24, 20.11, 29.86, 59.49, 95.]

    # 绘制散点图
    plt.scatter(x, y)

    # 将列表 x、y 转换为矩阵，并转置
    x = np.mat(x).transpose()
    y = np.mat(y).transpose()

    # 构建多项式特征, degree 指定最高此项
    x = PolynomialFeatures(degree=degree, include_bias=False).fit_transform(x)

    # 线性回归对象
    linear_model = LinearRegression()
    linear_model.fit(x, y)

    # 构建多项式方程
    x = sympy.Symbol("x")
    items = []
    ratio_list = linear_model.coef_[0]
    for i, w in enumerate(ratio_list):
        items.append(w * x ** (i + 1))

    y = sum(items) + linear_model.intercept_[0]

    x = np.linspace(-10, 10, 10)
    y = [y.subs({"x": v}) for v in x]

    # 绘制折线
    plt.plot(x, y)
    plt.show()


if __name__ == "__main__":

    poly_regression(1)
    poly_regression(3)
    poly_regression(5)
    poly_regression(8)

程序执行结果为：

随着 degree 的变大，拟合效果越来越好。但是，并不是最高此项越高，拟合效果就一定越好。