GBDT 的全称是 Gradient Boosting Decision Tree，是 Boosing 算法思想的一种实现，是最速下降法与前向加法模型的结合。训练时，通过拟合损失函数的负梯度来逐步优化损失函数，得到每一个弱学习器。GDBT 无论解决分类问题，还是回归问题都是用 CART 回归树。

GBDT 用于回归问题可使用多种损失函数，我们以最常用的平方损失函数为例。

1. 问题解决思想

平方损失的负梯度为：

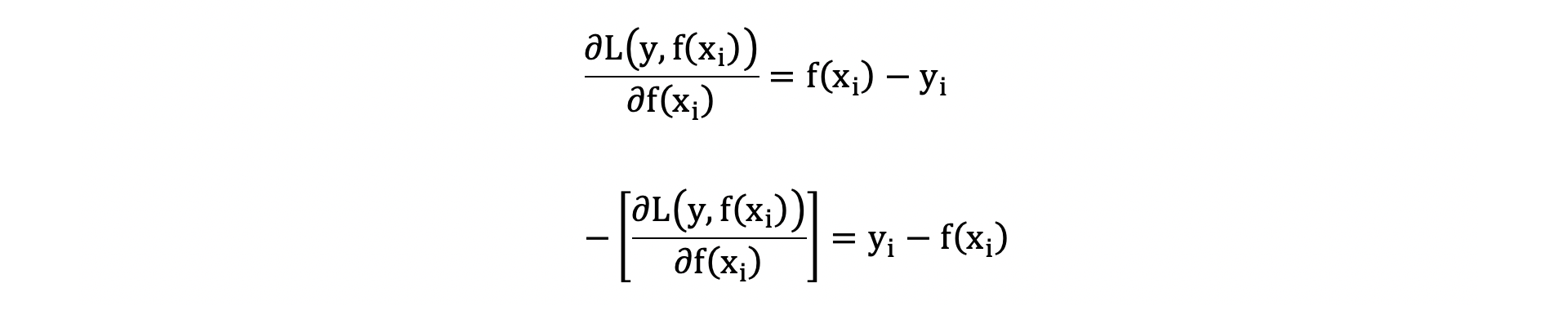
由此，我们可以得出，当前弱学习器拟合的上一个弱学习器的输出值和真实值的残差。其算法基本流程如下：

1. 初始化一棵树，类似于最速下降法要初始化参数。

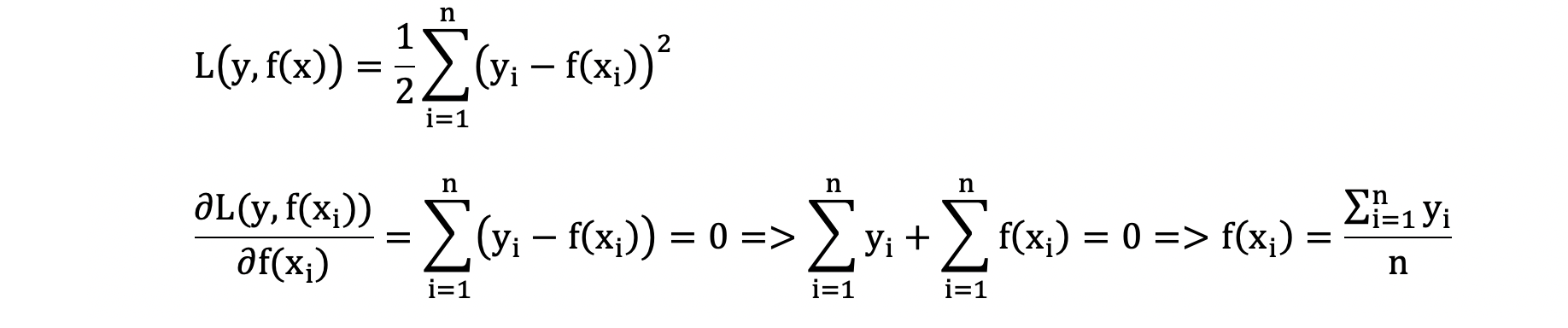
2. 修改当前树拟合的训练样本的目标值为上一棵树的真实值与输出值之间的残差，重复该过程直到构建指定个数的弱学习器。

2. 算法原理举例

梯度提升算法（GBDT）是提升算法的一种实现，它在训练每一个弱学习器的时候，沿着损失函数对之前已经训练得到的强学习器预测值的负梯度方向迭代，以此构造样本的标签值训练每一个弱学习器。

1.2.1 初始化树

我们通过计算当模型预测值为何值时，会使得第一个基学习器的平方误差最小，即：求损失函数对 f(x_i) 的导数，并令导数为0.

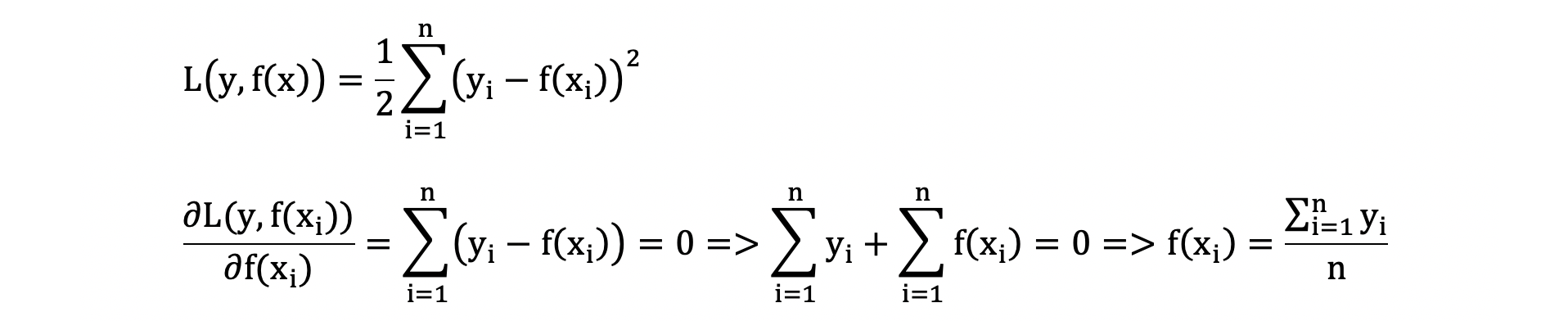
将样本代入上述公式，此时得到初始化基学习器为：

1.2.2 训练第一个基学习器(决策树)

由于我们拟合的是样本的负梯度，即：

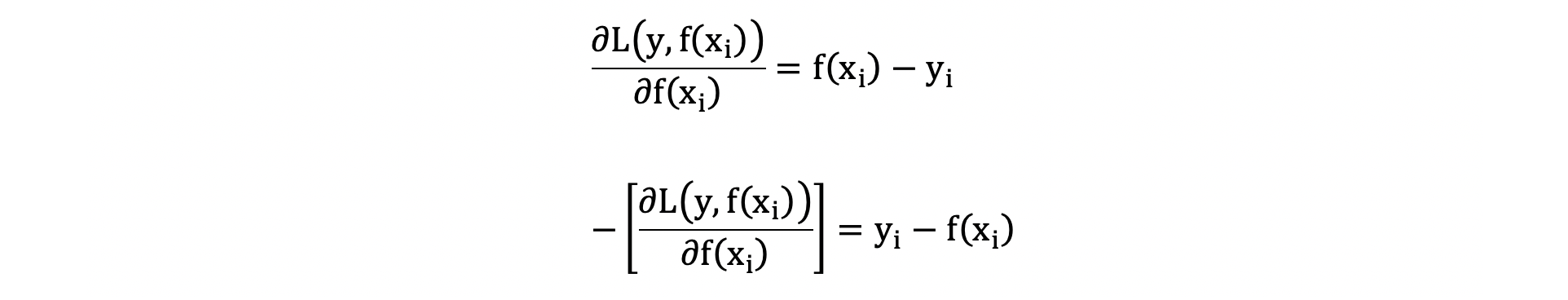
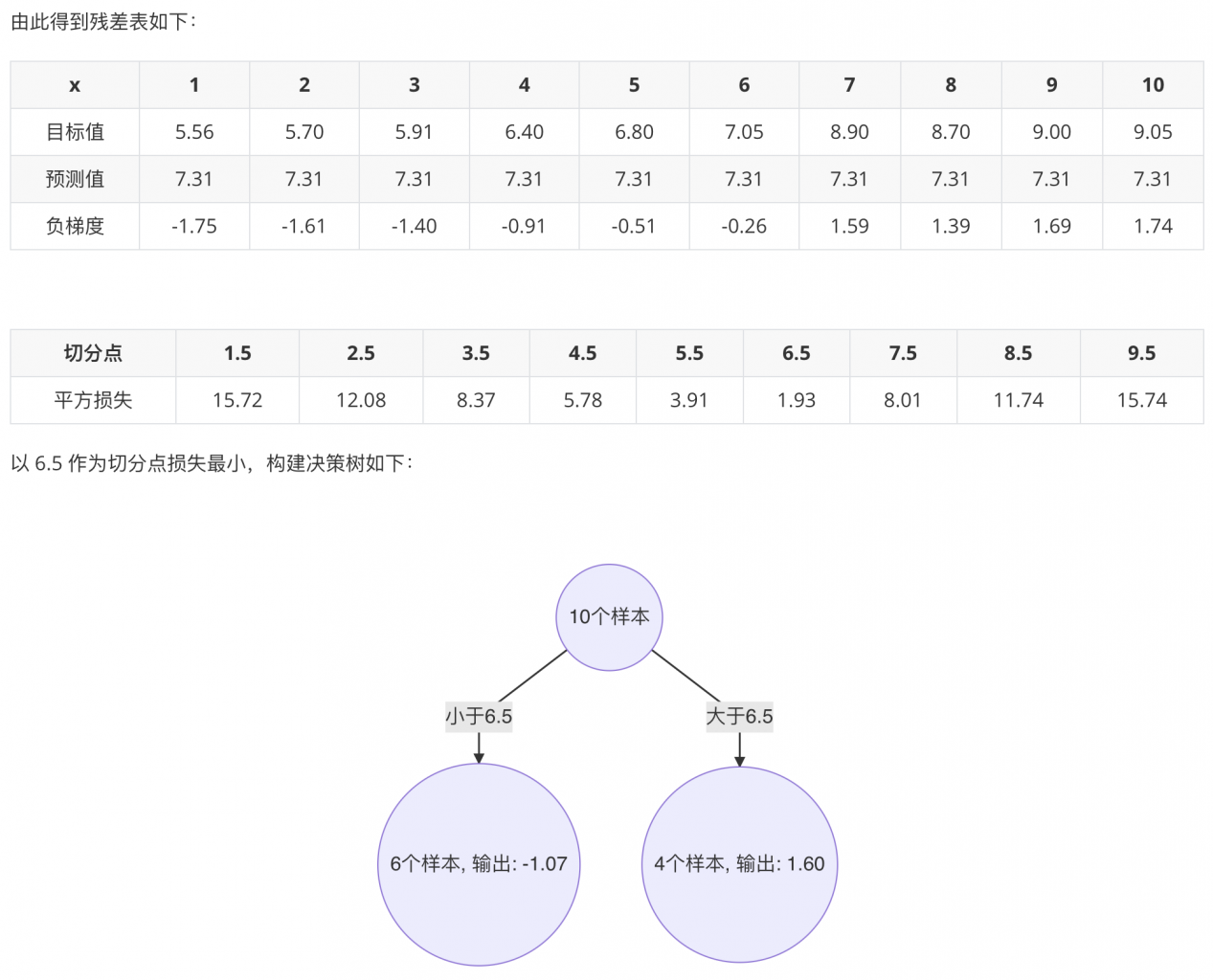
1.2.3 训练第二个基学习器(决策树)

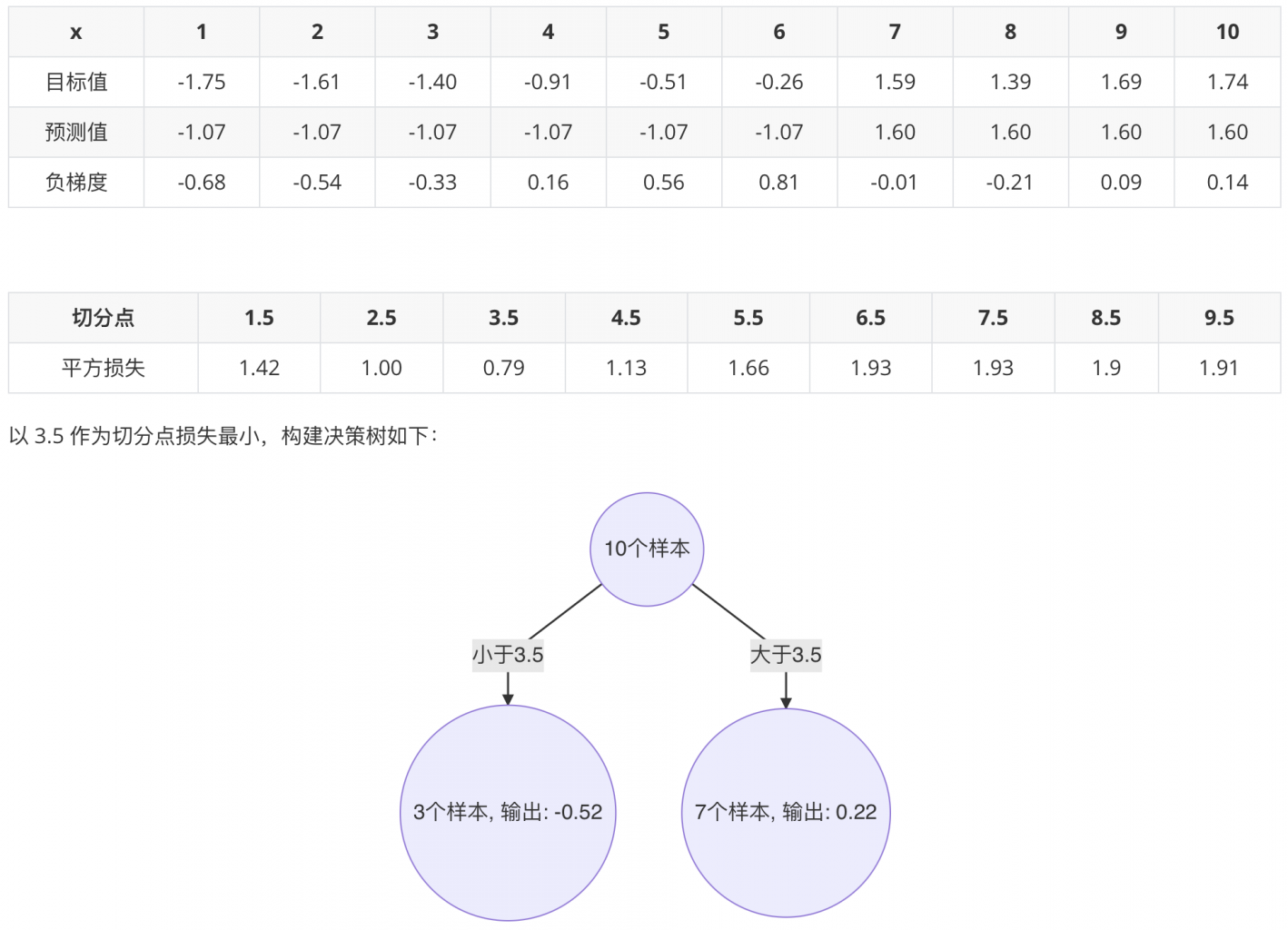
1.2.4 训练第三个基学习器(决策树)

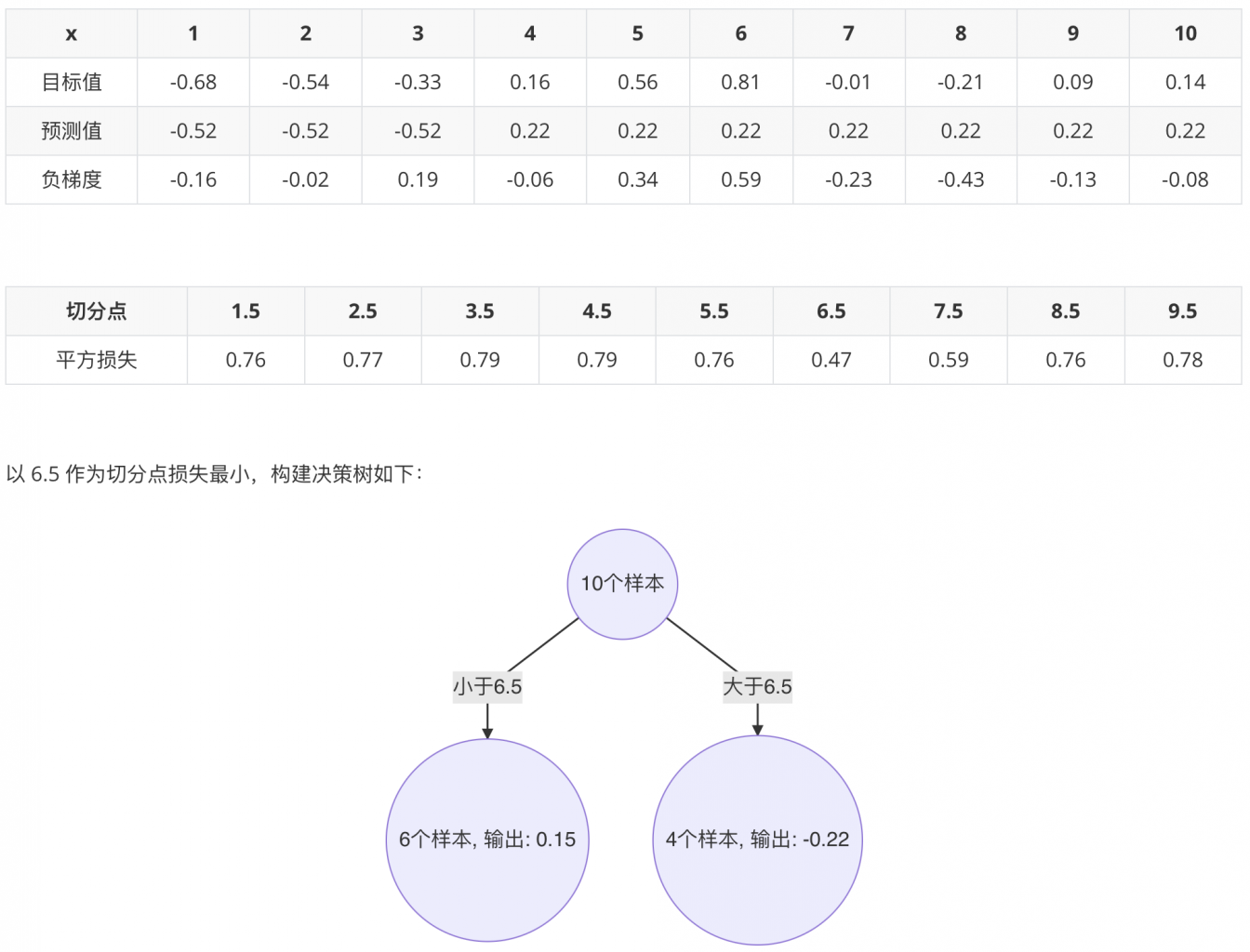
1.2.5 最终强学习器

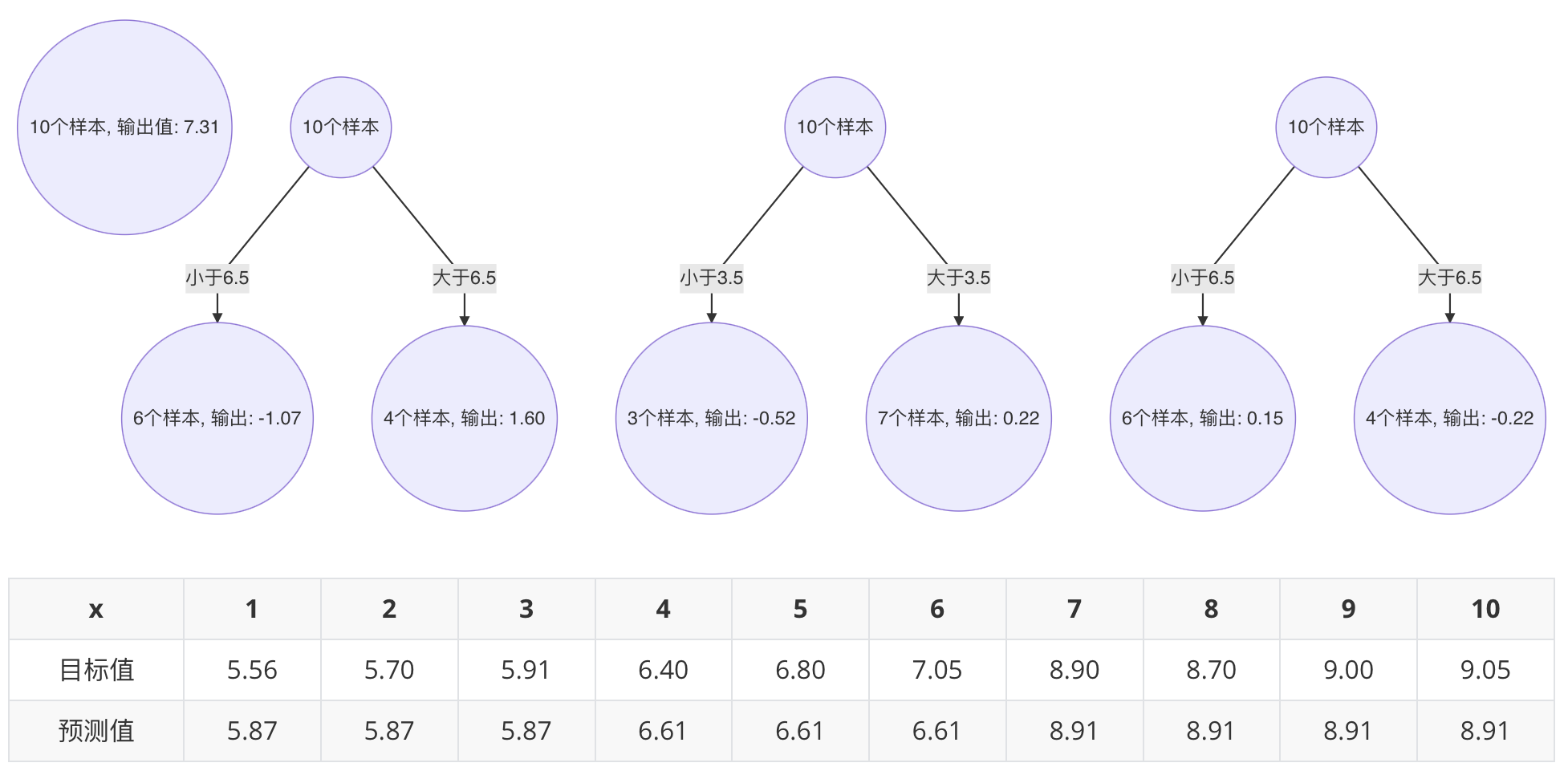
3. GBDT 的学习率

1. 学习率用来平衡树的数量、每棵树的贡献
2. 学习率越小，每棵树的贡献就越小，需要更多的树提高精度
3. 学习率越大，每棵树的贡献就越大，需要树的数量就越少