主成分分析（PCA，Principal Component Analysis）是一种常用的数据降维技术。数据降维是指将高维数据转换为低维数据的过程，同时尽可能保留原始数据的重要信息。通过降维可以：

降低计算复杂度：设你有一个数据集，包含 100 个特征。每个特征的计算都需要花费一定的时间和资源，那么处理这些数据就非常昂贵。通过降维，把这些 100 个特征降到 10 个特征，减少的特征数意味着需要处理的数据量变小，算法可以在更短的时间内完成计算，从而提高效率。
减少噪声：在高维数据中，噪声往往以随机的形式分布在各个特征上，会对模型产生一定的负面影响。降维通过保留主要的、信息量较大的特征，而去除那些冗余的、低贡献的特征，从而减少了噪声的影响。
缓解“维度灾难”：维度灾难的核心问题是，随着数据特征的增加，数据空间变得非常大，数据点之间的距离也变得非常远，导致数据变得非常稀疏。这样，算法就很难从中发现有用的规律，处理起来既慢又不准确。为了应对这个问题，我们通常通过降维（比如使用主成分分析PCA）来减少特征数量，保留最重要的信息，这样可以使算法更高效、准确地工作。

1. 基本思想

PCA 的基本思想是找到数据投影之后，方差最大的方向，从而实现对原始数据降维。比如：我们希望将 3 维空间中的手势降维到 2 维。为了能够在投影之后，保留更多的原始手势的重要信息，我就需要找到在投影后方差最大的 2 个方向。

手势在进行投影的时候，可以从各个不同的角度进行投影，得到到在 2 维平面上的手势是不同的。

如果从手势的侧面投影时，在 2 维平面上图像的信息保留更多，数据在 2 个维度上的方差也比较大
如果从手势的背面投影时，在 2 维平面上图像的信息保留相对较少，在 2 个维度上的方差也比较小

至此，大家应该能够直观的理解为什么 PCA 通过找到投影后方差最大的方向进行降维，能够更多的保留原始数据的信息。

这里需要注意的是，如果我们希望将原始数据降维到 2 维，就需要找到两个投影方向，这些投影方向就叫做主成分。方差最大的方向叫做第一主成分、方差第二大的方向叫做第二主成分，以此类推….，这些主成分表示的方向是正交的。

2. 计算过程

为了描述数据在不同方向上的方差，我们首先计算协方差矩阵 \( \Sigma \) 。协方差矩阵描述了数据集每对特征之间的线性关系以及它们各自的方差。协方差矩阵（X 已减去均值）的定义是：

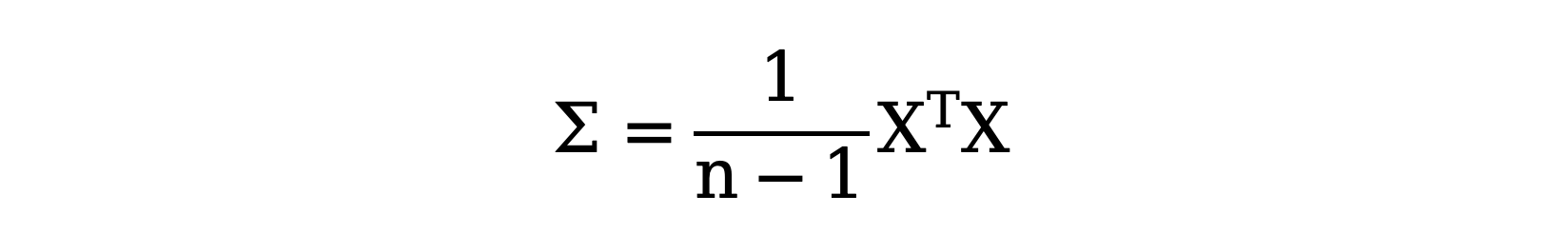
我们希望找到一个单位向量 v（也就是一个具有单位长度的向量），使得数据投影到这个向量上的方差最大。这个投影方差可以通过以下公式表示：

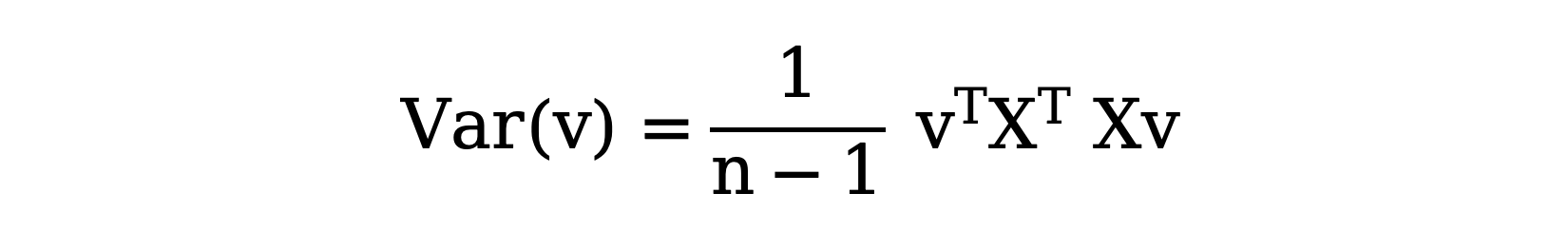
这个问题本质上是一个 优化问题，我们需要最大化以下表达式：

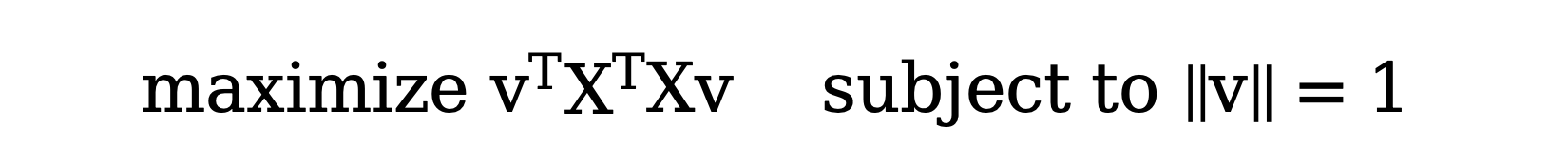
接下来，我们使用 拉格朗日乘数法 来对上面的问题进行转换：

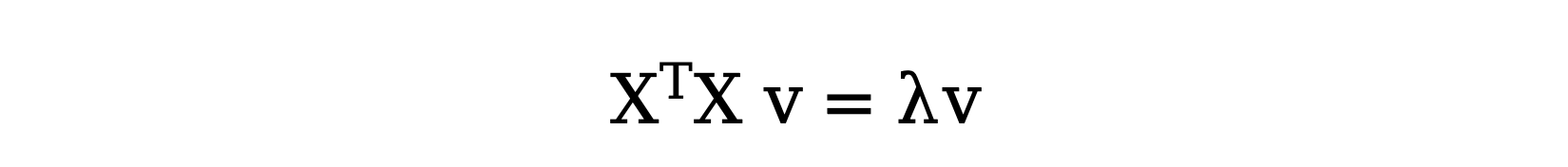
这就是一个 特征值问题，其中 v 是协方差矩阵 \( X^{T}X \) 的特征向量，λ 是对应的特征值。

from sklearn.datasets import make_classification
import numpy as np


def test():
    # 1. 生成 20 维数据
    X, y = make_classification(n_samples=100, n_features=20, random_state=42)
    print('降维前:', X.shape)


    # 2. 计算协方差矩阵
    mean = np.mean(X, axis=0)
    x_centered = X - mean
    X_cov = (x_centered.T @ x_centered) / (X.shape[0] - 1)

    # 3. 计算特征值和向量
    # eigenvalues 为特征值，eigenvectors 每一列为特征向量
    eigenvalues, eigenvectors = np.linalg.eig(X_cov)

    # 4. 获得前 n_components 个特征向量，即：主成分
    n_components = 3
    components = np.real(eigenvectors[:, :n_components])
    print('主成分:', components.shape)

    # 5. 将 X 投影到主成分实现降维
    X_transform = X @ components

    # 6. 中心化投影后的向量
    X_transform -= mean @ components

    print('降维后:', X_transform.shape)


if __name__ == '__main__':
    test()

    # 输出结果:
    # 降维前: (100, 20)
    # 主成分: (20, 3)
    # 降维后: (100, 3)

3. 参数属性

svd_solver 参数，用于计算 SVD（奇异值分解）的算法，默认 auto：

full：速度慢，精度高，适合数据规模小，要求高精度的场景
arpack：速度中等，精度中高，适合稀疏数据
randomized：速度快，精度中，适合数据规模大，对精度要求较低
auto：自动选择合适的算法，通常情况下都能有效选择

whiten 参数，是否对数据进行白化，使得每个主成分的方差都为 1。这对于某些机器学习算法很重要，尤其是当数据的尺度差异较大时，默认 False。

iterated_power、n_oversamples、power_iteration_normalizer 三个参数与 randomized 求解器相关的参数，使用默认设置即可。

scikit-learn 中的 PCA API 的 n_components 参数可以指定降维的维度，也可以指定一个小数，保留多少信息量，这个信息量就是根据 explained_variance_ratio_ 来衡量。

from sklearn.decomposition import PCA
from sklearn.datasets import make_classification
import numpy as np


def test():

    X, y = make_classification(n_samples=100, n_features=5, random_state=42)

    pca = PCA(n_components=2, whiten=True)
    X_transform = pca.fit_transform(X)

    # 特征方差
    print(np.var(X_transform, axis=0))
    print('主成分:\n', pca.components_)

    print('奇异值:\n', pca.singular_values_)
    # 特征向量（主成分）对应的特征值，值越大，越能包含更多原始数据的信息
    # 由奇异值计算特征值：pca.singular_values_ ** 2 / (X.shape[0] - 1)
    print('解释方差：',  pca.explained_variance_)
    print('解释方差比：', pca.explained_variance_ratio_)


if __name__ == '__main__':
    test()

A Tutorial on Principal Component Analysis https://arxiv.org/pdf/1404.1100

主成分分析（PCA）

1. 基本思想

2. 计算过程

3. 参数属性

取消回复

文章目录