支持向量机（Support Vector Machine，SVM）是 Vapnik 等人在 1995 年完善的经典监督学习算法，可广泛应用于分类与回归任务。凭借严谨的数学理论支撑与出色的泛化能力，它在深度学习兴起之前长期是文本分类、图像识别等领域的主流模型。即便如今深度学习成为行业主流，在小样本、高维度的数据场景下，SVM 仍能展现稳定可靠的性能，具备极高的实用价值，是机器学习入门阶段的核心基础算法。

1. 算法初探

支持向量机的预测过程，是先通过一个线性函数计算出一个标量值，这个值表示模型对该样本所属类别的置信程度，然后根据符号决定预测类别。

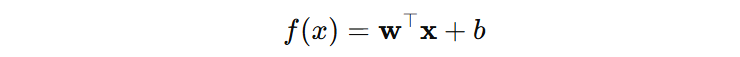
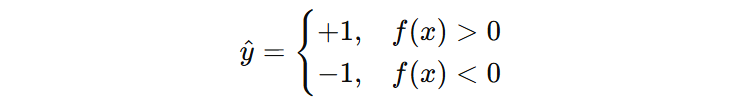
例如：经过训练我们得到两个参数分别为：\(w=(2,−1)，b=−1\)，即：\(f(x)=2x_{1}−x_{2}−1\)。接下来，需要计算新样本 \(x=(2,1)\) 的类别，代入函数中，得到 \(f(x)=2 \gt 0\)，最终新样本输出类别是 \(+1\) 类别。

这里有两个注意点：

支持向量机类别标签为 +1 和 -1；
支持向量机默认不提供概率解释。

在支持向量机中，模型的参数 \(w\) 和 \(b\) 是通过训练样本计算得到的。这里有一个关键要点：只有训练集中的一部分样本会对最终的决策函数产生影响，这些样本就是我们所说的支持向量，这也是支持向量机名字的由来。

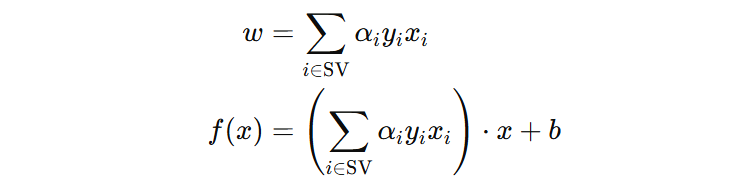
所以，我们可以简单理解为：支持向量机的训练过程，本质上就是在寻找这些关键的支持向量。

2. 优化目标

支持向量机之所以只依靠少数支持向量，就能得到泛化能力很强的模型，核心要从它的优化思路说起。支持向量机是这么想的：

假设训练阶段模型学到的正类样本是 \(x=(2.1,3.5,1.8)\)，但在实际预测时，受噪声、测量误差影响，输入可能变成 \(x=(2.08,3.52,1.81)\) 这类轻微扰动后的向量，普通模型就可能把它误判为负类。支持向量机正是为了解决这个问题：让模型的输入存在微小干扰时，依然能稳定、正确地分类。

简单来说：支持向量机的核心目标，就是最大化模型对输入的抗扰动能力，从根源上提升模型的泛化能力。

2.1 扰动分析

既然支持向量机的核心目标是提升模型的抗扰动能力，我们先分析下当输入中添加扰动的时候，如何进行优化。假设：样本可能受到小扰动 \(\delta_{i}\)，上限为 \(\epsilon_{i}\)，注意：每个样本都有一个扰动。

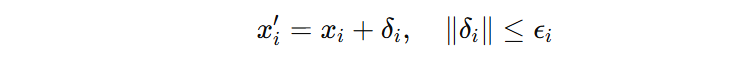
当一个样本分类正确时，我们可以用下面的公式表示：

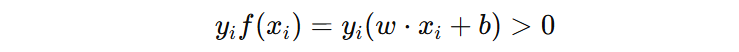
当添加扰动后，依然分类正确时，用下面的公式表示：

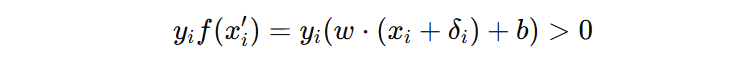
展开后可得：

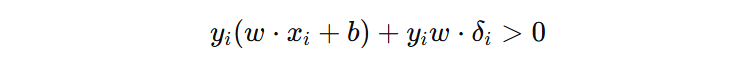
\(y_{i}w\delta_{i}\) 是扰动带来的负面影响，当该项足够小的时候，就可能会改变分类结果。接下来，我们分析下最坏情况下的扰动怎么表示（即：该项最小能有多小）：

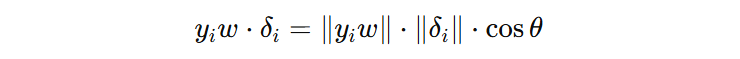
我们发现，当 \(\theta\) 为 π 时，\(\delta_{i}\) 达到扰动的上限。

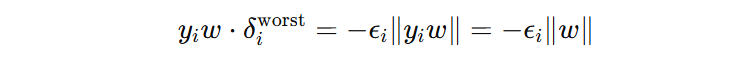
其中，\(||y_{i}w||\) = \( |y_{i}| ||w||\) = \(||w||\)，这就是引入的最坏情况下的扰动，把最坏扰动代回原始条件：

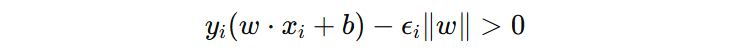
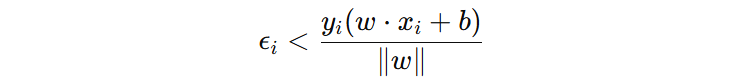
此时不难发现：样本能承受的最大扰动上限，恰好等于该样本到超平面的几何距离。也就是说，距离超平面越远的样本，抗扰动能力越强；反之则越容易因微小扰动导致分类错误。

为了保证所有的样本都具有非常好的抗扰动能力，我们在选择 \(w、b\) 时，要保证距离超频面最近的样本，到超平面的几个间隔尽可能的大。所以，支持向量机的优化目标可表示为：

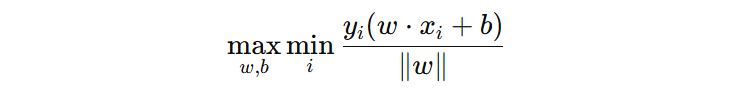
该式称为最大化最小几何间隔，含义是：在所有样本中找到到超平面距离最小的样本，并通过调整 \(w\) 和 \(b\)，使这个最小距离最大化。

2.2 目标简化

假设所有样本到超平面的最小几何距离为 \(\gamma_{min}\)：

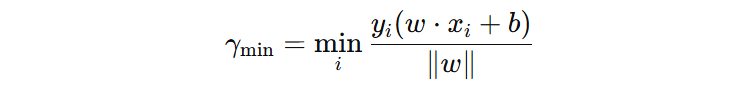
分子：\(y_{i}(w·x_{i}+b)\) 叫做 \(x_{i}\) 到超平面的函数间隔。
分母：当确定超平面的时候，分母就是常数，不同的样本到超平面的距离是由分子决定的，所以公式可以转换为下面的形式：

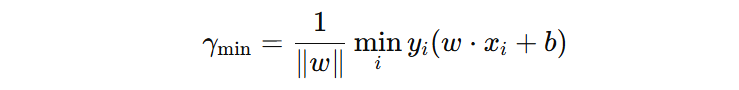
接下来，我们继续简化优化目标，这里有两个重要点。

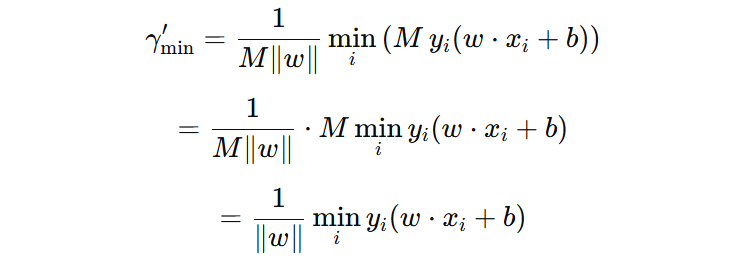
1️⃣ 当我们任意缩放 \(w、b\) 时，样本到超平面的几何间隔不变。

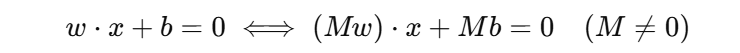
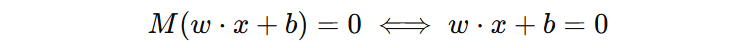
2️⃣ 当我们任意缩放 \(w、b\) 时，超平面的位置不变。

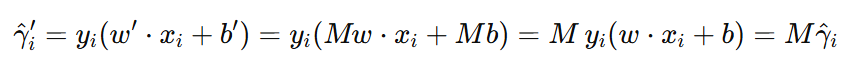
3️⃣ 缩放 \(w、b\) M 倍，函数间隔的大小也会缩放 M 倍。

重点：\((w, b)\)、\((3w, 3b)\) … \((Mw, Mb)\) 都可以表示我们得到的最优超平面，但是，但是同一个超平面对应着无数组的参数，这种现象称为尺度不确定性。

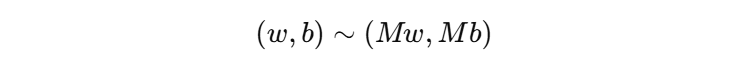
为了解决这个尺度不确定性的问题，我们需要进行一个尺度规范化的操作。具体做法是，原来没有进行 \((w, b)\) 尺度约束时，\(y_{i}(w·x_{i}+b)\) 可以是任意的值，本身没有固定数值。为了避免这种随意性，我们干脆选定一个标准，把它规定为 1，这样一来，参数 \((w, b)\) 的尺度也相当于间接确定了。

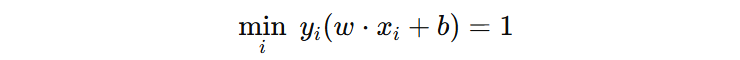
注意：

这里选择 1，也可以是 2 … 选择1仅仅是为了使得目标函数更加简单。
我们只是把距离超平面最近的样本的函数间隔固定为1。

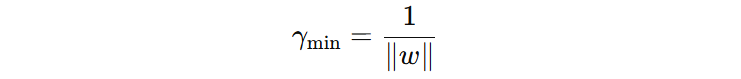
注意：\(y_{i}(w·x_{i}+b)\) 现在最小值是 1，所以，优化目标公式可以表示为：

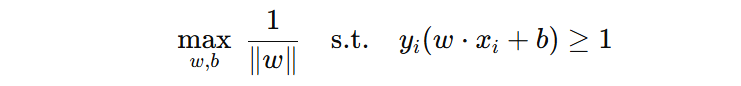
我们再仔细理解下这个约束条件，它不仅要求分对，还要求分得有安全距离。它优化的不是平均表现，而是提升最危险样本的置信度，从而让模型整体更加稳健。

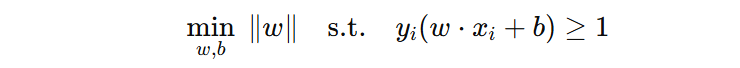
为了便于求解，通常将目标函数写成：

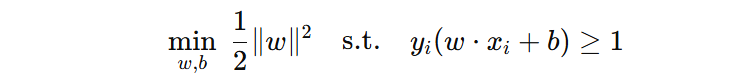
目标函数的含义是：在所有样本均被正确分类、满足分类约束的前提下，最大化距离超平面最近样本的几何间隔，从而获得泛化能力更好的线性分类模型。

3. 约束松绑

目标函数要求所有样本都能够正确分类，并且函数间隔大于等于1，但现实数据中往往存在噪声、异常点，导致部分样本无法满足 \( y_{i}(w·x_{i} + b) \ge 1 \) 的严格约束，导致优化问题无解，算法根本无法运行。

支持向量机为了适应实际场景，对约束条件进行了松绑，允许部分样本违反约束条件，即：允许部分样本函数间隔违例。

这里要注意一个重要的点，函数间隔违例的程度大，并不能说明模型泛化能力不好（允许噪声、异常带来的代价，换来更稳健的分类超平面），函数间隔违例的程度小，也不能说明模型的泛化能力就一定好（为了减少违例程度，扭曲分类超平面）。注意：函数间隔违例的程度，既包含每个样本违规的程度，也包含违规的样本数量。

所以，在允许函数间隔违例场景下，我们需要的目标函数，要能够让我们去平衡函数间隔违例的程度和几何间隔，从而获得当前问题场景下泛化能力更好的模型。

3.1 松弛变量

软约束支持向量机引入一个非负松弛变量 \(\xi\)，记录每个样本函数间隔违例的程度。比如：\(\xi = 0.3\)，表示我们希望该样本函数间隔至少为 1，但实际输出只有 0.7，因此差了 0.3。

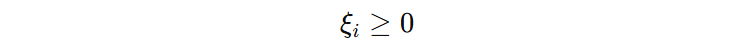
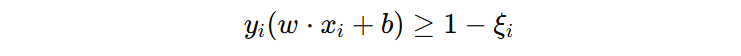
此时，原始的约束条件具有一定的弹性、灵活性，样本就不会违背约束了，这就是软约束的支持向量机。接下来，我们将函数间隔违例程度引入到目标函数中，便于我们去平衡函数间隔违例的程度和几何间隔。

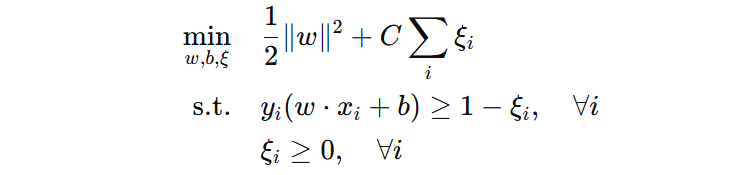
此时，优化目标就不再单纯追求最大的几何间隔，而是要综合考虑几何间隔和函数间隔违例代价，使得两者达到一个平衡，目标函数最小，得到理论上最优的模型。但是这里需要注意，这个理论最优不一定是泛化能力最好的模型。

为了调节几何间隔与违例代价之间的相对重要性，引入了超参数 \(C\)。不同的 \(C\) 实际上对应着不同的优化侧重方向，也就对应着不同的理论最优超平面。

\(C\) 为1 ：两项代价权重相等，模型在间隔大小和违例代价之间折中选择最优超平面；
\(C\) 越大：违例代价惩罚越严格，模型更倾向于让训练样本满足约束，增加过拟合风险；
\(C\) 越小：违例代价惩罚越宽松，模型允许更多样本违反约束，可能提升稳健性，但过小也可能导致欠拟合。

超参数 C 并不存在通用的理想取值，其最优选择依赖于训练数据的分布特征和噪声水平。因此，通常通过交叉验证配合网格搜索，从候选 C 值中选择在验证集上泛化表现最好的参数。

3.2 问题转换

软约束支持向量机的目标函数是带不等式约束的优化问题，直接求解难度较大。通过拉格朗日乘子法，可将其转化为无约束优化问题，为后续求解奠定基础。接下来，我们遵循通用规范流程，将带约束的目标函数转换为一个拉格朗日函数。

1️⃣ 给第一个约束加乘子 \(\alpha_{i} \ge 0\)：

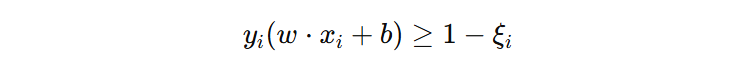
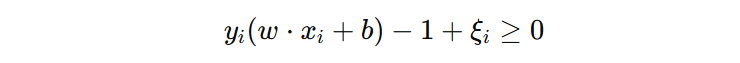
2️⃣ 给第二个约束加乘子 \(\mu{i} \ge 0\)

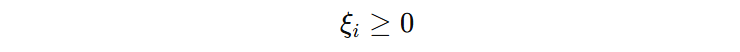
3️⃣ 我们将目标和约束合成一个拉格朗日函数，把带约束的最小化问题，变成一个无约束的问题:

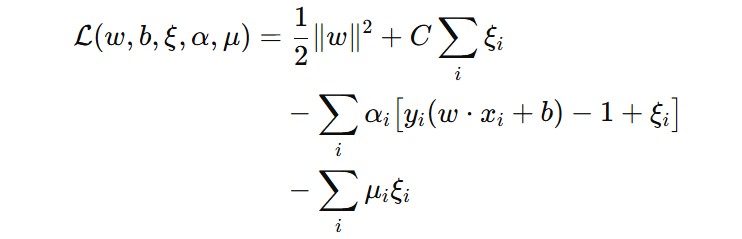
这里需要注意，原来优化的是 min 问题，现在则变成一个 min–max 问题？

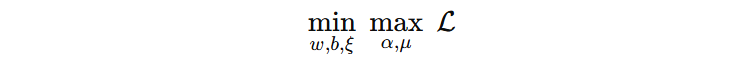
在拉格朗日函数中，前两项对应的是原始优化目标，后两项对应的是约束条件。如果在引入拉格朗日函数之后，仍然把整个问题当作一个单纯的最小化问题来处理，就会出现一个严重的问题：为了使拉格朗日函数的值尽可能小，算法并不一定需要真正优化前两项的目标函数，而是可以通过操纵约束项来不断降低整体数值。

具体来说，当约束条件被满足时，对应的约束项是小于等于零的，同时拉格朗日乘子 α 又被限制为非负。在这种情况下，只要不断增大 α，就可以让拉格朗日函数的值持续下降，从而把“满足约束”错误地当成了一种可以用来降低目标函数的手段。

这显然违背了约束的初衷，因为约束的作用并不是参与优化打分，而只是用来区分解是否合法。正因为如此，约束条件不能被当作一个可以被无限优化的项，而必须被冻结在一个恰当的状态。因此，在拉格朗日函数中对拉格朗日乘子引入最大化（max）：当约束被满足时，最大化会使约束项达到其允许的最大值，从而不再对整体目标产生影响；当约束被违反时，最大化会将拉格朗日函数的值推向无穷大，模型越想找到一个超平面，所有样本都满足约束。

这样，整体优化过程才变成：先通过 max 阻止约束项被当作优化手段，再在满足约束的解集合中，搜索 \(w、b、\xi\)，从而使原始的优化目标得以正确实现。

3.3 对偶问题

原问题想直接找最优超平面，但是需要先对 \(\alpha、\mu\) 求最大，再对 \(w、b、\xi\) 求最小，这样的的双层嵌套优化问题求解太难了。

为了更容易求解，我们不直接找到最优超平面，而是先找每个样本对超平面的贡献（拉格朗日系数），然后再间接得到最优超平面。这种思路也叫做原问题的对偶形式、对偶问题，问题本身没有变，只是换了一种求解思路。

对偶问题的核心步骤是：

对 \(w、b、\xi\) 求偏导，并让其等于 0（这就是 KKT 的一部分）。
将 \(w、b、\xi\) 表示成关于 \(\alpha_{i}\) 的函数。
代回拉格朗日函数，得到只关于 \(\alpha\) 的对偶问题。

KKT 条件的作用：给出原问题最优解与拉格朗日乘子之间必须满足的关系，用来将原问题变量 \(w、b、\xi\) 表示为拉格朗日乘子 \(\alpha\) 的函数，从而构建对偶问题。

对 \(w\) 求导并令其为 0：

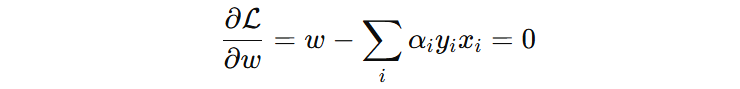
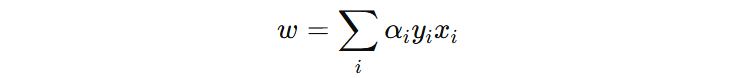
对 \(b\) 求导并令其为 0：

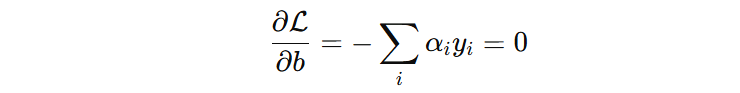
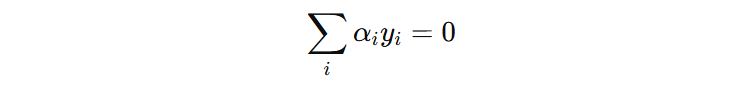
对 \(\xi\) 求导并令其为 0：

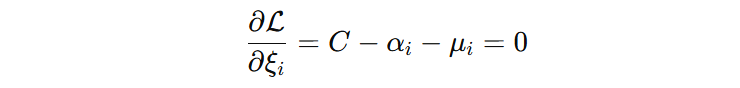
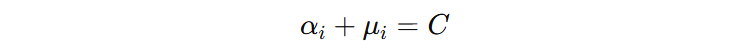
由于 \(\mu_{i} \ge 0\)，所以：

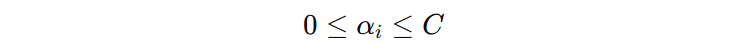
这里再次碰到 C 了，我们再加深对 C 超参数的理解。我们前面在讲解 min-max 问题时，提到当函数间隔违例的时候，算法会无上限的放大这些代价，使得模型要尽可能的减少函数间隔违例。这种不加控制的惩罚方式，很容易使得模型过拟合。通过 C 参数控制了惩罚上限，间接影响了分类超平面。

接下来，我们将上述公式代回拉格朗日函数，消去 \(w、b、\xi\)，得到只与 \(\alpha\) 有关的问题：

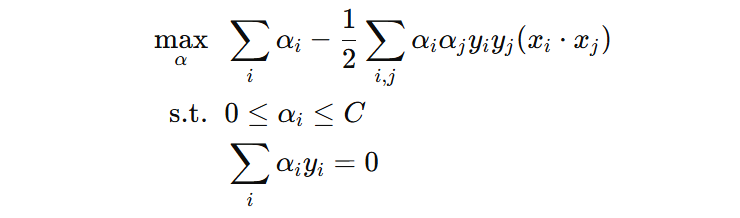
我们需要结合训练样本，求解出每个样本对应的 \(\alpha_{i}\)，就可以得到超平面的关键参数 \(w\) 和 \(b\) 。虽然从理论上当前问题存在最优解，但需要同时决定每一个样本对应的参数，数量庞大且相互牵制。因此在实际中，求解的难点不在于是否有解，而在于如何高效地将其计算出来，通常采用序列最小优化（SMO）等算法，通过每次优化两个拉格朗日乘子，逐步迭代得到最优解。

求解出的 \(\alpha\) 有以下几种情况：

\(\alpha = 0\)，样本分类正确，没有违反约束， \(y_{i}(w·x_{i}+b) > 1\)；
\( 0 \lt \alpha \lt C\)，样本分类正确，在函数间隔边界上 \(y_{i}(w·x_{i}+b) = 1\)；
\(\alpha = C\)，违反约束条件（可能分类错误，也可能分类正确）\(y_{i}(w·x_{i}+b) < 1\)

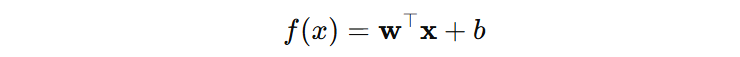
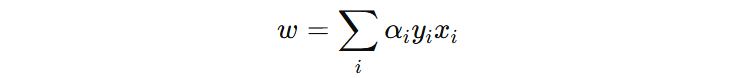
决策函数 \(w、b\) 是由 \(\alpha \gt 0\) 的样本集合决定，这些样本也叫支持样本（向量），这也是支持向量机名称的由来。决策函数一般也写成如下形式：

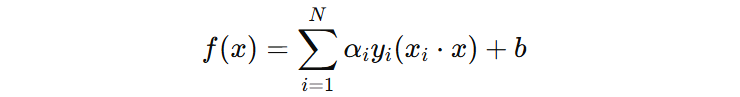
\(xi_{i}⋅x\) 本质上是在问：新样本 x 和第 i 个训练样本像不像
\(y_{i}\) 规定这个样本是支持正类还是支持负类
\(\alpha_{i}\) 第 i 个样本在最终决策中有多重要

新样本 \(x\) 来了，让训练集中重要的样本逐个出来，看看它们和 \(x_{i}\) 有多像，然后按它们的立场和话语权加权投票。

4. 核函数

软约束支持向量机仍局限于线性分类（线性可分、近似线性可分）场景。当数据是非线性分布（如内外环、螺旋形分布）时，即便允许样本违反约束，在原始特征空间中也无法找到合适的分类超平面。

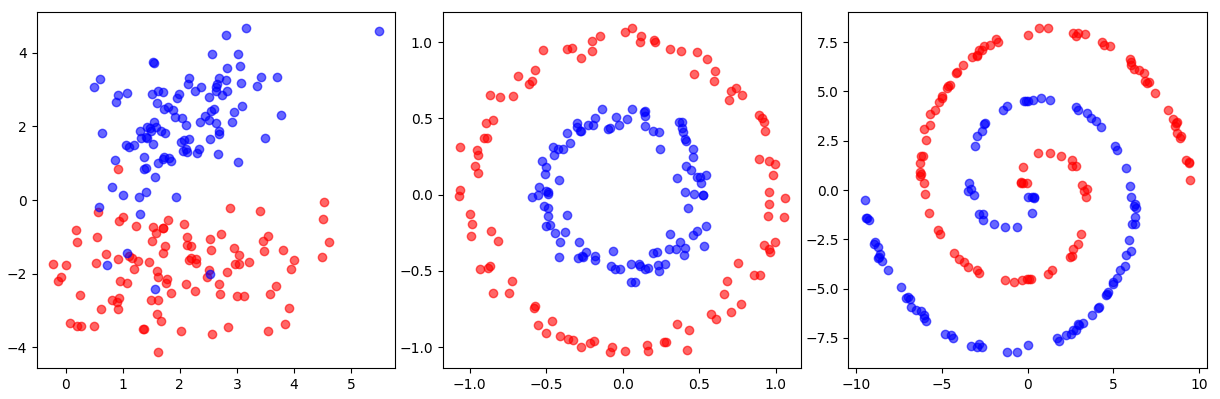
那怎么解决呢？思路并不是再放宽约束，而是换一个看问题的空间。在原始特征空间里，数据是非线性缠绕的，看起来怎么都画不出一条合情合理的直线。但如果把数据通过某种非线性变换映射到一个更高维的空间，原本弯曲、交错的结构，在新空间中变得线性可分。

这里有个理解的点：支持向量机在高维空间中是仍然是最大化间隔，寻找线性超平面，但是从原空间的角度来看，这个超平面就变成非线性的。

那么，我们就把数据映射到更高维空间，在更高维的空间去寻找最大间隔的线性超平面。但直接进行高维映射存在 2 个问题：

计算复杂度极高：高维空间的特征维度可能非常高，甚至无穷维。
映射函数未知：难以找到合适的实现有效映射。

核函数正是在这里登场的，它让我们无需真的进行高维映射（核技巧），只需在原空间中计算样本之间的相似度，就等价地完成了在高维空间中训练 SVM。

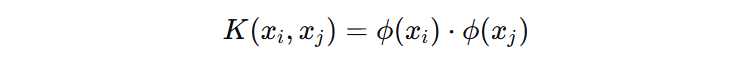
\(\phi(x)\) 表示映射函数，用于把原来的数据 \(x\) 映射到高维空间。

核函数支持向量的决策函数如下：

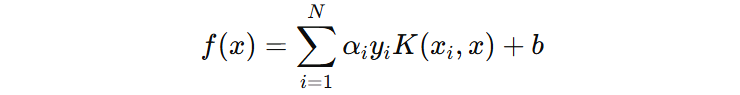
常见的核函数有：

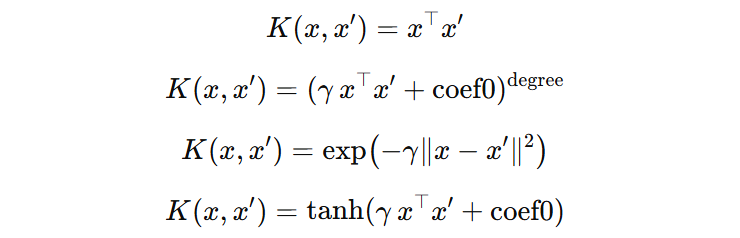
5. 打完收工

决策函数：通过决策函数 \(f(x)=sign(\sum_{i} \alpha_i y_i K(x_i, x) + b)\) 输出标量，依据符号判定类别 +1 或 -1。支持向量机决策函数是由部分 \(\alpha > 0\) 的样本决定，这些样本叫做支持向量。

间隔最大化思想：SVM 的本质是寻找最稳健的分类超平面，让两类样本到超平面的最小几何间隔最大化。这一思想的核心逻辑是：样本到超平面的距离直接等价于其抗扰动能力，几何间隔越大，样本受噪声、小扰动影响时分类结果越稳定，从而保障模型泛化能力。

有限样本最优思想：针对小样本、高维数据场景设计，不追求对训练数据的绝对拟合，而是通过数学推导实现有限样本下的最优分类边界，这也是其在深度学习兴起后仍能立足的核心原因。

约束平衡思想：承认现实数据的噪声与异常点，通过 “硬约束→软约束” 的松弛与惩罚机制，在 “分类准确性” 和 “模型稳健性” 之间寻找平衡，避免极端情况（完全不允许分错导致过拟合，或过度宽松导致欠拟合）。

超参数 C 影响：C 越小，惩罚越宽松，泛化能力可能提升。C 越大，惩罚越严格，模型倾向于完全正确分类，可能过拟合，需通过网格搜索优化。

核技巧思想：面对非线性数据，通过将低维非线性数据映射到高维线性可分空间，再通过核函数避免高维计算的爆炸式复杂度，用原空间样本相似度等价替代高维空间点积，实现高效非线性分类。

多分类 SVM：SVM 本质是二分类，需要 one-vs-rest 或 one-vs-one 扩展。

支持向量机（Support Vector Machine）