梯度提升树(Gradient Boosting Decision Tree,简称 GBDT)由 Friedman 提出,是集成学习领域的经典算法。
- 在深度学习尚未兴起的年代,GBDT 几乎是结构化数据建模的首选方案,在很多领域都表现出稳定出色的性能。
- 即便在今天,许多互联网公司的核心业务仍然高度依赖 GBDT 相关模型(如 XGBoost、LightGBM)。
因此,GBDT 依旧具有极高的学习价值,是每一位数据科学从业者都应深入掌握的重要算法。
1. 基本原理

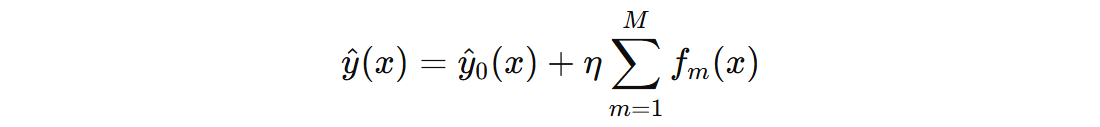
GBDT 由一个初始策略 + 多个决策树组成,每个决策树叫做弱决策树或者弱学习器,整体叫做强学习器。
1.1 预测过程
- 初始输出:给出一个固定常数作为预测起点(训练后确定)
- 修正输出:使用训练好的每棵树得到对应的预测修正值(每个输出需要乘以学习率)
- 累加输出:将初始输出与所有树的输出累加得到最终预测
如果没有学习率,单棵树的输出可能过大,一旦这棵树受到噪声影响,其错误也会影响到到最终预测,导致整体结果偏差很大。加入学习率后,可以控制每棵树对最终结果的影响,即使当前树有偏差,也不会让最终预测产生过大的错误。
学习率让削弱了单棵树的纠错力度,却显著提升了模型的稳定性与鲁棒性。虽然需要更多的树(例如原本 10 棵树能完成的任务,学习率为 0.1 时可能需要 100 棵树),但这种以稳取准的策略能有效抵抗噪声和异常样本的干扰。
1.2 训练过程
模型先由初始预测(基准值)开始,之后每棵树依次拟合前一阶段的预测差距,逐步修正已有模型的偏差,直到达到预设的树数量或模型性能不再提升时停止训练。
假设:两个样本,真实值分别是 86 和 98,学习率 0.1,我们模拟下训练过程:
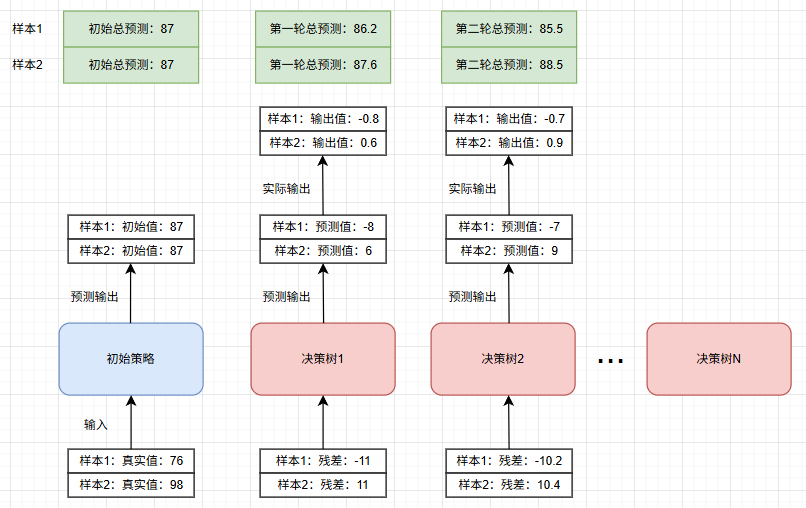
模型训练的起点是初始预测(基准值),该值并非随机设定,而是由选定的损失函数推导得出。其核心目的是为后续迭代优化提供一个基础参照,尽可能降低初始偏差。例如在平方损失函数场景下,初始预测值会直接取所有样本标签的均值 , 这一选择本质是最小化平方损失的最优解,能让模型从一个相对合理的基准状态启动训练。
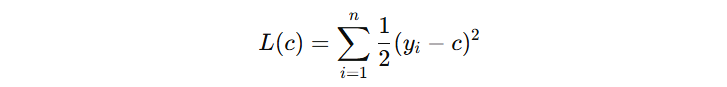
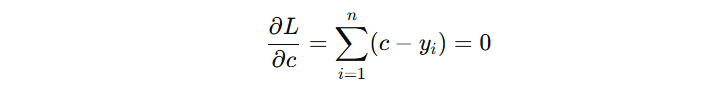
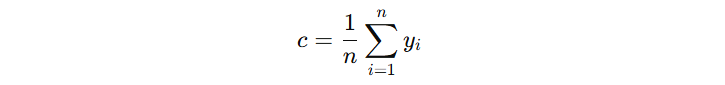
每一棵新树训练时拟合的残差,并不是简单真实值和预测值的差值,而是损失函数对预测值的负梯度,数学上表示损失函数最小化的优化方向。
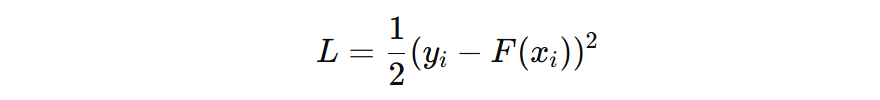
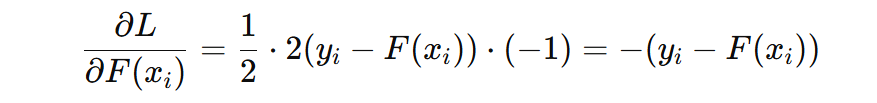

比如:第一棵树拟合的 -11、11 就是损失函数对初始预测的负梯度
- -11 表示第一个样本需要向着负方向再减少11,才能达到目标值
- 11 表示第一个样本需要向着正方向再增加11,才能达到目标值
我们总结几点:
- 训练模式:模型以串行方式训练多棵决策树,即只有当前一棵树训练完成后,下一棵树才能开始训练
- 拟合目标:每棵新树都不是直接去拟合真实值,而是拟合前序模型的负梯度。
- 核心逻辑:模型通过逐棵树不断修正预测误差,使整体预测逐步逼近真实目标。
- 需要注意:随着树的增多,模型会越来越贴合训练数据,可能会导致过拟合。
注意:无论 GBDT 用于回归还是分类,由于拟合目标都是负梯度(连续值),所以弱学习器都是回归决策树。
2. 公式推导
在 GBDT 的训练过程中,每棵新树的核心任务是拟合前一轮模型的负梯度,以此逐步修正预测误差。要完成这棵树的训练,需明确两个关键问题:
- 树的分裂规则:如何计算特征分裂时的增益,从而选择最优分裂点?
- 叶子节点输出:分裂结束后,每个叶子节点应输出什么值,才能最大化误差修正效果?
先看第一个问题:GBDT 训练每棵树的核心目标是精准拟合负梯度、降低整体误差,不需要考虑树的复杂度。因此,选择能直接反映拟合效果提升的分裂增益指标即可,常用的有平方误差(squared_error)或弗里德曼均方误差(friedman_mse),scikit-learn 等工具默认采用 friedman_mse,这一步无需额外推导公式,直接选用成熟指标即可。
再看第二个问题:叶子节点输出值的确定,这是 GBDT 训练的关键难点,且结果与损失函数直接相关,不能一概而论:
- 若使用平方损失函数,情况较简单,叶子节点的最优输出值,等价于该节点内所有样本负梯度的均值。
- 若使用非平方损失函数(如 log loss),则无法直接用负梯度均值作为最优输出。此时必须通过最小化该叶子节点内所有样本的累计损失来求解最优值 。
- 这一步是需要推导的。
简单来说:分裂增益的选择是 “选工具”,优先挑能高效拟合负梯度的成熟方法。而叶子节点输出是 “定结果”,必须贴合损失函数的特性,平方损失有简洁结论,非平方损失则需通过损失最小化单独求解。
2.1 目标函数
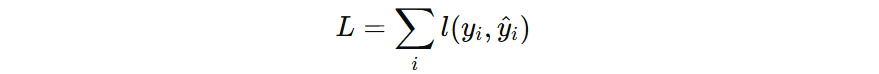
公式表示,所有训练样本的损失总和。
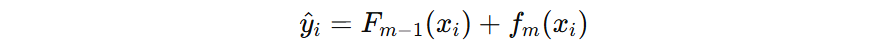
公式表示,模型的预测结果 \( \hat{y} \) 等于 \( m-1 \) 树的输出结果 + 当前树 \(f_{m}\)的输出结果。
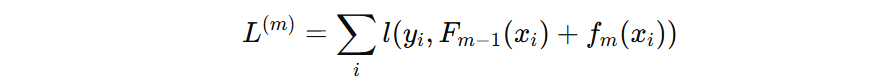
我们通过一个例子来理解损失函数:假设目标值为 100、初始预测值为 20,此时初始损失为 6400。后续每新增一棵树,都会通过拟合负梯度的方式,最终实现损失函数的最小化。
| 轮次 | 拟合残差 | 实际输出 | 总预测更新 | 当前损失 | 损失下降幅度 | 说明 |
|---|---|---|---|---|---|---|
| 第 1 棵树 | 80 | 30 | 50 | 2500 | -3900 | 损失大幅下降 |
| 第 2 棵树 | 50 | 10 | 60 | 1600 | -900 | 损失持续下降 |
| 第 3 棵树 | 40 | 30 | 90 | 100 | -1500 | 损失进一步下降 |
后续树循环拟合剩余残差,总预测逐步逼近目标值,总损失持续向 0 收敛。
优化目标:确定每棵新树 \(f_{m}\) 如何输出(叶子节点输出值),能够最小化损失函数。
2.2 泰勒展开
由于 \( l \) 可能是任意复杂的非线性函数,并且我们要优化的 \( f_{m}(x) \) 是整个损失函数内部的一部分,直接对 \( f_{m}(x) \) 优化不现实。所以,我们使用泰勒二阶展开将损失函数近似成一个关于 \( f_{m}(x) \) 的二次函数,这样就能继续优化 \(f_{m}\)。
泰勒二阶展开是利用损失函数在某个已知点、以及其一阶导和二阶导信息,近似表示加入新树后损失表示。泰勒二阶展开公式如下:
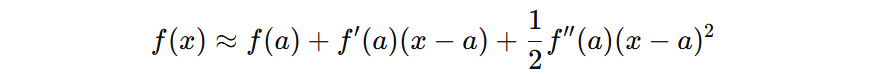
对应到当前的场景:
- \(a\) 表示截止到 m-1 树时的模型输出值
- \(x\) 表示截止到 m 树时的模型输出值
- \(x-a\) 表示第 m 棵树带来的模型输出增量
- \(f(a)\) 表示截止到第 m-1 棵树时,模型的损失函数值
- \(f^{\prime}(a)\) 表示损失函数在 a 处对模型输出的一阶导数
- \(f^{\prime\prime}(a)\) 损失函数在 a 处对模型输出的二阶导数
我们对损失函数在已知点 \( m-1 \) 位置进行泰勒二阶展开:
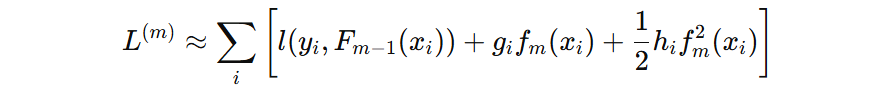
- \( g_{i} \) 表示第 i 样本在损失函数上的一阶导值
- \( h_{i} \) 表示第 i 样本在损失函数上的二阶导值
- \( f_{m}(x_{i}) \) 表示样本 \( x_{i} \)在第 m 棵树的输出值
\( l(y_i, F_{m-1}(x_i)) \) 表示还没有加入新树时的损失,是常数项,可以去掉,我们就得到了一个关于 \( f_{m}(x_{i}) \) 的公式:
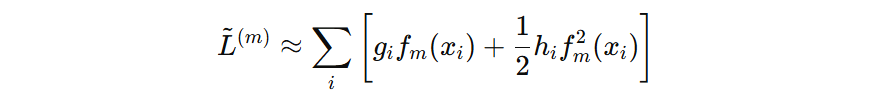
我们通过最小化这个目标函数,来找到第 m 棵树的最优输出值(叶子节点的输出值)。
我们要推导叶子结点最优输出值,将上面公式转为从叶子节点角度表示的目标函数。为了简便,我们用 \( \gamma_{j} \) 表示第 \(j\) 个叶子节点的输出值。
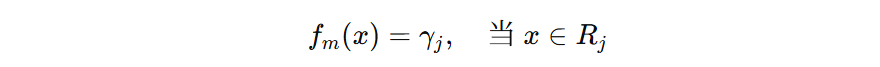
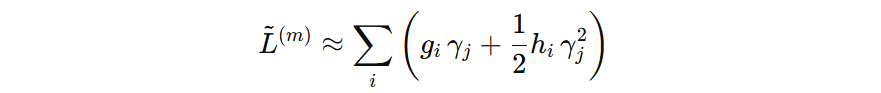
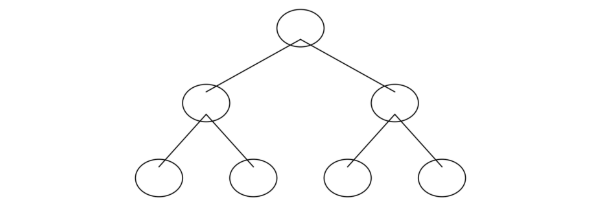
每个样本的输出值对应某个叶子节点的值,所以我们可以以叶子节点为单位计算每个样本的输出值、一阶导、二阶导,那么得到如下公式:
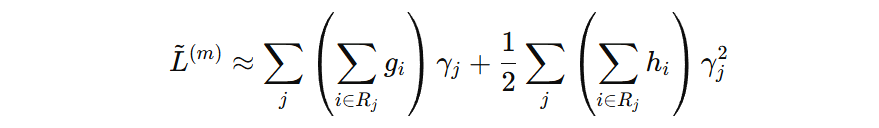
我们将公式再简化一些:
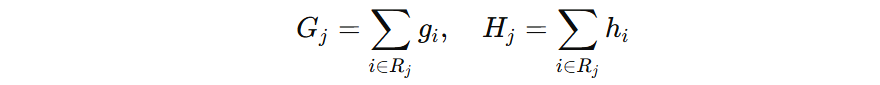
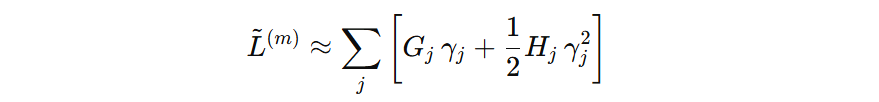
2.3 最优输出
叶子结点如何输出,目标函数最小?我们只需要对 \( \gamma \) 求导,并令导数等于 0。
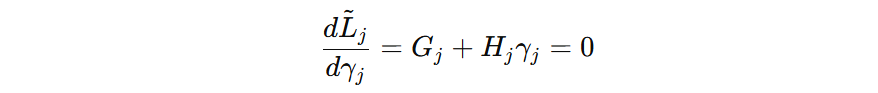
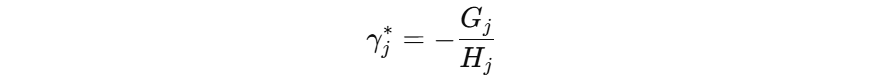
假设我们使用 log loss、square loss 损失函数,那么叶子节点的输出值公式为:
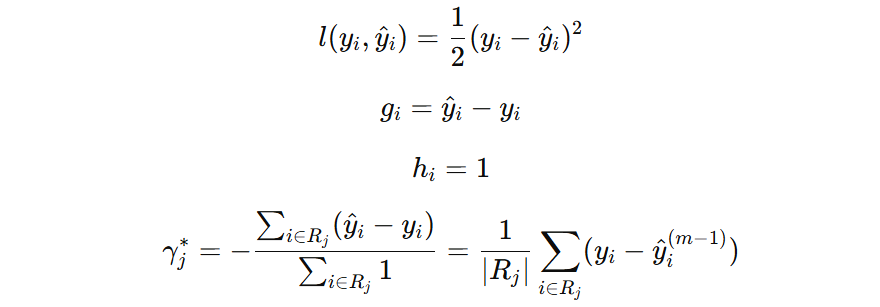
注意:\( (y_i – \hat{y}_i^{(m-1)}) \) 表示本轮样本的负梯度。
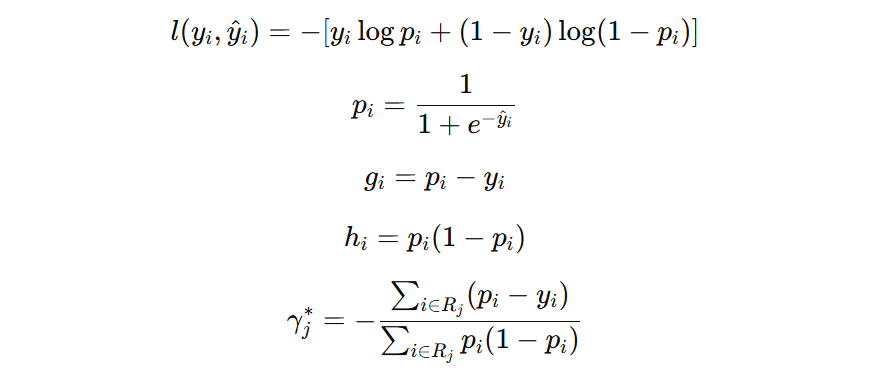
3. 计算案例
| 序号 | 特征 1 | 特征 2 | 特征 3 | 标签 |
|---|---|---|---|---|
| 1 | -0.587231 | -1.971718 | -1.057711 | 0 |
| 2 | 1.068339 | -0.970073 | 0.208864 | 1 |
| 3 | -1.140215 | -0.838792 | 0.822545 | 0 |
| 4 | -0.077445 | -1.599711 | -1.220844 | 0 |
| 5 | 1.727259 | -1.185827 | -1.959670 | 1 |
| 6 | -2.895397 | 1.976862 | 0.196861 | 0 |
| 7 | -1.962874 | -0.992251 | -1.328186 | 0 |
| 8 | 1.899693 | 0.834445 | 0.171368 | 1 |
| 9 | -0.720634 | -0.960593 | -0.013497 | 0 |
| 10 | -1.715464 | 2.173706 | 0.738467 | 0 |
3.1 初始预测
GBDT 的初始模型 \( \hat{y}_{0}(x) \) 为每个样本提供一个基础的预测值,后续每棵子树都在此基础上,通过拟合当前残差(或负梯度)来进一步优化预测结果。
注意:初始模型 \( \hat{y}_{0}(x) \) 的输出通常是一个常数(即对所有样本预测同一个值)
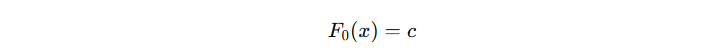
那么,这个初始模型的输出值 c 怎么确定?对于经典的二分类问题,我们一般使用的 log loss 损失函数,其公式如下:
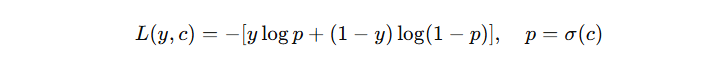
对于初始模型来讲,看看 c 输出什么时,损失函数最小。我们对 c 求导,设导数为 0:
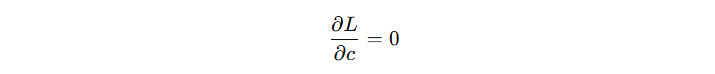
得到初始输出计算公式(省略中间化简过程):
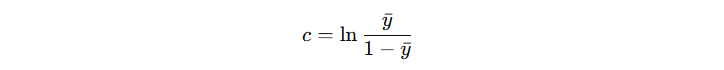

由此可得,初始模型的输出结果为:
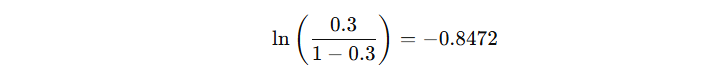
3.2 拟合残差
GBDT 分类模型默认使用二分类损失函数 log loss,其负梯度计算公式为:
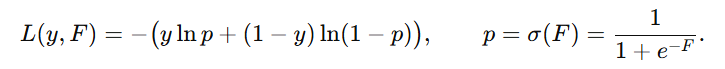
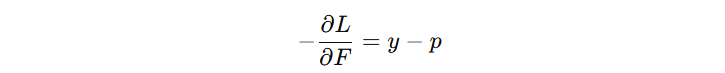
- \( p \) :预测概率
- \( y \) :真实标签(0 或 1)
| 序号 | 真实标签 | 初始分数 | 预测概率 | 负梯度 |
|---|---|---|---|---|
| 1 | 0 | -0.8472 | 0.3 | -0.3 |
| 2 | 1 | -0.8472 | 0.3 | 0.7 |
| 3 | 0 | -0.8472 | 0.3 | -0.3 |
| 4 | 0 | -0.8472 | 0.3 | -0.3 |
| 5 | 1 | -0.8472 | 0.3 | 0.7 |
| 6 | 0 | -0.8472 | 0.3 | -0.3 |
| 7 | 0 | -0.8472 | 0.3 | -0.3 |
| 8 | 1 | -0.8472 | 0.3 | 0.7 |
| 9 | 0 | -0.8472 | 0.3 | -0.3 |
| 10 | 0 | -0.8472 | 0.3 | -0.3 |
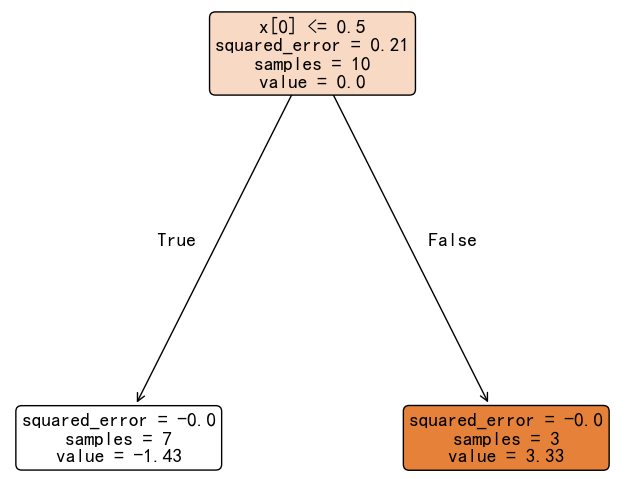
上图中,预测概率是 sigmoid(输出分数) 得到,在构建第一个决策树时,模型的输出就是初始分数。接下来,将负梯度作为拟合目标,训练第一个弱决策树:
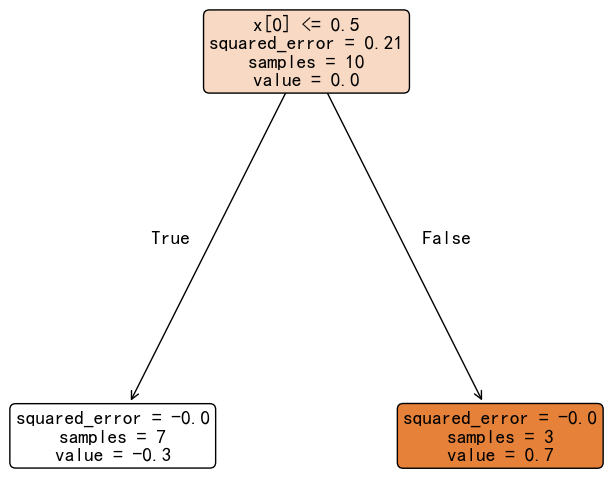
决策树叶子节点输出值默认为该节点上样本目标值的均值。但实际上,叶子节点最终输出值需要根据损失函数进行修正。对于 log loss,叶子节点输出值的修正公式如下:
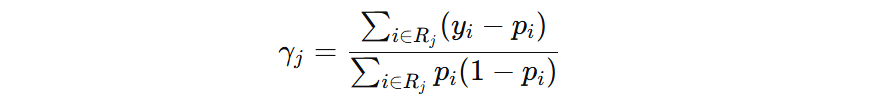
- 左叶子节点(7 个 0 样本):-0.3 / (0.3 * 0.7) = -1.43
- 右叶子节点(3 个 1 样本):0.7 / (0.3 * 0.7) = 3.33
修正之后的决策树为:
按照前面的思路继续构建第二棵子决策树(学习率为 0.1):
| 序号 | 标签 | 预测分数 | 预测概率 | 负梯度 |
|---|---|---|---|---|
| 1 | 0 | -0.99016 | 0.27 | -0.27 |
| 2 | 1 | -0.51396 | 0.37 | 0.63 |
| 3 | 0 | -0.99016 | 0.27 | -0.27 |
| 4 | 0 | -0.99016 | 0.27 | -0.27 |
| 5 | 1 | -0.51396 | 0.37 | 0.63 |
| 6 | 0 | -0.99016 | 0.27 | -0.27 |
| 7 | 0 | -0.99016 | 0.27 | -0.27 |
| 8 | 1 | -0.51396 | 0.37 | 0.63 |
| 9 | 0 | -0.99016 | 0.27 | -0.27 |
| 10 | 0 | -0.99016 | 0.27 | -0.27 |
预测分数 = 初始分数 + 学习率 * 第一棵树输出分数。以第一个样本为例,计算负梯度:
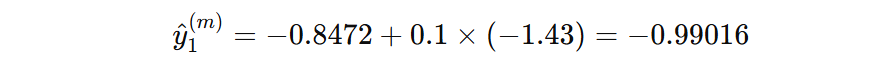
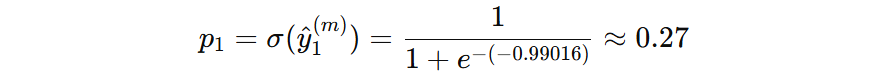
接下来,训练新树去拟合本轮负梯度,然后再修正叶子节点输出,重复此过程。




 冀公网安备13050302001966号
冀公网安备13050302001966号