AdaBoost(Adaptive Boosting,自适应提升)算法由 Yoav Freund 和 Robert Schapire 于 1995 年提出,是一种能自动找出薄弱环节并不断改进的集体学习方法,是机器学习历史上具有里程碑意义的算法。它首次在理论上证明:即使是性能较弱的模型,只要经过合理的组合,也能形成一个强大的分类器。凭借简单而高效的设计,它在图像识别、医学诊断、金融风控等多个领域得到广泛应用。
传统 AdaBoost 用于二分类,Scikit-Learn 中实现的是其多分类扩展版本 SAMME(Stagewise Additive Modeling using a Multi-class Exponential loss)。
Paper:https://link.intlpress.com/JDetail/1806634576447516674
1. 基本原理
1.1 预测过程
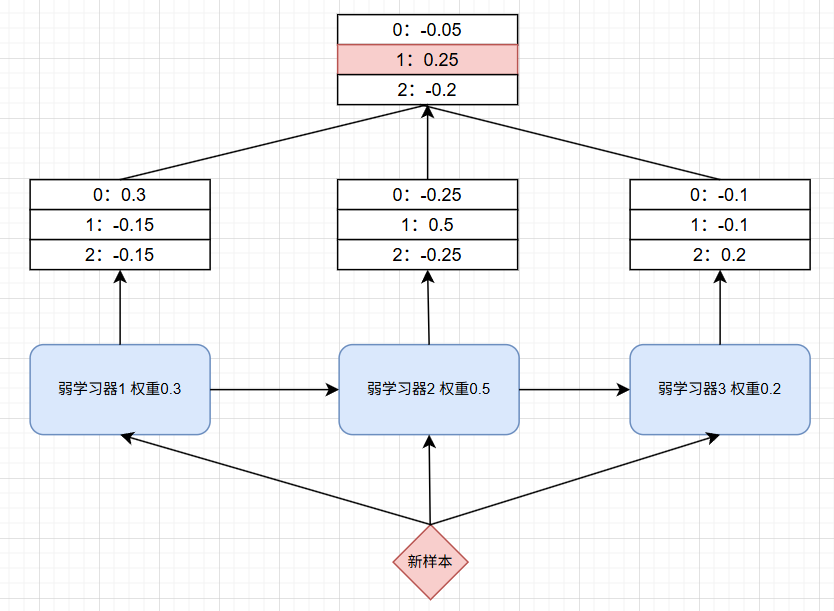
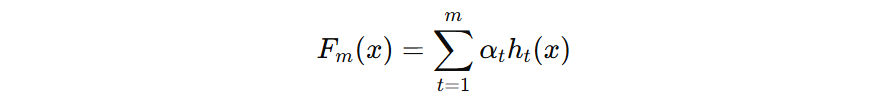
预测过程:
- 每个弱学习器对输入样本的各类别分别打分
- 将所有弱学习器的类别分数按各自模型权重加权求和
- 得分最高的类别即为最终预测结果
1.2 训练过程

AdaBoost 的目标:把一堆单兵作战能力一般的小模型,训练成一个协同作战的强模型。它的秘诀只有两样:样本权重,模型权重。
样本权重是它的引导机制。上一轮弱学习器把某些样本判错了,这些样本的权重就会提高。判对了的样本权重会下降。下一轮训练时,弱学习器会自然把更多精力放在那些前任处理不好的样本上。如此往复,每个弱学习器都在专门修补前一轮的盲点。
但小模型之间也有水平高低。有的弱学习器确实学到了东西,有的则只是混了一下训练流程。这就需要模型权重来分配话语权:表现好的弱学习器权重大、影响力强。表现差的弱学习器被自动降权,避免它们把整体结果带偏。
整个训练可以这样概括:
- 初始样本权重全部相同
- 用当前样本权重训练弱学习器
- 根据弱学习器的错误率计算模型权重
- 根据该弱学习器的预测结果更新样本权重,让误分样本在下一轮更显眼
- 重复上述步骤,逐步累积多个弱学习器
说到底,AdaBoost 的训练像是一场接力赛,每一棒都试图弥补上一棒留下的漏洞,最终把这些不那么完美的弱选手,组合成一个尽可能可靠的强模型。
下面对重要概念进行总结:
- 核心思想:通过组合多个弱学习器,逐步提升整体分类性能,训练过程是串行的,每一轮都依赖上一轮的结果
- 样本权重:通过动态调整样本权重,让分类错误或难分的样本在下一轮获得更高关注度。
- 模型权重:每个弱学习器都被赋予一个模型权重,表示其重要性,权重越大,对最终预测影响越强
- 预测方式:最终预测由所有弱学习器的加权投票得到
- 弱学习器:通常使用非常简单的模型,性能略优于随机猜测,能有效避免过拟合
2. 公式推导
前面对算法训练过程的描述都只是思路,到底错一个样本,样本权重该涨多少?模型权重应该怎么计算?这些问题全靠猜或者拍脑袋,算法就没法落地。
为了让样本权重怎么调、模型权重怎么定都变成精确而可执行的规则,我们需要进行公式推导,把这些口头的直觉,变成清晰的数学步骤,让 AdaBoost 的机制从想法变成算法。
2.1 目标函数
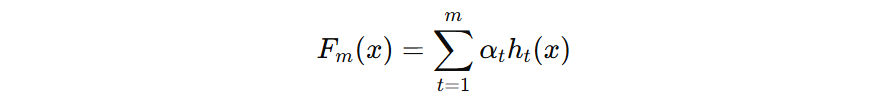
其中:
- \( F_{m}(x) \) 也是一个 \( K \) 维的向量,表示每个类别预测得分
- \(\alpha_{t}\) 表示第 t 个弱分类器的权重
- \( h_{t}(x) \) 表示弱分类器输出的类别标签
假设共有 \(K\) 个类别,输出类别为 \(c\),我们将其编码为一个 \(k\) 维的向量 \(y=(y_{1}…y_{k})\) ,则:
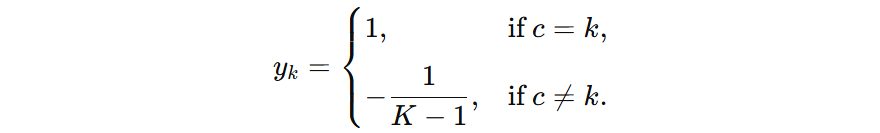
假设有 \( 3 \)个类别,假设某个样本的真实标签为:
- 如果标签 1 时,可示为 \( (1, -\frac{1}{2}, -\frac{1}{2}) \) 向量。
- 如果标签 2 时,可示为 \( (-\frac{1}{2}, 1, -\frac{1}{2}) \) 向量。
- 如果标签 3 时,可示为 \( (-\frac{1}{2}, -\frac{1}{2}, 1) \) 向量。
AdaBoost 的目标是最小化加权指数损失,单个样本的损失表示可表示为:
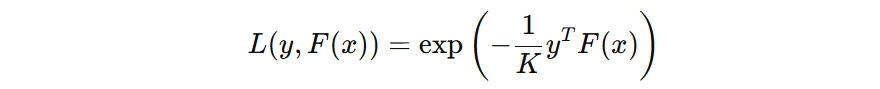
假设:真实标签 \(y\) 为: \((1, -1/2, -1/2)\)
- 如果预测正确,\( F_{m}(x) \) 输出分数为:\((0.8, -0.4, -0.4)\),则指数损失为:0.67
- 如果预测错误,\( F_{m}(x) \) 输出分数为:\((-0.4, 0.8, -0.4)\),则指数损失为:1.22
并且,预测正确的分数越大,则损失越小。预测错误的分数越大,则损失越大。所有训练样本的损失表示如下,我们优化的目标就是得到每个弱学习器的权重,从而使得正确类别预测的分数尽可能的大。
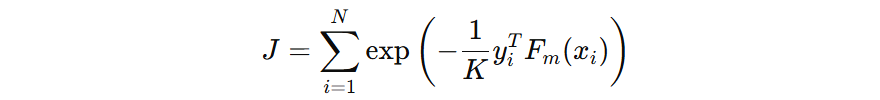
2.2 模型权重
在第 \( m \) 轮的输出,可以由下面的公式表示:
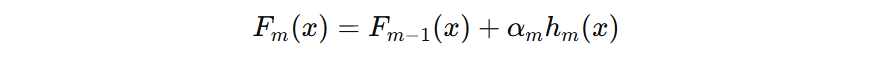
我们的损失函数可以表示为:
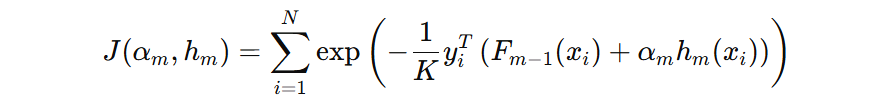
将目标函数展开:
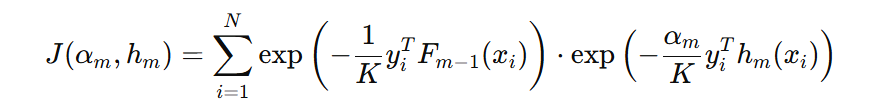
上述公式中:
- 第一项:表示第 i 个样本在 m 弱学习器的损失时的样本权重,权重的大小由前面弱学习器对该样本的预测情况来决定,如果预测正确,并且预测正确分数较高,则权重较低。如果预测错误,则预测错误分数越高,则权重越高。
- 第二项:表示第 i 个样本在 m 弱学习器的损失
我们把第一项样本权重使用 \( w_{i}(m) \) 表示,则得到公式:
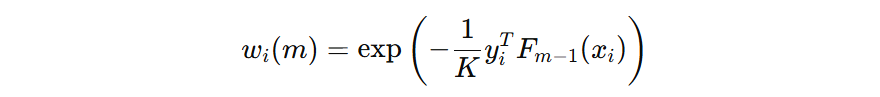
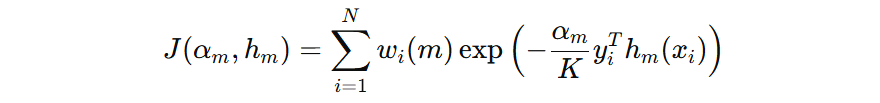
样本权重是由上一个弱学习器的预测结果来确定的。如果上一轮弱学习器预测错误,则样本的权重在下一轮中会相应增大。反之,若预测正确,样本权重会减小。这样,新的弱学习器在训练时会更加关注那些此前被错误分类的样本,从而逐步提升整体模型的分类性能。
损失函数是由分类正确的样本的损失、分类错误样本的损失构成,因此目标函数可以写成:
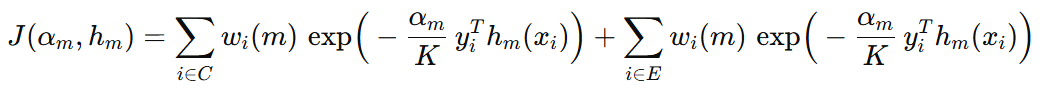
接下来,我们推导一下 \( y_{i}^{T}h_{m}(x_{i}) \) 在预测正确和错误时的结果是什么。假设预测正确,则真实标签和模型预测标签可以表示如下:
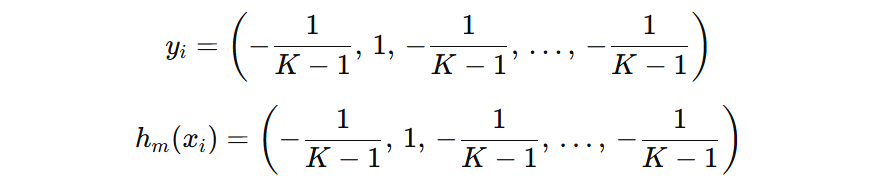
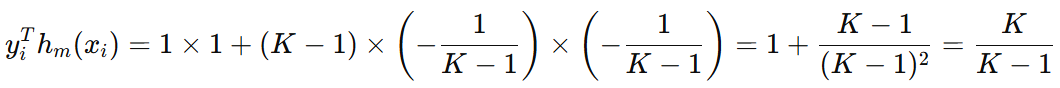
那么,如果预测错误的话:
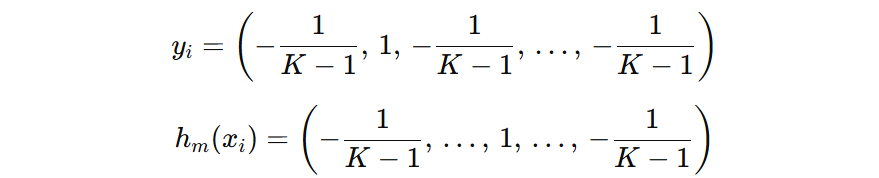
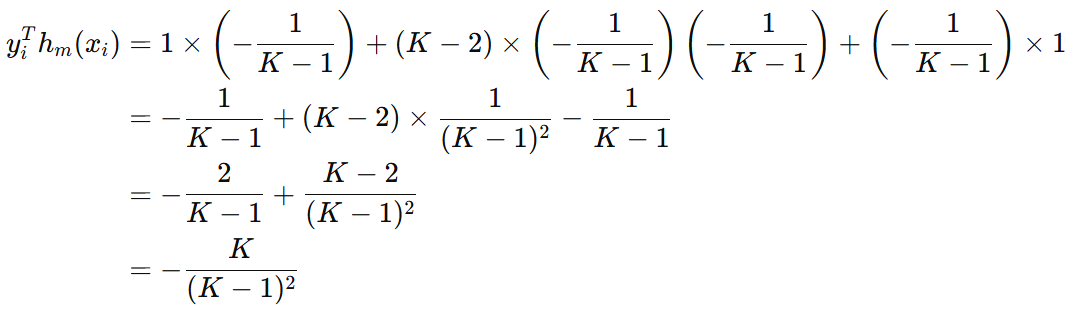
把分类正确、分类错误时得到的公式代入原来损失函数,得到下面的公式:
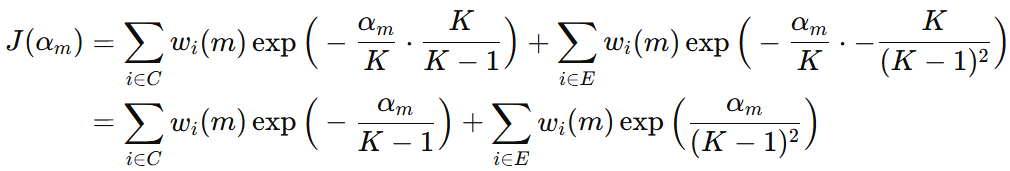
我们希望知道当前弱学习器的权重 \( \alpha_{m} \) 是什么,才能使得损失函数最小。接下来,对 \( \alpha_{m} \) 进行求导,并令导数为 0,再化简之后,得到下面的公式:
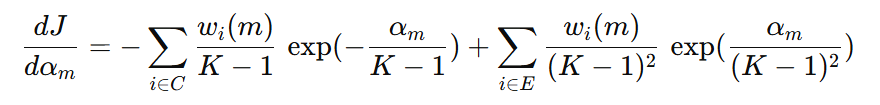
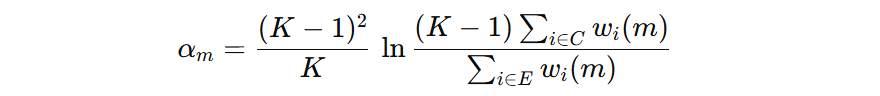
我们看到,分母表示错误样本的权重,表示当前弱学习器的加权错误率。我们用 \( err_{t} \) 来表示分母的加权错误率,则分子加权正确率可以表示为 \( 1- err_{t} \)。
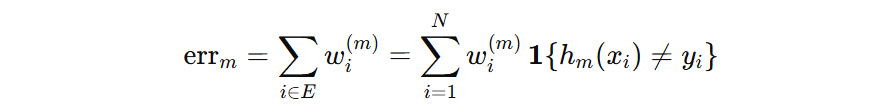
我们再把前面的系数 \( \frac{(K-1)^2}{K} \) 去掉,则得到模型的权重计算公式:
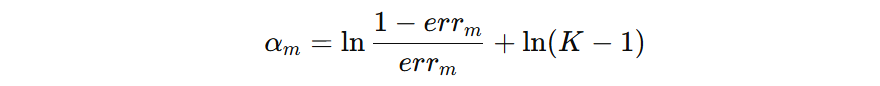
在三分类场景中,随机猜测的准确率为 1/3,对应错误率为1−1/3 ≈ 0.67。若某弱学习器的错误率高于此(如取 err = 0.68),代入多分类 AdaBoost 的权重公式,计算得模型权重约为−0.06。
这一结果揭示了 AdaBoost 的核心约束:算法要求每个弱学习器的错误率必须低于随机猜测的错误率(即二分类中 err < 0.5,多分类中 err <1−1/K)。若弱学习器无法满足这一条件,其权重会为负,纳入集成后反而会降低模型性能。因此,AdaBoost 在迭代训练时,若找不到错误率低于随机猜测的弱学习器,会直接停止训练。
2.3 样本权重
每一轮弱学习器训练时,样本的权重是由前面弱学习器的预测情况来确定:
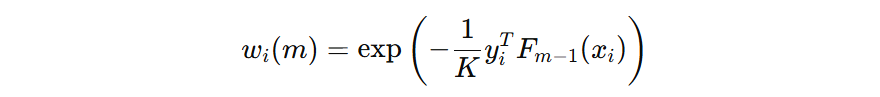
当前弱学习器训练完成之后,下一轮弱学习器训练时的样本权重可以用下面的公式表示:
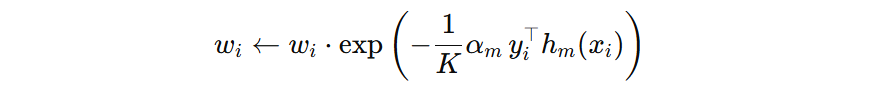
我们把前面得到的 \( y_{i}^{T}h_{m}(x_{i}) \) 代入到公式中,可得下一轮样本权重的更新公式(注意:这是未归一化的权重):
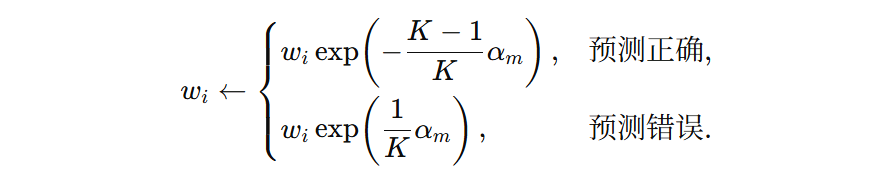
我们让两者都乘以相同的常数 \( \exp\left(\frac{K-1}{K}\,\alpha_m\right) \),则可得:
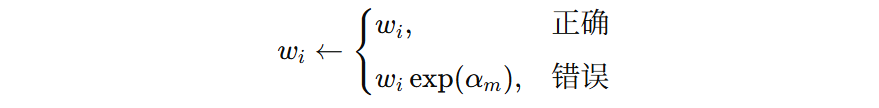
这个公式表示:当前弱学习器预测正确样本,则样本权重不调整。当预测错误,则样本权重提升。最后,对所有样本的权重进行归一化,即可得到下一轮训练的样本权重。
3. 计算案例
AdaBoost 核心思想是关注错误样本、动态调整权重。每轮训练后,提高被当前弱学习器误分类样本的权重,让后续弱学习器更聚焦于这些难分样本。同时,根据弱学习器的分类精度,为其分配不同权重(精度越高,权重越大),最终通过加权投票得到强学习器。
接下来,以具体案例为核心,拆解完整训练过程,帮助大家理解自适应权重调整的本质。我们采用10 个样本的 3 分类任务,数据如下表所示。特征仅 1 个,类别分为 0、1、2,任务是训练多个弱决策树,实现对样本的分类。
| 样本编号 | 特征 X | 真实类别 |
|---|---|---|
| 1 | 1.0 | 0 |
| 2 | 1.5 | 0 |
| 3 | 2.0 | 0 |
| 4 | 3.0 | 1 |
| 5 | 3.5 | 1 |
| 6 | 4.0 | 1 |
| 7 | 5.0 | 2 |
| 8 | 5.5 | 2 |
| 9 | 6.0 | 2 |
| 10 | 3.8 | 1 |
AdaBoost(SAMME)的训练过程可以总结为以下步骤:
- 初始化:样本权重 = 1/N
- 训练弱决策树(树桩)
- 计算弱学习器错误率
- 计算弱学习器的权重
- 更新下轮样本的权重
- 循环 2-5 步,直到达到停止的条件

3.1 模型起步
训练开始前,因为我们对样本难分程度无先验认知,所以样本的权重均等。样本总数为 10,故每个样本的初始权重为 0.1。
| 样本编号 | 特征 X | 真实标签 | 初始权重 |
|---|---|---|---|
| 1 | 1.0 | 0 | 0.1 |
| 2 | 1.5 | 0 | 0.1 |
| 3 | 2.0 | 0 | 0.1 |
| 4 | 3.0 | 1 | 0.1 |
| 5 | 3.5 | 1 | 0.1 |
| 6 | 4.0 | 1 | 0.1 |
| 7 | 5.0 | 2 | 0.1 |
| 8 | 5.5 | 2 | 0.1 |
| 9 | 6.0 | 2 | 0.1 |
| 10 | 3.8 | 1 | 0.1 |
3.2 首次训练
我们基于这些带权重的样本训练第一个弱决策树,核心是找一个切分点。在 scikit-learn 1.7.2 中决策树的构建默认使用 gini 分裂增益计算方法。我们以 4.5 为例,将训练集分为两部分:
| 样本编号 | 特征 X | 真实标签 | 初始权重 |
|---|---|---|---|
| 1 | 1.0 | 0 | 0.1 |
| 2 | 1.5 | 0 | 0.1 |
| 3 | 2.0 | 0 | 0.1 |
| 4 | 3.0 | 1 | 0.1 |
| 5 | 3.5 | 1 | 0.1 |
| 6 | 4.0 | 1 | 0.1 |
| 7 | 5.0 | 2 | 0.1 |
| 8 | 5.5 | 2 | 0.1 |
| 9 | 6.0 | 2 | 0.1 |
| 10 | 3.8 | 1 | 0.1 |
接下来计算该分裂的分类增益:
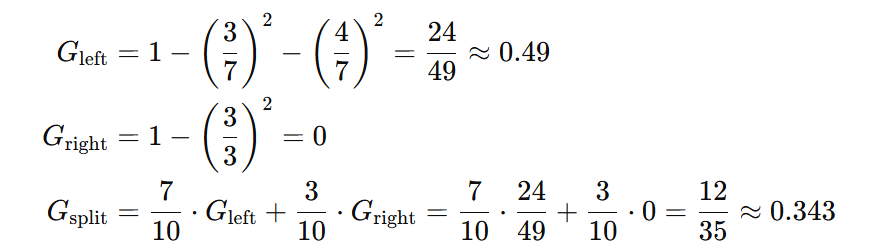
基尼不纯度计算方法:https://mengbaoliang.cn/archives/84678/
我们按照相同的方法,计算所有候选切分点的加权基尼不纯度,选择值最小的点进行此次分裂。
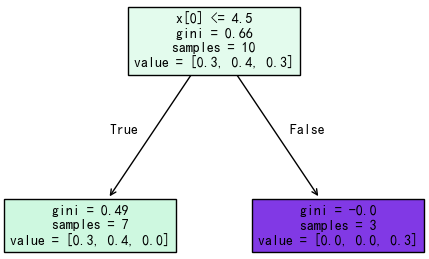
接下来,基于下面的公式计算模型的错误率。错误样本共 3 个,其权重和为 0.1+0.1+0.1=0.3,所以该模型的错误率为:0.3。
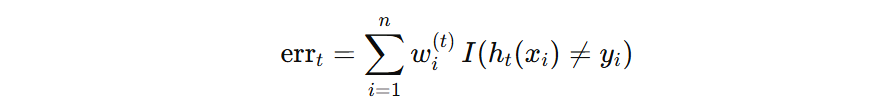
| 样本编号 | 特征 X | 真实标签 | 初始权重 | 预测标签 |
|---|---|---|---|---|
| 1 | 1.0 | 0 | 0.1 | 1 – × |
| 2 | 1.5 | 0 | 0.1 | 1 – × |
| 3 | 2.0 | 0 | 0.1 | 1 – × |
| 4 | 3.0 | 1 | 0.1 | 1 – √ |
| 5 | 3.5 | 1 | 0.1 | 1 – √ |
| 6 | 4.0 | 1 | 0.1 | 1 – √ |
| 7 | 5.0 | 2 | 0.1 | 2- √ |
| 8 | 5.5 | 2 | 0.1 | 2- √ |
| 9 | 6.0 | 2 | 0.1 | 2- √ |
| 10 | 3.8 | 1 | 0.1 | 1- √ |
在前面公式推导的时候,我们并没有引入学习率的概念。在 AdaBoost 中,学习率用于控制单个弱分类器权重贡献程度,它决定了弱分类器对最终模型的影响幅度。
- η 越小,单个弱分类器的权重越低,模型收敛越慢,但可能更稳定
- η 越大,单个弱分类器的权重越高,模型收敛越快,但容易过拟合
如果没有学习率,假设模型受到异常、噪声的影响,导致某个模型话语权太大, 一旦它判断失误,对最终结果影响太大了。
我们在计算模型权重时,已经把学习率作用到模型的权重的计算中(\( \eta=0.3、K=3、err_{t}=0.3 \)):
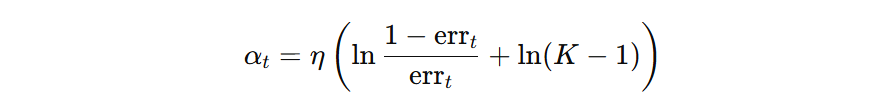
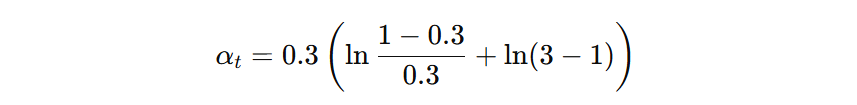
最终计算得到第一个弱学习器的权重为:0.4621。注意:学习率直接计算到模型权重上了。
接着,更新样本的权重。如果之前对该样本预测错误,则提高样本权重,否则权重不变。然后重新归一化,得到第二轮迭代需要的样本权重。
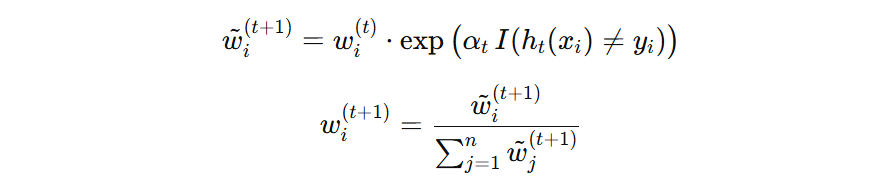
计算举例:
- 1号样本预测错误,则其权重为:\( 0.1 \times \exp(0.4621) = 0.15874 \)
- 4号样本预测正确,则其权重为:\( 0.1 \times \exp(0) = 0.1 \)
以此类推,计算所有样本新的权重,然后再归一化,如下图所示:
| 样本编号 | 特征 X | 真实类别 | 预测类别 | 更新权重分数 | 归一化权重 |
|---|---|---|---|---|---|
| 1 | 1.0 | 0 | 1 – × | 0.15875 | 0.13496 |
| 2 | 1.5 | 0 | 1 – × | 0.15875 | 0.13496 |
| 3 | 2.0 | 0 | 1 – × | 0.15875 | 0.13496 |
| 4 | 3.0 | 1 | 1 – √ | 0.1 | 0.08502 |
| 5 | 3.5 | 1 | 1 – √ | 0.1 | 0.08502 |
| 6 | 4.0 | 1 | 1 – √ | 0.1 | 0.08502 |
| 7 | 5.0 | 2 | 2- √ | 0.1 | 0.08502 |
| 8 | 5.5 | 2 | 2- √ | 0.1 | 0.08502 |
| 9 | 6.0 | 2 | 2- √ | 0.1 | 0.08502 |
| 10 | 3.8 | 1 | 1 – √ | 0.1 | 0.08502 |
我们会发现:样本权重的更新依赖模型权重,而学习率已经作用到模型权重中,相当于间接影响了样本权重的计算。较大的学习率,模型的权重较大,误分类样本权重会较大幅度调整,反之,样本的权重调整幅度较小,模型的训练过程也相对保守一些。
3.3 持续优化
基于新的样本权重权重训练第二个弱学习器:
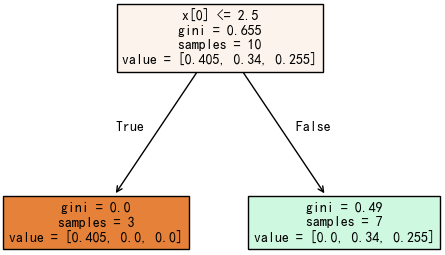
计算当前弱学习器的错误率,错误的样本为 7、8、9,其权重和为:\( 0.08502 + 0.08502 + 0.08502 = 0.25506 \)
| 样本编号 | 特征 X | 真实标签 | 归一化权重 | 预测标签 |
|---|---|---|---|---|
| 1 | 1.0 | 0 | 0.13496 | 0 – √ |
| 2 | 1.5 | 0 | 0.13496 | 0 – √ |
| 3 | 2.0 | 0 | 0.13496 | 0 – √ |
| 4 | 3.0 | 1 | 0.08502 | 1 – √ |
| 5 | 3.5 | 1 | 0.08502 | 1 – √ |
| 6 | 4.0 | 1 | 0.08502 | 1 – √ |
| 7 | 5.0 | 2 | 0.08502 | 1 – × |
| 8 | 5.5 | 2 | 0.08502 | 1 – × |
| 9 | 6.0 | 2 | 0.08502 | 1 – × |
| 10 | 3.8 | 1 | 0.08502 | 1 – √ |
接着计算当前弱学习器的权重(0.5295):
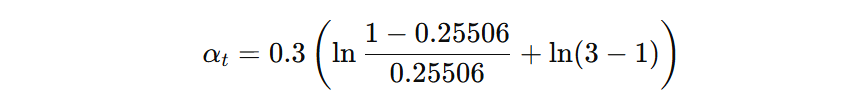
最后,更新样本权重(省略计算过程),循环迭代构建多个弱学习器。
当满足以下条件时,停止训练:
- 当构建的弱学习器数量达到指定的数量,停止训练
- 当构建的弱学习器错误率为 0 时,已经能够正确区分所有样本,停止训练
- 当弱学习器的错误率高于随机猜测的错误率 \(1-1/K\) 时,模型的权重是负值,那么样本的权重在更新时,分类错误样本权重会降低,分类正确的样本权重会上升,这使得继续训练会产生更大的错误,所以停止训练。




 冀公网安备13050302001966号
冀公网安备13050302001966号