AdaBoost(Adaptive Boosting,自适应提升)是集成学习中极具代表性的算法,其核心思想是关注错误样本、动态调整权重。每轮训练后,提高被前一轮弱学习器误分类样本的权重,让后续弱学习器更聚焦于这些难分样本。同时,根据弱学习器的分类精度,为其分配不同权重(精度越高,权重越大)。最终通过加权投票得到强学习器。接下来,以具体案例为核心,拆解 SAMME 的完整训练过程,帮助大家理解自适应权重调整的本质。
为了让大家更直观理解,我们采用10 个样本的 3 分类任务,数据如下表所示。特征仅 1 个,类别分为 0、1、2,任务是训练多个弱决策树,实现对样本的分类。
| 样本编号 | 特征 X | 真实类别 |
|---|---|---|
| 1 | 1.0 | 0 |
| 2 | 1.5 | 0 |
| 3 | 2.0 | 0 |
| 4 | 3.0 | 1 |
| 5 | 3.5 | 1 |
| 6 | 4.0 | 1 |
| 7 | 5.0 | 2 |
| 8 | 5.5 | 2 |
| 9 | 6.0 | 2 |
| 10 | 3.8 | 1 |

AdaBoost(SAMME)的训练过程可以总结为以下步骤:
- 计算样本的权重
- 训练弱决策树,默认构建高度为1的树
- 计算弱决策树的错误率
- 计算弱决策树的权重
- 循环 1-4 步,直到达到提前停止的条件
1. 第一轮迭代
训练开始前,因为我们对样本难分程度无先验认知,所以样本的权重均等。样本总数为 10,故每个样本的初始权重为 0.1。
| 样本编号 | 特征 X | 真实标签 | 初始权重 |
|---|---|---|---|
| 1 | 1.0 | 0 | 0.1 |
| 2 | 1.5 | 0 | 0.1 |
| 3 | 2.0 | 0 | 0.1 |
| 4 | 3.0 | 1 | 0.1 |
| 5 | 3.5 | 1 | 0.1 |
| 6 | 4.0 | 1 | 0.1 |
| 7 | 5.0 | 2 | 0.1 |
| 8 | 5.5 | 2 | 0.1 |
| 9 | 6.0 | 2 | 0.1 |
| 10 | 3.8 | 1 | 0.1 |
我们基于这些带权重的样本训练第一个弱决策树,核心是找一个切分点,将样本分为两类。针对当前样本权重,训练得到的最优切分点为:X≤4.5 的样本为一组,X>4.5 的为另一组,如下图所示:
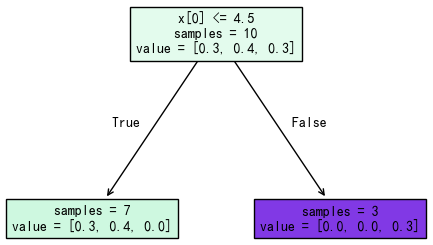
为了得到模型的错误率,需要判断每个样本的预测结果是否正确,然后基于下面的公式计算模型的错误率。错误样本共 3 个,其权重和为 0.1+0.1+0.1=0.3,所以该模型的错误率为:0.3。
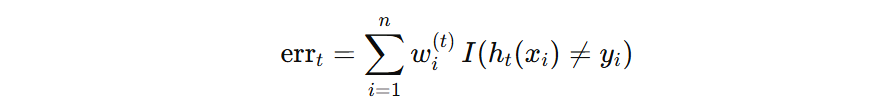
| 样本编号 | 特征 X | 真实标签 | 初始权重 | 预测标签 |
|---|---|---|---|---|
| 1 | 1.0 | 0 | 0.1 | 1 – × |
| 2 | 1.5 | 0 | 0.1 | 1 – × |
| 3 | 2.0 | 0 | 0.1 | 1 – × |
| 4 | 3.0 | 1 | 0.1 | 1 – √ |
| 5 | 3.5 | 1 | 0.1 | 1 – √ |
| 6 | 4.0 | 1 | 0.1 | 1 – √ |
| 7 | 5.0 | 2 | 0.1 | 2- √ |
| 8 | 5.5 | 2 | 0.1 | 2- √ |
| 9 | 6.0 | 2 | 0.1 | 2- √ |
| 10 | 3.8 | 1 | 0.1 | 1- √ |
模型的权重根据下面公式计算即可(\( \eta=0.3、K=3、err_{t}=0.3 \)):
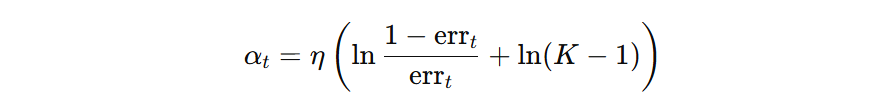
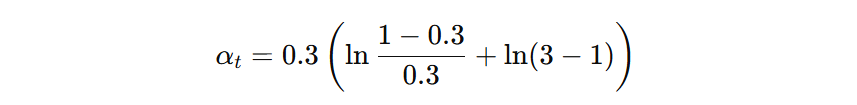
最终计算得到第一个弱学习器的权重为:0.4621
在这里需要注意下,学习率直接计算到模型权重上了。另外,较大的学习率,使得样本的权重的调整幅度较大,模型的训练过程也就较为激进,反之,样本的权重调整幅度较小,模型的训练过程也相对保守一些。
2. 第二轮迭代
如果之前对该样本预测错误,则提高样本权重,否则权重不变。然后重新归一化,得到第二轮迭代需要的样本权重。
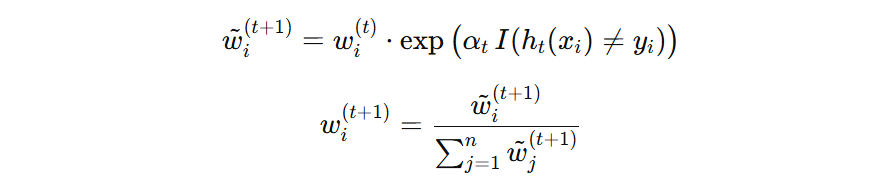
计算举例(上一次迭代模型权重为:0.4621)
- 1号样本预测错误,则其权重为:\( 0.1 \times \exp(0.4621) = 0.15874 \)
- 4号样本预测正确,则其权重为:\( 0.1 \times \exp(0) = 0.1 \)
以此类推,计算所有样本新的权重,然后再归一化,如下图所示:
| 样本编号 | 特征 X | 真实类别 | 预测类别 | 更新权重分数 | 归一化权重 |
|---|---|---|---|---|---|
| 1 | 1.0 | 0 | 1 – × | 0.15875 | 0.13496 |
| 2 | 1.5 | 0 | 1 – × | 0.15875 | 0.13496 |
| 3 | 2.0 | 0 | 1 – × | 0.15875 | 0.13496 |
| 4 | 3.0 | 1 | 1 – √ | 0.1 | 0.08502 |
| 5 | 3.5 | 1 | 1 – √ | 0.1 | 0.08502 |
| 6 | 4.0 | 1 | 1 – √ | 0.1 | 0.08502 |
| 7 | 5.0 | 2 | 2- √ | 0.1 | 0.08502 |
| 8 | 5.5 | 2 | 2- √ | 0.1 | 0.08502 |
| 9 | 6.0 | 2 | 2- √ | 0.1 | 0.08502 |
| 10 | 3.8 | 1 | 1 – √ | 0.1 | 0.08502 |
基于该权重训练第二个弱学习器(树桩)
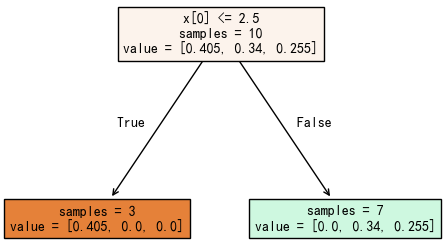
判断每个样本的预测结果,计算错误样本的权重和(弱学习器加权错误率)。错误的样本为 7、8、9,其权重和为:\( 0.08502 + 0.08502 + 0.08502 = 0.25506 \)
| 样本编号 | 特征 X | 真实标签 | 归一化权重 | 预测标签 |
|---|---|---|---|---|
| 1 | 1.0 | 0 | 0.13496 | 0 – √ |
| 2 | 1.5 | 0 | 0.13496 | 0 – √ |
| 3 | 2.0 | 0 | 0.13496 | 0 – √ |
| 4 | 3.0 | 1 | 0.08502 | 1 – √ |
| 5 | 3.5 | 1 | 0.08502 | 1 – √ |
| 6 | 4.0 | 1 | 0.08502 | 1 – √ |
| 7 | 5.0 | 2 | 0.08502 | 1 – × |
| 8 | 5.5 | 2 | 0.08502 | 1 – × |
| 9 | 6.0 | 2 | 0.08502 | 1 – × |
| 10 | 3.8 | 1 | 0.08502 | 1 – √ |
接着计算第二个弱学习器的权重(0.5295):
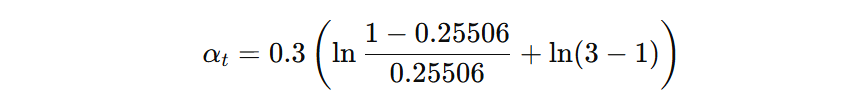
循环迭代构建多个弱学习器:
- 当构建的弱学习器数量达到指定的数量,停止训练
- 当构建的弱学习器错误率为 0 时,已经能够正确区分所有样本,停止训练
- 当弱学习器的错误率高于随机猜测 \(1-1/K\) 时,模型的权重是负值,那么样本的权重在更新时,分类错误样本权重会降低,分类正确的样本权重会上升,这使得继续训练会产生更大的错误,所以停止训练。

 冀公网安备13050302001966号
冀公网安备13050302001966号