AdaBoost（SAMME）预测过程

在这节我们通过一个具体的小例子，来理解 AdaBoostClassifier 是如何在多分类问题中做出预测的，重点是弄清楚：

每个弱学习器是怎么打分的
最终得分是怎么组合出来的
为什么权重大的弱学习器影响更大

假设我们有如下样本：

样本编号	特征 X	真实类别
1	1.0	0
2	1.5	0
3	2.0	0
4	3.0	1
5	3.5	1
6	4.0	1
7	5.0	2
8	5.5	2
9	6.0	2
10	3.8	1

我们让 AdaBoost 去学习这个三分类任务（类别 0、1、2）。弱学习器使用深度为 1 的决策树桩，训练 3 个弱学习器，学习率为 0.3。

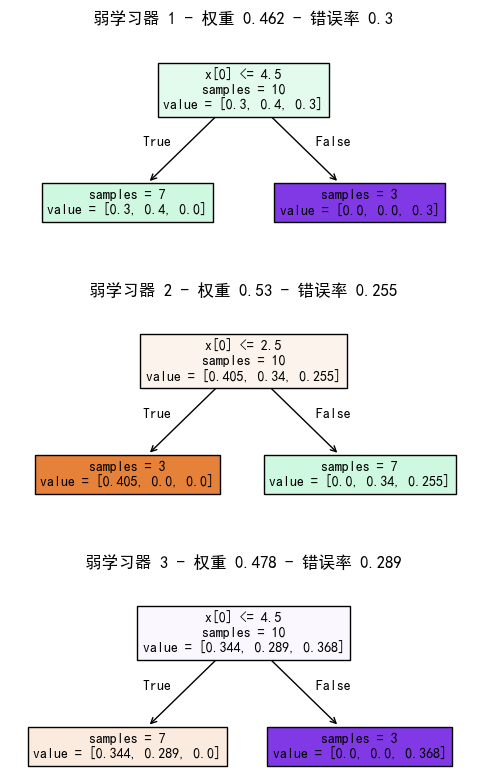
假设来了一个新样本 [2.5]，我们需要预测它的类别。AdaBoost 的预测是基于加法模型 + 加权投票的思想：

每个弱学习器在预测时，对自己认为正确的类别加分，对其他类别减分
最终将所有弱学习器的打分加权求和，分数最高的类别就是预测结果

为什么要对其他类别减分？

在 AdaBoost 中，每个弱学习器为每个类别打分，表示它对该类别的信心。正分数表示该类别可能正确，负分数表示该类别可能不对，分数越大，学习器的信心越强。

弱学习器的权重决定了它对分类结果的影响力。权重越大的弱学习器，对它认为正确类别的打分会越高，同时对它认为不正确类别的负分也会越大。这种设计有其合理性：如果第一个弱学习器的权重大，它对某个类别的否定（即给负分）就会带来更大的惩罚。即使后续的弱学习器试图纠正（通过给出正分），由于它们的权重较小，影响力不足，无法完全改变第一个大权重学习器的判断。

具体来说：对于一个新样本 \(x\)，第 \(t\) 个弱学习器的输出记作 \(h_{t}(x)\)，它的权重为 \(α_{t}\)。那么该学习器的打分向量为：

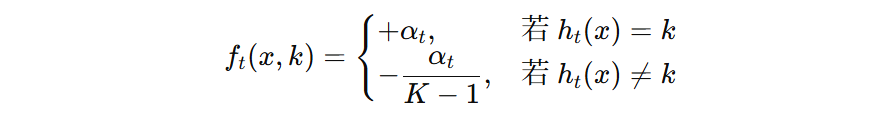
我们根据该公式，可以计算出每个弱学习器对新样本的打分向量：

第一个弱学习器的分数向量：[-0.23106676 0.46213351 -0.23106676]
第二个弱学习器的分数向量：[ 0.52950045 -0.26475023 -0.26475023]
第三个弱学习器的分数向量：[ 0.47849894 -0.23924947 -0.23924947]

回过头来，我们再看公式中，预测错误时，为什么打的负分是 \( -\alpha_{t} / (K – 1) \) ？

我们可以这么理解，AdaBoost 想要表达得是，弱学习器有多肯定 0 类别，就有多否定非 0 的类别。这是一个弱学习器的话语权，它既能够对“是”进行强度表示，同时也能够对“否”进行强度表示，分数就是表示这种强度的，所以当肯定某个类别的分数是 0.8 时，否定其他类别的总分数也是 -0.8，假设共有 3 个类别，那么其他的类别分别承担 -0.4 的否定分数。

接下来，将对应类别的分数加起来，得到 AdaBoost 对各个类别的打分：[ 0.77693263 -0.04186618 -0.73506645]，我们可以看到，1 类别分数最大，所以，[2.5] 最终归类为 1 类别。

from sklearn.ensemble import AdaBoostClassifier
import numpy as np
from sklearn.tree import plot_tree
import matplotlib.pyplot as plt


def demo():
    # 1. 数据准备
    X = [[1.0], [1.5], [2.0], [3.0], [3.5], [4.0], [5.0], [5.5], [6.0], [3.8]]
    y = [0, 0, 0, 1, 1, 1, 2, 2, 2, 1]

    # 2. 模型训练
    # 弱学习器默认使用高度为 1 的决策树
    adaboost = AdaBoostClassifier(n_estimators=3, learning_rate=0.3, random_state=42)
    adaboost.fit(X, y)

    # 弱决策树可视化
    fig, axes = plt.subplots(3, 1, figsize=(6, 10))
    for i, (estimator, weight, error, ax) in enumerate(zip(adaboost.estimators_, adaboost.estimator_weights_, adaboost.estimator_errors_, axes)):
        plot_tree(estimator, fontsize=10, filled=True, impurity=False, proportion=False, ax=ax)
        ax.set_title(f"弱学习器 {i + 1} 权重 {round(weight, 3)} 错误率 {round(error, 3)}")
    plt.show()


    print('弱学习器错误率:', adaboost.estimator_errors_)
    # 弱学习器权重 = 学习率 * 弱学习器原本权重
    print('弱学习器的权重:', adaboost.estimator_weights_)

    # 3. 新样本预测
    new_x = [[2.5]]
    n_classes = len(adaboost.classes_)

    # 3.1 内部计算
    y_score = adaboost.decision_function(new_x)
    y_label = adaboost.predict(new_x)
    print('内部计算:', '各个类别预测分数:', y_score.squeeze(), '最终预测标签', y_label.squeeze())

    # 3.2 手动计算
    # 累计每个类别预测得分
    y_score = np.zeros(n_classes, dtype=np.float64)
    for estimator, weight in zip(adaboost.estimators_, adaboost.estimator_weights_):
        # 弱分类器预测结果（例如 [1]）
        stage_label = estimator.predict(new_x)
        # 投票规则：
        # 对预测到的类别 +weight，
        # 对未预测的类别 -weight / (K - 1)
        stage_score = np.where(adaboost.classes_ == stage_label[0], weight, -weight / (n_classes - 1))
        print(f"预测类别={stage_label[0]}, 权重={weight:.3f}, 投票分数={stage_score}")
        y_score += stage_score

    print('最终打分:', y_score)
    # 归一化（我们在前面的例子中，并没有做这一步，这一步不会影响最终预测结果）
    y_score = y_score / adaboost.estimator_weights_.sum()
    y_label = adaboost.classes_[np.argmax(y_score)]

    print('手动计算:', '各个类别预测分数:', y_score, '最终预测标签', y_label)


if __name__ == '__main__':
    demo()

弱学习器错误率: [0.3        0.2550506  0.28867062]
弱学习器的权重: [0.46213351 0.52950045 0.47849894]
内部计算: 各个类别预测分数: [ 0.52847782 -0.02847782 -0.5       ] 最终预测标签 0
预测类别=1, 权重=0.462, 投票分数=[-0.23106676  0.46213351 -0.23106676]
预测类别=0, 权重=0.530, 投票分数=[ 0.52950045 -0.26475023 -0.26475023]
预测类别=0, 权重=0.478, 投票分数=[ 0.47849894 -0.23924947 -0.23924947]
手动计算: 各个类别预测分数: [ 0.52847782 -0.02847782 -0.5       ] 最终预测标签 0

AdaBoost（SAMME）预测过程

取消回复