相对位置编码（Relative Positional Encoding）

相对位置编码（RPE）是一种用于替代绝对位置编码（Absolute Positional Encoding, APE）的技术。我们知道 Transformer 模型本身是基于自注意力机制（Self-Attention）的，而自注意力机制是无序的，也就是说自注意力机制不会自动捕捉输入序列的位置信息。因此，我们需要让模型感知到输入 Token 之间的顺序关系。实现这一点，除了绝对位置编码，还有接下来要介绍的相对位置编码，当然还有其他的方法。

绝对位置编码一般都是自注意力计算前，加到 token 的 embedding 上，而相对位置编码则是在自注意力计算时引入。例如：我们要进行 token A 对 token B 的自注意力计算，如果使用绝对位置编码的话，位置信息在自注意力计算前就已经融入到两个 token 中了，如下图：

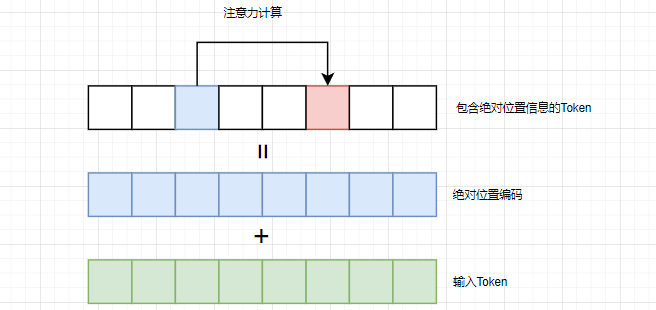
如果使用的是相对位置编码的话，就需要在自注意力计算时，融入位置信息，如下图：

从这个过程，我们也可以看到了相对位置编码在使用时，需要每次动态计算，而绝对位置编码则不需要，性能上后者会好一些。

相对位置编码另外一个优点，是能够适应更长的文本输入。例如：模型支持的最大长度是 128，如果我们使用绝对位置编码就无法对超出训练长度 128 的位置进行位置信息编码。相对位置编码仅考虑两个 token 之间的相对位置，而不是绝对位置。这样可以让模型在不同长度的文本中泛化更好，同时也能更高效地利用长距离依赖关系。

相对位置编码在具体应用到注意力计算时，会有一些不同的计算方式。下面以一种比较简单的实现来介绍下相对位置编码的基本思路。

在《Self-Attention with Relative Position Representations》论文中提出了一种相对位置编码方法。回顾下原始 Transformer 的注意力分数计算：

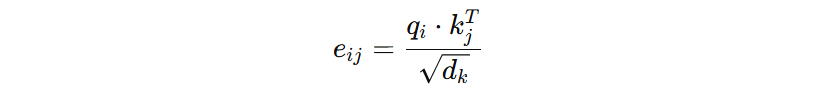
其中：

• \( e_{ij} \) 表示 token i 到 token j 的注意力分数
• \( q_{i} \) 表示 i 位置的 Query 向量
• \( k_{j} \) 表示 j 位置的 Key 向量

在计算注意力分数时引入相对位置向量（\( a_{ij} \)）来增强自注意力计算：

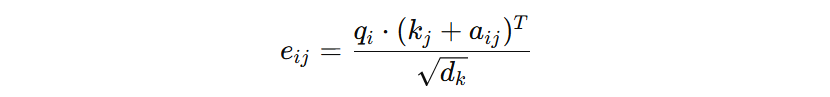
\( a_{ij} \)​ 是一个可学习的相对位置向量，其大小与 \( k_{j} \)​ 相同，表示 token i 和 j 之间的相对位置关系。以此方式，确保 Transformer 在计算 Query 与 Key 之间的点积时能够考虑相对位置信息。

相对距离被限制在一个固定的窗口 \( [−k, k] \) 内，超出该范围的相对距离会被截断（clipped）或映射到最近的边界。例如：最大相对位置窗口 k=8，相对位置 r=j−i，表示 token i 到 token j 的相对距离那么：

• 如果 ∣r∣≤k，相对位置不变
• 如果 r>k，则设为 k（即 +8）
• 如果 r<−k，则设为 −k（即 -8）

这样，Transformer 不会区分那些距离很远的 token，只会关注一定范围内的局部相对位置信息。

在 《Transformer-XL: Attentive Language Models Beyond a Fixed-Length Context》中也提出了另外一种相对位置编码的计算方法。首先，我们先看下基于绝对位置编码的自注意力计算公式：

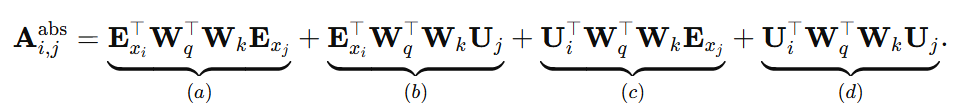
公式中：

• \( E_{xi} \) 表示当前的 token 的内容编码
• \( E_{xj} \) 表示被注意的 token 的内容编码
• \( U_{i} \) 表示当前的位置编码
• \( U_{i} \) 表示被注意的位置编码
• \( W_{q} \) 表示 Query 的学习参数
• \( K_{q} \) 表示 Key 的学习参数

在该 Paper 中，对该计算过程进行了变动：

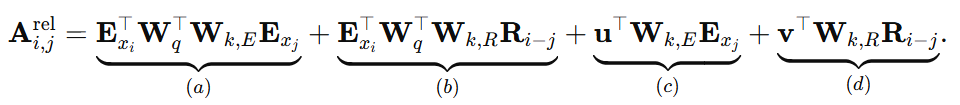
变动如下：

• a 部分：这一部分原来表示当前 token i 的内容对 token j 的注意力计算。 变动：\( W_{k} \) 修改为 \( W_{k, E} \)。
• b 部分：这一部分原来表示当前 token i 的内容对 j 位置的注意力计算。 变动：\( W_{k}U_{j} \) 修改为 \( W_{k, R}R_{i-j} \)
• c 部分：这一部分原来表示当前 i 位置对 token j 内容的注意力计算。 变动：\( U_{i}W_{q}W_{k} \) 修改为 \( uW_{k, E}E_{xj} \)
• d 部分：这一部分原来表示当前 i 位置对 j 位置的注意力计算。变动：\( U_{i}W_{q}W_{k}U_{j} \) 修改为 \( vW_{k, R}R_{i-j} \)

1. 原来的 \( W_{k} \) 变成了 \( W_{k, E} \) 和 \( W_{k, R} \) 分别表示对内容、对相对位置的参数。这说明了什么呢？原来我们获得 Token 的 Key 向量，只需要一个 WK 进行一次变换即可，现在需要使用 \( W_{k, E} \) 和 \( W_{k, R} \) 两个参数计算两个 KEY 向量。
2. 第三项中 i 位置对 j 内容的注意 \( U_{i}W_{q} \)变成了 u。这个变换是什么意思呢？这是因为进行相对位置计算时，当前位置是不变的，是别的 Token 相对我的位置，而我的位置信息似乎并不那么重要，但是当前位置需要进行表示，如何表示？让模型去学习吧，所以这里的 u 就是 i 自己的位置，并且该位置的表示是由模型学习得到的。
3. 第四项中 i 的位置对 j 位置的注意，这里的位置也变成 v 可学习的参数。也就是说，第三项、第四项中的 i 位置的向量表示都变成了固定的可学习位置表示。并且，对内容注意、对位置注意的 i 位置向量是不同的。
4. 另外，第四项中 j 相对位置编码变成了不可学习的固定的由 sin+cos 计算得到的矩阵。当然该矩阵在最原始的位置编码中表示的是绝对位置编码，在这里则表示相对位置编码。

注意：在 transformer-XL 中相对位置编码矩阵是不可学习的，u 和 v 是两个可学习参数。