在 Transformer 模型中，输入的词向量是没有顺序信息的，比如：我爱你 和 你爱我 两个含义不同句子，在注意力计算时，每个 Token 的表示是相同的，即：模型理解这两个句子的含义是相同的，这就很不合理。所以需要通过位置编码来对输入的序列注入顺序信息。

绝对位置编码是向输入序列注入顺序信息的方法之一，它通过给输入序列中的每个位置分配一个唯一的向量来表示位置信息，这个向量是固定的、独立于输入数据的，并与每个输入的词向量相加，这样的话，我爱你 和 你爱我，由于序列顺序不同，每个 Token 的表示就不同，那么模型就可以区分两个句子的不同，使模型能够感知到每个词在序列中的位置。

绝对位置编码通常有两种实现方式：

1. 基于正弦余弦函数：通过使用不同频率的正弦和余弦函数来生成每个位置的编码。这样编码具有某种周期性，使得模型能够处理不同长度的序列。
2. 基于可学习的嵌入：将位置映射到一个学习到的嵌入向量，这些向量在训练过程中与其他模型参数一起优化。

1. 基于正弦余弦函数

正弦余弦位置编码（Sinusoidal Positional Encoding）是一种无需训练的位置编码方法，它通过固定的周期性函数（正弦和余弦）来为序列的不同位置提供唯一的编码。对于每个位置 \( i \) 和每个维度 \( d \)，位置编码通过以下公式计算：

其中：

• \( pos \) 表示位置索引，表示计算哪个位置的编码
• \( i \) 表示编码维度，\( d_{model} \) 是编码空间的总维度
• \( PE_{(pos, 2i)} \) 和 \( PE_{(pos, 2i + 1)} \) 通过正弦和余弦函数分裂映射到偶数和奇数的维度

假设：我们要计算输入序列第 2 个位置 Token 对应的位置编码，编码的维度设定为 4 ，则：

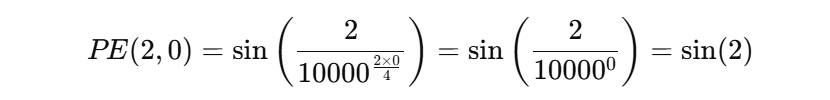
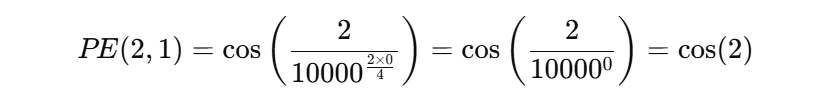
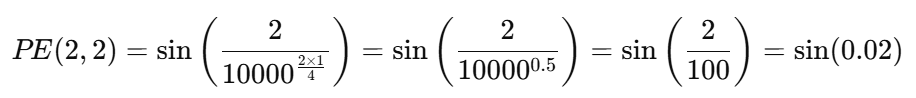
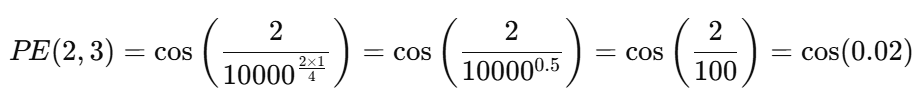
最终，位置 2 的编码向量为：\( (sin(2), cos(2), sin(0.02), cos(0.02)) \)，我们把它加到第二个 Token 的词嵌入向量上，就相当于给其注入了顺序信息。

计算起来是比较容易的，如何去理解这个位置编码？请看下面两张图：

import matplotlib.pyplot as plt
import numpy as np


def sinusoidal_position_encoding(max_len=128, d_model=64):
    position_embedding = np.zeros((max_len, d_model))
    position = np.arange(0, max_len).reshape(-1, 1)
    div_term = 10000.0 ** (np.arange(0, d_model, 2) / d_model)
    # 计算正弦和余弦部分
    position_embedding[:, 0::2] = np.sin(position / div_term)
    position_embedding[:, 1::2] = np.cos(position / div_term)
    return position_embedding


def demo01():
    pe = sinusoidal_position_encoding()
    # 查看: 固定维度，不同位置的编码值可视化
    fixed_dims = [2, 6, 12]
    plt.figure(figsize=(12, 8))
    for idx, (fixed_dim, color) in enumerate(zip(fixed_dims, ['red', 'green', 'brown'])):
        plt.subplot(len(fixed_dims), 1, idx + 1)
        plt.plot(range(128), pe[:, fixed_dim], marker='o', color=color)
        plt.xlim(0, 128)
        if idx < len(fixed_dims) - 1:
            plt.xticks([])
        plt.grid()
    plt.show()


def demo02():
    pe = sinusoidal_position_encoding()
    plt.figure(figsize=(12, 8))

    positions = [1, 5]
    for idx, (position, color) in enumerate(zip(positions, ['red', 'blue'])):
        x_vals = range(32)
        sin_vals = pe[position, 0::2]
        cos_vals = pe[position, 1::2]
        plt.plot(x_vals, sin_vals, marker='o', color=color)
        plt.plot(x_vals, cos_vals, marker='o', color=color)

        plt.text(x_vals[0]+0.1, sin_vals[0], f'sin-{position}', color=color, fontsize=12, verticalalignment='bottom', horizontalalignment='left')
        plt.text(x_vals[0]+0.1, cos_vals[0], f'cos-{position}', color=color, fontsize=12, verticalalignment='top', horizontalalignment='left')

    plt.grid()
    plt.xticks(range(0, 32), range(0, 32))
    plt.xlim(-1, 32 + 1)
    plt.show()


if __name__ == '__main__':
    demo01()
    demo02()

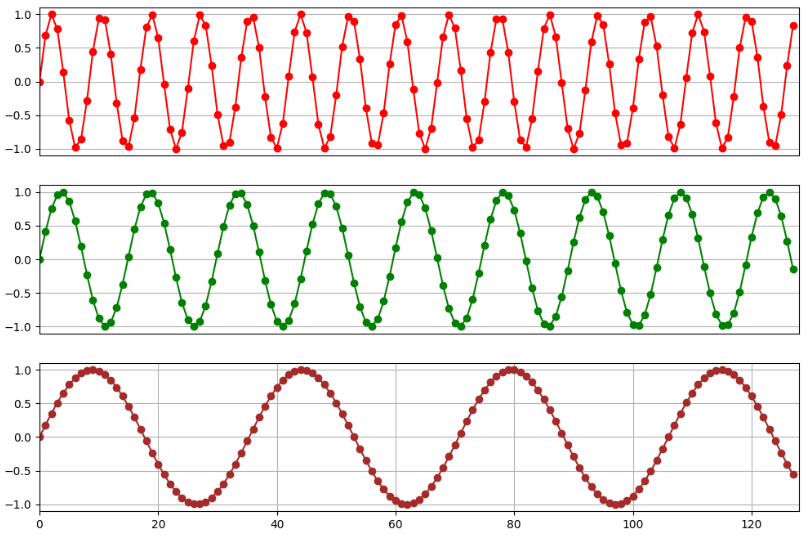
这三张图分别打印了 128 个位置向量第 2、6、12 维度的编码值的变化，我们发现这些值呈现周期性的变化。另外，我们也可以发现，向量维度越高，其周期就越长。

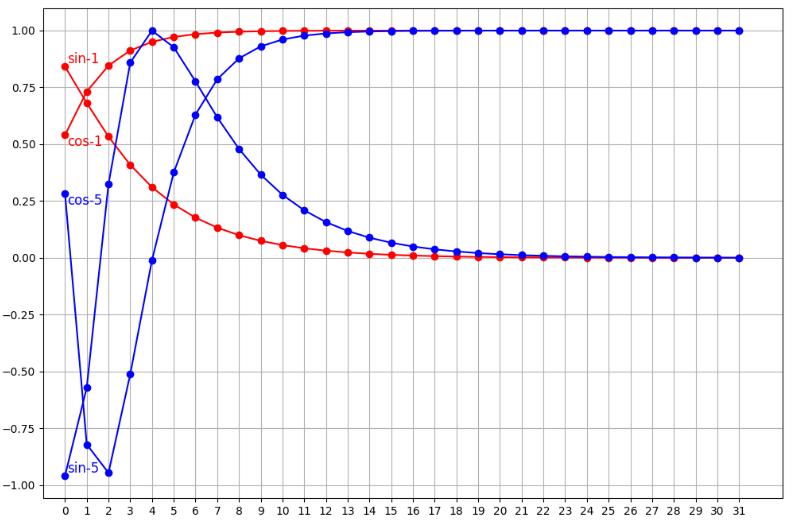
上图，我们打印了位置 1、5 的编码向量中的 sin 和 cos 计算得到的编码值。我们可以发现，基于正弦和余弦函数得到的位置编码可以保证唯一性。另外，也可以看到，向量的维度越高，编码值的波动就越小，向量就越接近。

简单总结下：

• 因为正弦和余弦函数都是周期函数，编码在不同维度上具有不同的周期性
• 位置编码向量是唯一的，因为不同位置的编码由不同的正弦和余弦值组成
• 低维度的编码值波动性很大（周期短），高纬度的编码值波动性较小（周期长）

所以，可以得到一个简单的结论：

• 低维分量（小 i）的变化较快，主要捕捉局部位置关系
• 高维分量（大 i）的变化较慢，可以用于编码全局信息

这个怎么去理解？我们把某个位置的向量大概划分为两部分：低维向量部分 + 高维向量部分，低纬向量部分数值波动幅度很大，在一个周期内只能包含少量相邻的位置，并且一定程度上也表达了位置的局部的相对信息，这就是捕捉局部位置关系。那么，对于高纬向量部分而言，它的波动幅度很小，一个周期能够包含更多的位置信息，这也是我们理解的编码全局位置信息的含义。

所以，对于一个基于正弦余弦编码的位置向量，可以理解为该向量中隐含了一些局部和全局的位置信息。使得 Transformer 既能感知局部相对位置，也能感知全局位置信息，从而弥补其原生结构中缺少位置感知能力的缺陷。

当然，这种位置编码方法也存在以下一些不足之处：

随着序列长度的增加，位置编码的周期性可能导致不同位置之间的区分度逐渐降低，难以准确表示极长序列中各个位置的独特信息。

虽然正弦余弦位置编码能够隐含地表达一定的局部位置信息，但由于它是固定的、不可学习的，并没有专门针对局部依赖关系进行优化，因此在建模局部依赖关系时能力相对不足。

正弦余弦位置编码是一种基于三角函数的固定编码方式，它是一种静态的位置信息表示。而注意力机制更关注的是文本中不同位置之间的动态语义关联。这两种信息在表示形式和语义侧重点上存在差异，导致在融合时可能无法很好地相互补充。

正弦余弦位置编码通常是高维向量，其计算量会随着维度的增加不仅需要更多的计算时间，还可能占用大量的内存空间，影响模型的运行效率。

2. 基于可学习的嵌入

可学习的位置编码（Learnable Positional Encoding, LPE）是一种通过梯度下降自动学习位置编码的方法，不同于固定编码（如正弦/余弦函数编码），它不依赖任何手工设计的公式，而是直接让模型在训练过程中优化位置信息。对于一个长度为 \( L \) 的输入序列，每个位置 \( i \) 都对应一个可学习的向量。当训练或测试时，将输入 Token 的编码和对应位置的可学习位置编码向量相加，从而赋予 Token 相应的位置信息。

import torch.nn as nn
import torch


class LearnablePositionalEncoding(nn.Module):
    def __init__(self, max_len, d_model):
        super(LearnablePositionalEncoding, self).__init__()
        # 创建 max_len 个可学习的位置编码
        self.pe = nn.Embedding(max_len, d_model)

    def forward(self, inputs):
        # 生成位置索引
        positions = torch.arange(0, inputs.size(1))
        # 获取对应的可学习位置编码
        return self.pe(positions)


def demo():
    # 示例：假设最大序列长度为 100，隐藏维度为 512
    LPE = LearnablePositionalEncoding(100, 512)
    # (batch_size, seq_len, d_model) => (32, 50, 512)
    inputs = torch.randn(32, 50, 512)
    # 获取可学习的位置编码
    pe = LPE(inputs)
    print(pe.shape)


if __name__ == '__main__':
    demo()

这种位置编码方式能够根据具体的任务和数据特点，模型可以学习到更适合该类文本的位置表示方式，捕捉文本中位置相关的语义和结构信息，这是固定的位置编码（例如：正弦余弦位置编码）难以做到的。但是也存在一些不足之处，例如：

• 如果训练时 max_len=512，测试时输入 1024 长度的序列，模型就无法处理了
• 需要存储 max_len×d_model 维度的参数，可能导致大模型训练更难收敛

至此，我们简单剖析了两种常见的绝对位置编码方法，它们在实际应用中各具优势，同时也存在一定的局限性。随着大模型技术的发展，要求能够支持更长的输入序列，这不仅要求模型具备更强的能力来捕捉复杂位置信息（局部与全局），也对计算效率提出了更高要求。在此背景下，位置编码方法也在不断创新与演进中。