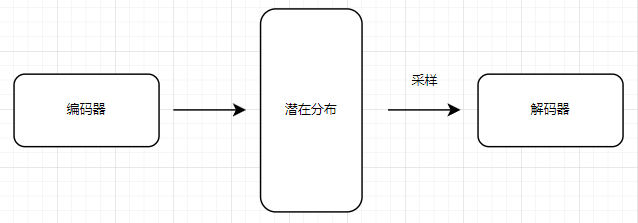
变分自编码器（VAE）是一种深度生成模型。它主要由 编码器（Encoder） 和 解码器（Decoder） 两部分组成：

• 编码器（Encoder）：负责将输入数据 \( x \) 映射到一个 概率分布，即潜在变量 \( z \) 的均值 \( \mu \) 和方差 \( \sigma^2 \)。
• 解码器（Decoder）：通过采样得到的潜在变量 \( z \)，重建输入数据 \( x \) 。

1. 基本思想

假设模型想要知道如何生成一张图像，首先得知道该图像的分布，例如：图像由 4 个像素组成，那么模型得知道这 4 个像素的分布是什么样的，像素之间的关系和依赖是什么，就可以从这分布中采样 4 个像素就可以生成一样图像。

然而，由于图像本身是一个高维的数据，像素的分布和关系是非常复杂的，我们无法直接去描述图像的分布。所以，我们就引入了潜在变量这个概念，其意图是，将高维的复杂的图像数据压缩成一个潜在变量（包含图像的核心信息），我们研究这个潜在变量的分布，这个问题就简单很多了。

生成图像的的时候，由于知道潜在变量的分布，我们就可以从该空间进行采样，然后恢复成一张图像了所以，VAE 的思路就是：

• 首先，将输入图像压缩成一个潜在向量。通常是通过编码器网络来实现的。
• 然后，估计这个潜在向量的分布。VAE 通常会认为潜在空间的分布是一个高斯分布。会去估计这些潜在向量的均值和方差，这样可以定义出潜在空间的分布。
• 接着，当我们想要想要生成图像的时候，就从估计的潜在分布中采样，得到一个潜在向量。
• 最后，根据这个潜在的向量恢复成图像。通常是由解码器（一个神经网络）将潜在向量恢复成图像。

VAE 叫做变分自编码器，这个 “变分” 怎么理解？

变分 在这里指的是 变分推断（Variational Inference, VI），它是一种近似概率分布、简化分布表示的方法。在 VAE 里，我们想让模型学会如何用一个分布来表示图像数据。但是，图像是高维的，像素之间关系复杂，直接对图像分布进行建模非常困难。

所以，我们换个思路——先把图像压缩成一个低维的潜在向量（latent vector），然后只需要研究这个潜在向量的分布，而不需要直接建模整个高维图像数据的分布。这样，问题就变得更简单了。

但新问题又来了：这个潜在向量的真实分布是未知的，我们没法直接求出它。我们通过一些方法，让图像压缩后得到的潜在变量分布尽可能接近我们假设的正态分布。

所以，变分可以理解为就是一种将复杂的分布变换到简单分布上，从而更好解决问题的方法。

2. 损失函数

VAE 的损失函数由两个部分组成：重构损失 和 KL 散度，其中：

• 重构损失：这部分用来度量解码器通过潜在变量 \( z \) 生成的图像和原始输入图像 \( \hat{x} \) x之间的差异。
• KL 散度：VAE 通常假设潜在变量 \( z \) 服从标准正态分布，所以这部分度量由编码器学习到的潜在分布与标准正态分布之间的差异。

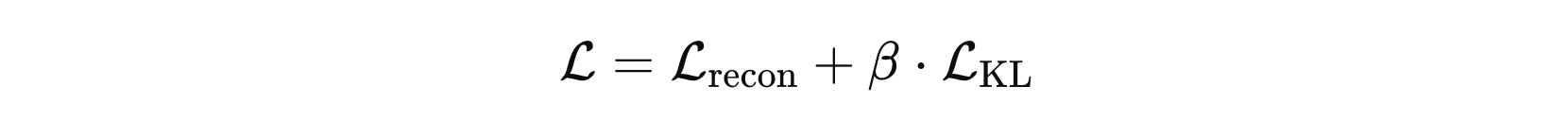
公式中，第一项是重构损失，第二项则是 KLD 损失。重构损失一般用 均方误差 或 二元交叉熵 损失函数。KLD 损失则经过推导之后如下：

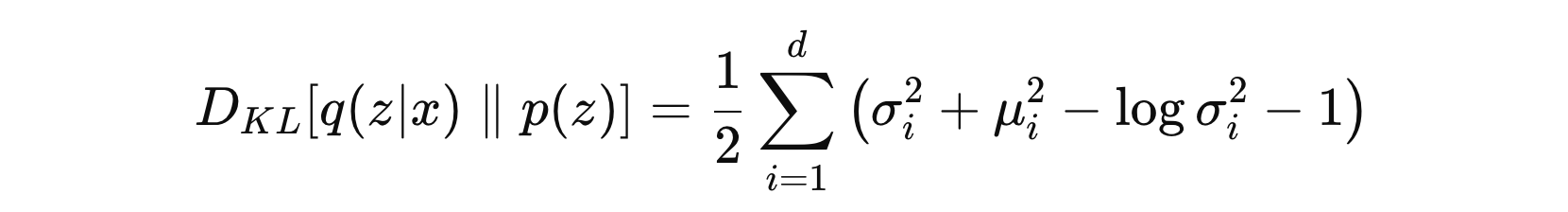
• \( μ_{i} \)​ 是潜在变量的均值
• \( \sigma_i^2 \)​ 是潜在变量的方差

公式中的 \( \beta \) 用于平衡重建损失和 KLD 损失的重要系数，决定了 VAE 更倾向于数据拟合还是强制潜在空间接近标准正态分布。

• \( \beta \) 的增大：增加 KL 散度的权重，使得潜在空间的分布更接近先验分布（通常是标准正态分布）。这将 使潜在空间更加稀疏，更有利于生成任务，因为潜在空间更容易进行 采样，从而生成新的样本。但这样也可能使得重构损失的影响减弱，导致图像重建不够精确。

• \( \beta \) 的减小：减小 KL 散度的权重，让模型 更注重重构损失，从而提高图像重建的精度。这通常对于 图像去噪 和 图像重建 任务更有利，因为这类任务注重 高质量的重建。但是，这样可能会导致 潜在空间过于复杂，从而使得生成样本的质量降低。

3. 重参数化

在训练过程中，VAE使用了“重参数化技巧”来保证梯度可以反向传播。具体来说，编码器输出的均值 \( \mu \) 和标准差 \( \sigma \) 作为正态分布的参数，而潜在变量 \( z \) 通过以下公式从该正态分布中采样：

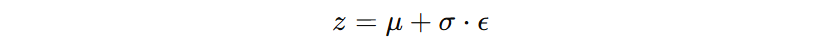
其中，\( \epsilon \) 是来自标准正态分布的随机噪声。这个技巧是VAE能够通过反向传播进行有效训练的关键。

在 VAE 里，我们需要从一个概率分布里“抽签”（采样）来决定潜在变量的值，再交给解码器。但问题是，抽签这个动作是随机的，不是一个可以计算的过程，所以当我们计算损失想要反向传播优化编码器时，梯度就断掉了，没办法回传。

重参数化技巧的解决方案是：别直接抽签，而是先决定分布（均值和标准差），然后再用一个固定的随机因子 \( \epsilon \) 来计算抽签结果。这样，虽然最后的 \( z \) 还是带有随机性，但抽签的方式变成了一个可计算的过程，梯度就能顺利回传，不会卡住。

4. 局限挑战

VAE 在图像生成任务中，通常会生成模糊的图像，其主要原因有：VAE 通常使用均方误差（MSE）或二元交叉熵（BCE）作为重构损失。这类损失函数更倾向于生成平滑的图像，而不是高分辨率的细节。另外，由于 VAE 采用高斯分布进行建模，其生成的图像往往是多个潜在样本的平均值，而不是捕捉到特定样本的细节，导致生成结果模糊。

相比之下，生成对抗网络（GAN）通过判别器来衡量生成图像的真实性，从而能够生成更加锐利、高分辨率的图像。

尽管 VAE 存在这些局限性，但它仍然是一个非常重要的生成模型，特别是在可解释性、潜在空间结构化和稳定训练方面比 GAN 更有优势。