模型量化是指将神经网络模型中的权重和激活值（输入和输出）从高精度的浮点数（例如 32 位浮点数）转换为低精度的整数（如 8 位整数）或更低位数的表示方式。通过这种方式，减少模型的存储需求和计算量。

量化的核心思想是将浮点数值的表示范围映射到更小的整数范围，这个过程涉及两个主要步骤：

根据零点的处理方式，量化分为：

对称量化 (Symmetric Quantization)
在对称量化中，量化后的数值范围是对称的。即正数和负数的量化范围是相同的，零点映射到量化后的零值。对称量化通常使用缩放尺度来量化数据。

非对称量化 (Asymmetric Quantization)
非对称量化后的数值范围不一定对称，量化范围的最小值和最大值可以不同，且不一定是对称的。除了缩放尺度，还需要计算零点来进行量化映射。这种量化方式可以更灵活地适应数据的实际分布，尤其适用于存在偏移的情况。

1. 对称量化

对称量化的特点是量化范围是对称的，通常零点是 0。只需要计算 尺度因子 (S)，没有零点。其缩放尺度的计算公式：

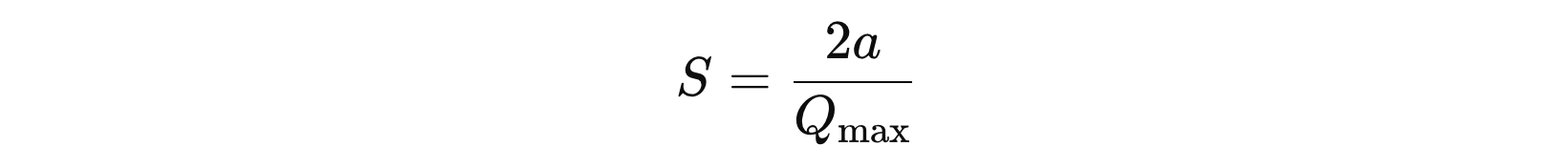
其中：

\( a \) 是原始数据的最大绝对值，即原始数据的范围是 \( [−a,a] \)
\( Q_{max} \) 是量化后的最大整数值，通常为 \( 2^{量化位宽-1} – 1 \)。例如：对于 8 位量化，\( Q_{max} = 127 \)

得到了缩放尺度，可以使用下面的公式进行数值的量化映射：

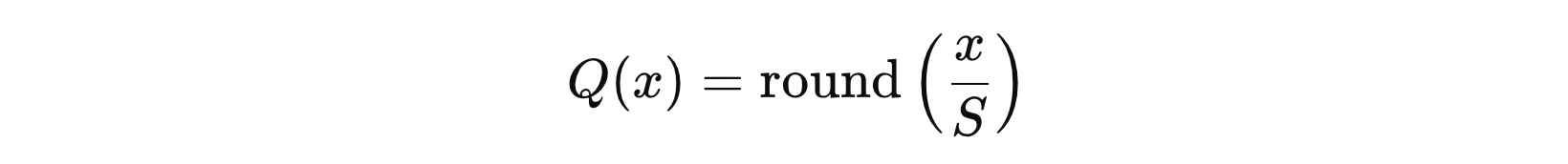
其中，其中，\( x \)是原始值，\( S \) 是尺度因子。

2. 非对称量化

非对称量化的特点是量化范围不对称，零点不为 0。它需要计算 尺度因子 (S) 和 零点 (z)。缩放尺度的计算公式：

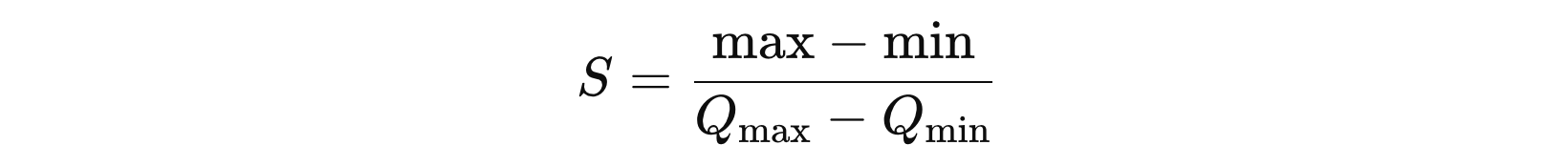
其中：

零点 z 的计算公式：

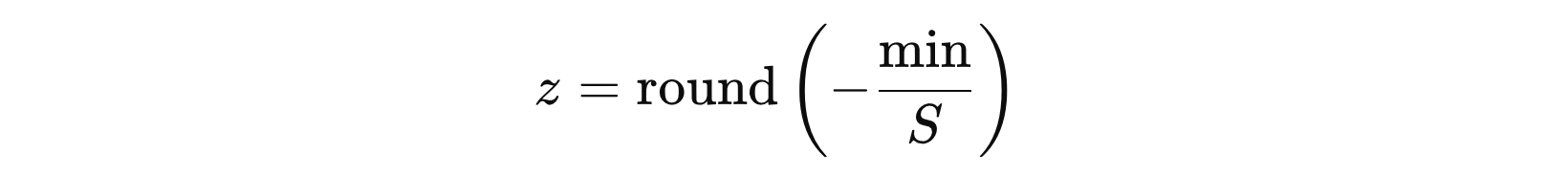
最后，基于缩放因子 S 和零点 z 使用下面公式进行值的量化映射计算：

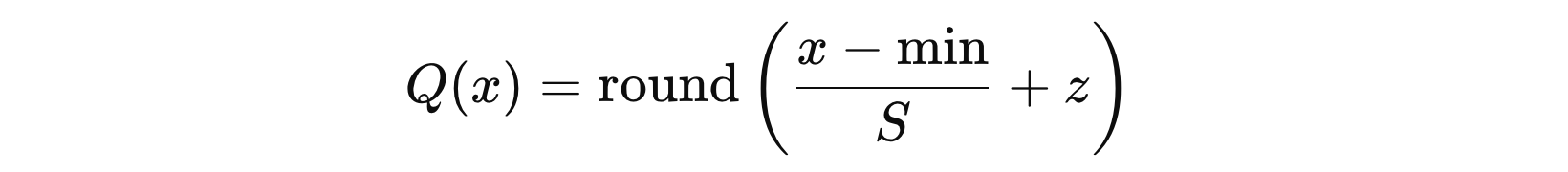
其中，\( x \) 表示输入数据，\( min \) 表示原始数据最小值。

逐层量化（Layer-wise Quantization）：在这种策略下，整个层（layer）的所有权重共享同一组缩放因子S和偏移量Z。它适用于那些各个权重分布相似的情况。
逐组量化（Group-wise Quantization）：在这种策略下，每个权重组（group）有自己的一组缩放因子和偏移量。这种方法在网络中结构化的权重分布较为常见时应用，可以在保证较高压缩率的同时，保持较好的性能。
逐通道量化（Channel-wise Quantization）：在这种策略下，每个通道（channel）的权重都有单独的缩放因子S和偏移量Z。逐通道量化能够提供最精细的量化，通常适用于卷积神经网络（CNN）等有显著通道间差异的结构。

权重量化：目标是减少模型存储需求和计算负载，特别是在推理阶段。量化权重通常能显著减少模型的大小，从而减少存储和传输成本。权重量化通常对每个权重使用固定的缩放因子和偏移量，量化时权重是静态的。

激活值量化：目标是加速推理过程，通过量化激活值来减少计算中的浮点操作，使得推理过程在低精度计算下更加高效。由于激活值会随着输入数据的变化而不同，因此激活值的量化需要输入样本来计算激活值的范围，并基于这些范围来确定量化的参数。

权重量化：在模型训练完成后，权重被量化为低精度整数（比如 int8），并且会为每个权重分配一个对应的缩放因子和零点，用来将它们映射到整数范围。
激活值量化：在推理时，输入数据也会被量化为低精度整数，然后与量化后的权重进行计算。激活值在前向传播中也是以量化后的整数形式进行计算的。
推理过程中的整数运算：推理计算时，计算过程完全是在量化后的整数（如 int8）级别上进行的。中间的计算操作（如加法、乘法等）也是基于整数进行的，不需要反映射到浮点数。
反量化：在推理的最终阶段，输出结果（激活值）可能会被反量化成浮点数（如用缩放因子将整数恢复为浮动精度），以便进行后续的处理或者输出。

简言之：在推理计算过程中，模型是基于量化后的 int8 数据进行计算的，只有在输出阶段，激活值可能会被反量化为浮点数，进行最终结果的输出。

量化过程中可能会引入误差，因为浮点数转换成低精度整数后，可能无法精确表示原始值。因此，量化可能导致模型的性能略微下降，尤其是在精度要求高的应用中。