梯度提升树（GBDT，Gradient Boosting Decision Tree）回归是一种集成学习方法，它通过逐步构建多个决策树来优化预测结果，尤其适用于回归问题。GBDT 通过“加法模型”逐步提高模型的预测能力，每一步都在减少前一步模型的误差。

1. 训练过程

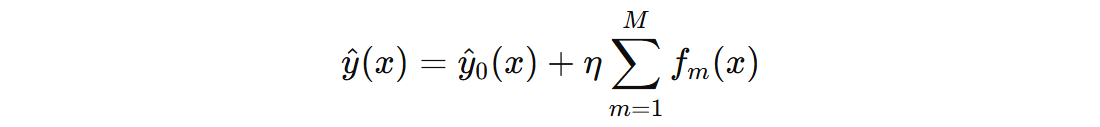
其中：

• \( \hat{y}(x) \) 表示模型对输入 \( x \) 的最终预测值
• \( \hat{y}_{0}(x) \) 表示初识模型，初步的预测值
• \( f_{m}(x) \) 是第 \( m \) 棵树的输出值
• \( \eta \) 表示学习率，控制每棵子树的贡献
• \( M \) 表示 GBDT 中回归决策树的数量

特征1	特征2	特征3	目标值
-0.90802408	1.46564877	-1.4123037	-106.40638687
-0.54438272	-1.15099358	0.11092259	-46.41270092
0.24196227	-1.72491783	-1.91328024	-88.70824211
0.37569802	-0.29169375	-0.60063869	-4.29054154
1.52302986	-0.23413696	-0.23415337	91.04704754
0.54256004	-0.46572975	-0.46341769	11.04262105
0.49671415	0.64768854	-0.1382643	35.80536172
-0.56228753	0.31424733	-1.01283112	-79.21856515
1.57921282	-0.46947439	0.76743473	136.10440487
-0.2257763	-1.42474819	0.0675282	-29.86346474

1.1 初始模型

GBDT 的初始模型 \( \hat{y}_{0}(x) \) 作用是在训练开始时，为每个样本提供一个基础的预测值，后续每棵子树都在此基础上，通过拟合当前残差（或负梯度）来进一步优化预测结果。

注意：初始模型 \( \hat{y}_{0}(x) \) 的输出通常是一个常数（即对所有样本预测同一个值）

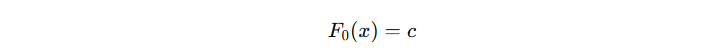
那么，这个初始模型的输出值 c 怎么确定？对于回归预测问题，我们一般使用的 squared error 损失函数，其公式如下：

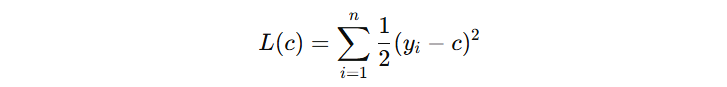
对于初始模型来讲，看看 c 输出什么时，损失函数最小。我们对 c 求导，设导数为 0：

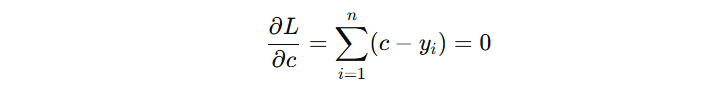
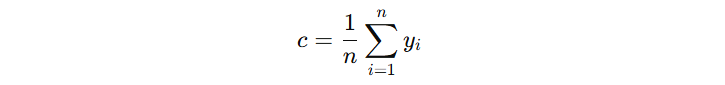
由此可得，初始模型的输出结果为：-8.09005

1.2 子决策树

在 GBDT 中，前面所有子模型（通常是决策树）组合起来，形成当前整体模型的输出，接下来第 m 棵树的目标是：学习如何在当前模型的基础上，进一步降低整体损失函数 L。

特征1	特征2	特征3	目标值	预测值	负梯度
-0.90802408	1.46564877	-1.4123037	-106.40638687	-8.09005	-98.31634
-0.54438272	-1.15099358	0.11092259	-46.41270092	-8.09005	-38.32265
0.24196227	-1.72491783	-1.91328024	-88.70824211	-8.09005	-80.61820
0.37569802	-0.29169375	-0.60063869	-4.29054154	-8.09005	3.79951
1.52302986	-0.23413696	-0.23415337	91.04704754	-8.09005	99.13709
0.54256004	-0.46572975	-0.46341769	11.04262105	-8.09005	19.13267
0.49671415	0.64768854	-0.1382643	35.80536172	-8.09005	43.89541
-0.56228753	0.31424733	-1.01283112	-79.21856515	-8.09005	-71.12852
1.57921282	-0.46947439	0.76743473	136.10440487	-8.09005	144.19445
-0.2257763	-1.42474819	0.0675282	-29.86346474	-8.09005	-21.77342

GBDT 拟合的时候，会把 负梯度当作这一步的目标值。为什么？因为负梯度就是告诉模型，现在我的预测差在哪里，怎么改才能让损失更小。决策树就按照这个方向去分裂、去学习。

想象你在修一座花园的小路。第一遍铺的时候（初始模型），大致铺好，但路面不够平整，有很多坑和高低不平的地方（预测误差）。接下来，每一遍修路（每棵树），你不会重新铺整个路，而是专门针对坑和高处去修，负梯度就像是告诉你哪里需要修。

接下来，以负梯度作为目标值，构建决策树。

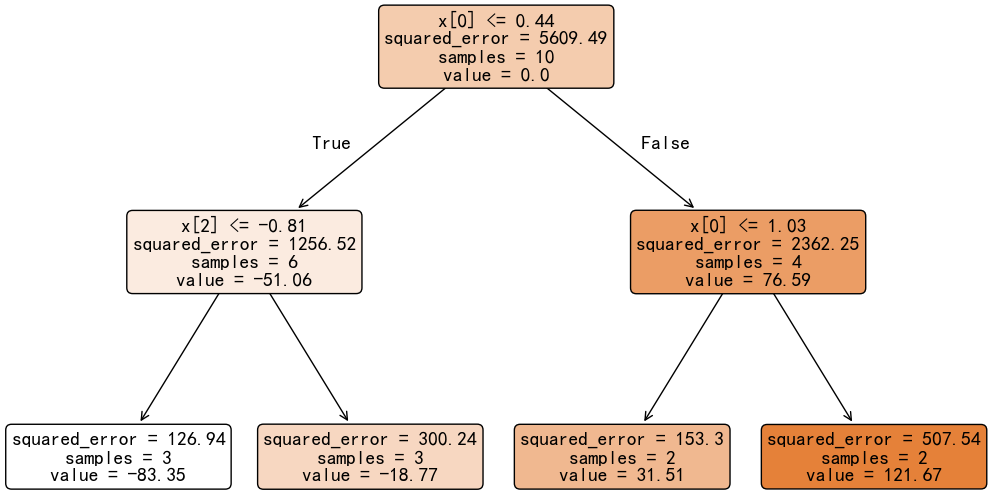
我们在用负梯度训练决策树时，叶子节点输出的其实是 往哪个方向去修正，也就是一种调整方向。它并不是最终的预测值，最终的输出还需要通过叶子节点修正公式来确定。

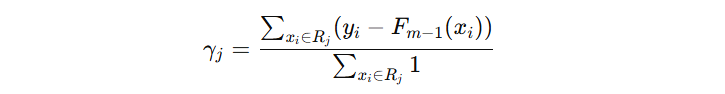
对于 squared_error 损失函数，叶子节点不需要修正，因为修正的公式正好和叶子节点所有样本均值等价。

接下来，继续构建第二棵树：

特征1	特征2	特征3	目标值	初始输出	当前输出	预测输出	负梯度
-0.908024	1.465648	-1.41230	-106.406	-8.09	-83.35	-16.42	-89.98
-0.544382	-1.150993	0.110922	-46.4127	-8.09	-18.77	-9.97	-36.45
0.241962	-1.724917	-1.913280	-88.7082	-8.09	-83.35	-16.43	-72.28
0.375698	-0.291693	-0.600638	-4.29054	-8.09	-18.77	-9.97	5.68
1.523029	-0.234136	-0.234153	91.0470	-8.09	121.67	4.08	86.97
0.5425600	-0.465729	-0.463417	11.04262	-8.09	31.51	-4.94	15.98
0.4967141	0.647688	-0.13826	35.80536	-8.09	31.51	-4.94	40.74
-0.562287	0.3142473	-1.012831	-79.21856	-8.09	-83.35	-16.43	-62.79
1.5792128	-0.469474	0.767434	136.1044	-8.09	121.67	4.08	132.03
-0.22577	-1.424748	0.0675282	-29.8634	-8.09	-18.77	-9.97	-19.90

注意：预测输出 = 初始输出 + 子树输出 * 学习率 。

学习率是用来控制每棵树对最终预测结果的贡献程度，从而能够避免某些性能不佳的子树，导致对预测的结果产生太大的影响。

接下来，基于当前得到的负梯度构建第二棵子树：

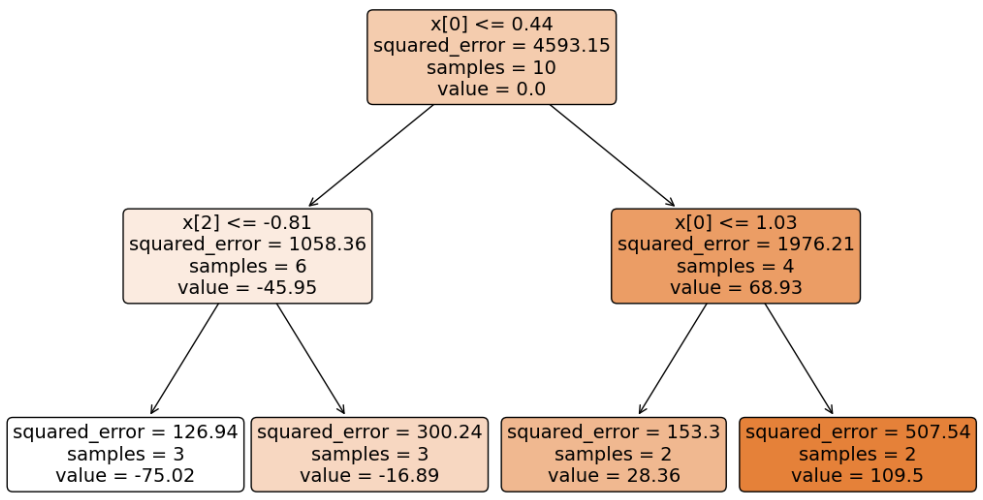
以此类推… 构建出指定数量的子树，完整 GBDT 的训练。

2. 预测过程

假设：我们基于训练数据得到 GBDT 分类模型。这个模型包括一个初始输出模型 + 三棵决策树。

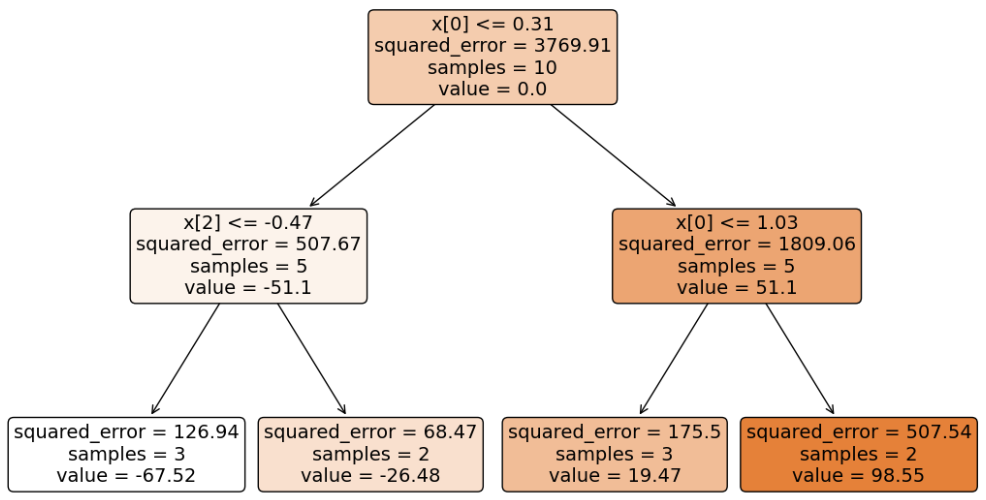
现在基于这个模型，对新数据 [0.64768854, -0.1382643, 0.49671415] 进行预测：
计算该样本的初始分数：-8.09005

• 第一个决策树输出值：31.51
• 第二个决策树输出值：28.36
• 第三个决策树输出值：19.47

假设学习率为 0.1，则最终输出值：-8.09005 + (31.51 + 28.36 + 19.47) * 0.1 = -0.155。

from sklearn.ensemble import GradientBoostingRegressor
from sklearn.datasets import make_regression
import matplotlib.pyplot as plt
from sklearn.tree import plot_tree
import numpy as np


def demo():
    np.random.seed(0)
    x, y = make_regression(n_samples=10, n_features=3, random_state=42)
    gbdt = GradientBoostingRegressor(n_estimators=3, max_depth=2, criterion='squared_error', loss='squared_error')
    gbdt.fit(x, y)

    # 可视化
    # for estimator in gbdt.estimators_:
    #     plt.figure(figsize=(10, 10))
    #     plot_tree(estimator[0], filled=True, rounded=True, fontsize=14, precision=2)
    #     plt.show()

    # 新数据预测
    new_x, new_y = make_regression(n_samples=1, n_features=3, random_state=42)
    print('输入数据:', new_x)

    print('模型计算:', gbdt.predict(new_x)[0])


    # 手动计算
    # 1. 计算初始输出值
    total_score = -8.0900466155

    # 2. 累加每个树输出值
    learning_rate = 0.1
    for estimator in gbdt.estimators_:
        # 每棵树计算得分
        score = estimator[0].predict(new_x)
        # 累加每棵树得分
        total_score += score[0] * learning_rate

    # 3. 最终输出值
    print('手动计算:', total_score)


if __name__ == '__main__':
    demo()

程序输出结果：

输入数据: [[ 0.64768854 -0.1382643   0.49671415]]
模型计算: -0.15512286528967145
手动计算: -0.1551228652868506