GBDT（梯度提升树）不仅能解决回归问题，也同样适用于分类任务。它的核心思想与回归 GBDT 一致：通过不断地迭代修正和逐步优化，使模型在分类场景中持续提升预测性能。

接下来，我们将通过一个具体案例，直观地展示 GBDT 在分类任务中的训练与预测全过程。我们会一步步揭示它的内部机制，看看 GBDT 是如何将多个弱学习器逐层叠加，最终形成一个强大的分类模型，并理解其背后的数学原理。

1. 训练过程

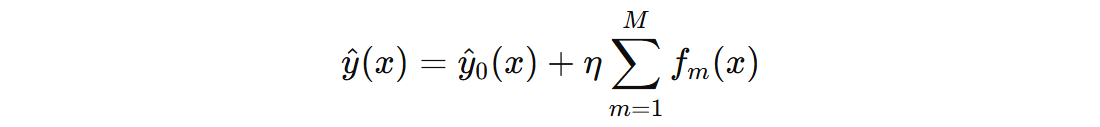
• \( \hat{y}(x) \) 表示模型对输入 \( x \) 的最终预测值
• \( \hat{y}_{0}(x) \) 表示初始输出值
• \( f_{m}(x) \) 表示第 \( m \) 棵树的输出值
• \( \eta \) 表示学习率，控制每棵树的贡献
• \( M \) 表示 GBDT 中回归决策树的数量

特征 1	特征 2	特征 3	标签
-0.587231	-1.971718	-1.057711	0
1.068339	-0.970073	0.208864	1
-1.140215	-0.838792	0.822545	0
-0.077445	-1.599711	-1.220844	0
1.727259	-1.185827	-1.959670	1
-2.895397	1.976862	0.196861	0
-1.962874	-0.992251	-1.328186	0
1.899693	0.834445	0.171368	1
-0.720634	-0.960593	-0.013497	0
-1.715464	2.173706	0.738467	0

1.1 初始模型

GBDT 的初始模型 \( \hat{y}_{0}(x) \) 作用是在训练开始时，为每个样本提供一个基础的预测值，后续每棵子树都在此基础上，通过拟合当前残差（或负梯度）来进一步优化预测结果。

注意：初始模型 \( \hat{y}_{0}(x) \) 的输出通常是一个常数（即对所有样本预测同一个值）

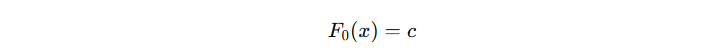
那么，这个初始模型的输出值 c 怎么确定？对于经典的二分类问题，我们一般使用的 log loss 损失函数，其公式如下：

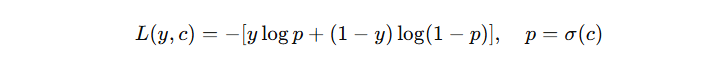
对于初始模型来讲，看看 c 输出什么时，损失函数最小。我们对 c 求导，设导数为 0：

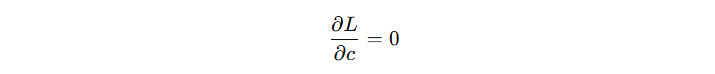
得到初始模型输出计算公式（省略中间推导过程）：

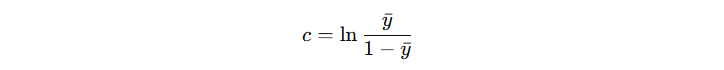
由此可得，初始模型的输出结果为：

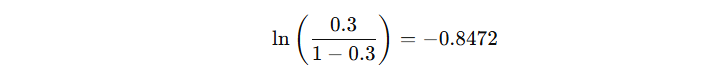
1.2 子决策树

在 GBDT 中，前面所有子模型（通常是决策树）组合起来，形成当前整体模型的输出，接下来第 m 棵树的目标是：学习如何在当前模型的基础上，进一步降低整体损失函数 L。

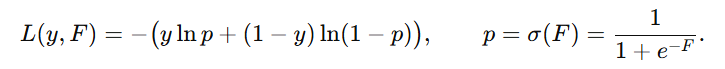
• \( F \) ：模型当前输出值
• \( p \) ：模型预测的概率
• \( y \) ：真实标签（0 或 1）

计算模型的优化方向（负梯度）：

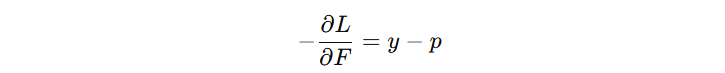
特征 1	特征 2	特征 3	标签	预测分数	预测概率	负梯度
-0.587231	-1.971718	-1.057711	0	-0.8472	0.3	-0.3
1.068339	-0.970073	0.208864	1	-0.8472	0.3	0.7
-1.140215	-0.838792	0.822545	0	-0.8472	0.3	-0.3
-0.077445	-1.599711	-1.220844	0	-0.8472	0.3	-0.3
1.727259	-1.185827	-1.959670	1	-0.8472	0.3	0.7
-2.895397	1.976862	0.196861	0	-0.8472	0.3	-0.3
-1.962874	-0.992251	-1.328186	0	-0.8472	0.3	-0.3
1.899693	0.834445	0.171368	1	-0.8472	0.3	0.7
-0.720634	-0.960593	-0.013497	0	-0.8472	0.3	-0.3
-1.715464	2.173706	0.738467	0	-0.8472	0.3	-0.3

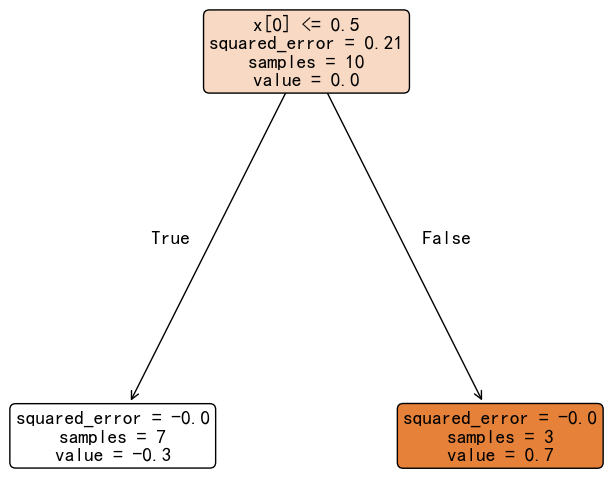
叶子节点的输出值需要进行修正，公式如下：

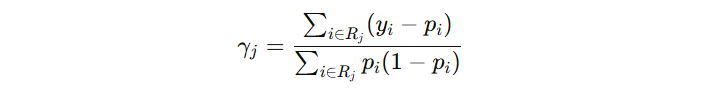
• 左叶子节点（7 个 0 样本）：-0.3 / (0.3 * 0.7) = -1.43
• 右叶子节点（3 个 1 样本）：0.7 / (0.3 * 0.7) = 3.33
  

最终得到第一个子决策树模型：

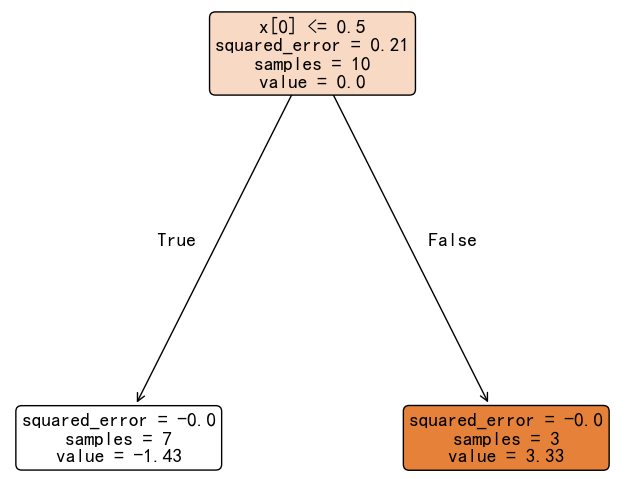
接下来，按照前面的思路继续构建第二棵子决策树：

特征 1	特征 2	特征 3	标签	预测分数	预测概率	负梯度
-0.587231	-1.971718	-1.057711	0	-0.99016	0.27	-0.27
1.068339	-0.970073	0.208864	1	-0.51396	0.37	0.63
-1.140215	-0.838792	0.822545	0	-0.99016	0.27	-0.27
-0.077445	-1.599711	-1.220844	0	-0.99016	0.27	-0.27
1.727259	-1.185827	-1.959670	1	-0.51396	0.37	0.63
-2.895397	1.976862	0.196861	0	-0.99016	0.27	-0.27
-1.962874	-0.992251	-1.328186	0	-0.99016	0.27	-0.27
1.899693	0.834445	0.171368	1	-0.51396	0.37	0.63
-0.720634	-0.960593	-0.013497	0	-0.99016	0.27	-0.27
-1.715464	2.173706	0.738467	0	-0.99016	0.27	-0.27

注意：预测分数 = 初始模型输出分数 + 学习率 * 第一课树输出分数

接下来，创建有一棵新的决策树去拟合负梯度，然后再修正叶子节点输出值。反复执行该动作，直到创建出指定数量的决策树，GBDT 分类模型训练完毕。

from sklearn.ensemble import GradientBoostingClassifier
from sklearn.datasets import make_classification


def demo():
    x, y = make_classification(n_samples=10, n_features=3, n_redundant=0, n_repeated=0, weights=[0.7, 0.3], random_state=42)
    gbdt = GradientBoostingClassifier(n_estimators=3, criterion='squared_error', loss='log_loss')
    gbdt.fit(x, y)


if __name__ == '__main__':
    demo()

2. 预测过程

假设：我们基于训练数据得到 GBDT 分类模型。这个模型包括一个初始输出模型 + 三棵决策树。

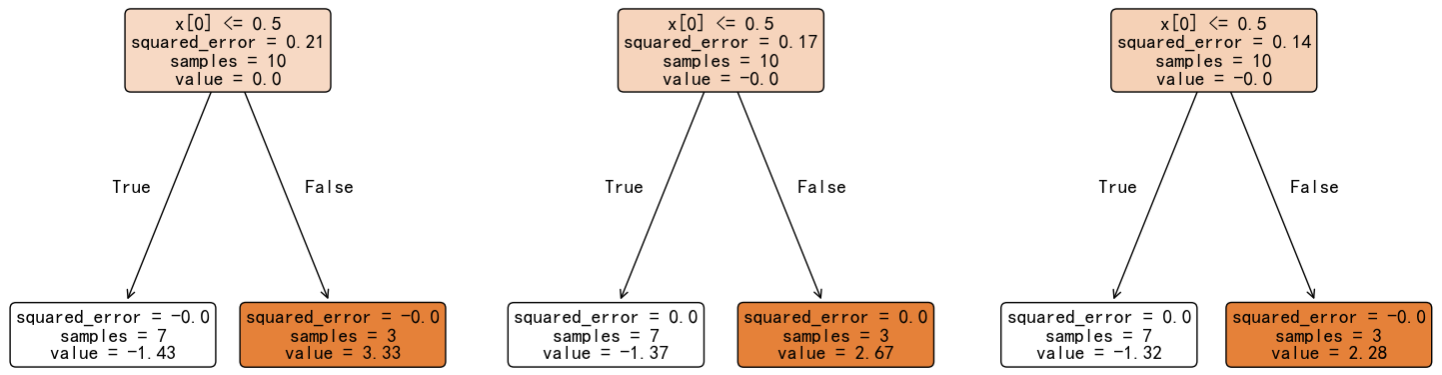
现在基于这个模型，对新数据 [0.49671415 -0.1382643 0.64768854] 的类别进行预测：

首先，计算该样本的初始分数：-0.84729786

然后，我们将新样本输入到每个决策树，分别得到的每个决策树的输出分数：

• 第一棵树：3.33
• 第二棵树：2.67
• 第三棵树：2.28

接着，假设学习率为 0.1，将所有的分数加起来：-0.85 + (3.33+2.67+2.28) * 0.1 = -0.0187849

最后，，使用 sigmoid 函数计算得到该样本属于 1 类别的概率：sigmoid(-0.0187849) = 0.5046

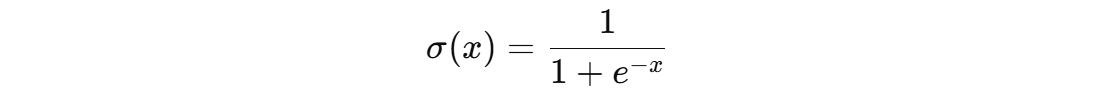
新样本属于 1 类别的概率为：0.5046，属于 0 类别的概率为 0.4954。由于 1 类别概率较高，最终新样本归类到 1 类别。

from sklearn.ensemble import GradientBoostingClassifier
from sklearn.datasets import make_classification
import matplotlib.pyplot as plt
from sklearn.tree import plot_tree
import numpy as np


def demo():
    x, y = make_classification(n_samples=10, n_features=3, n_redundant=0, n_repeated=0, weights=[0.7, 0.3], random_state=42)
    gbdt = GradientBoostingClassifier(n_estimators=3, criterion='squared_error', loss='log_loss')
    gbdt.fit(x, y)

    # 可视化
    # for estimator in gbdt.estimators_:
    #     plt.figure(figsize=(10, 10))
    #     plot_tree(estimator[0], filled=True, rounded=True, fontsize=14, precision=2)
    #     plt.show()

    # 新数据预测
    np.random.seed(42)
    new_x = np.random.randn(1, 3)
    print('未知数据:', new_x)
    print('直接计算类别概率:', gbdt.predict_proba(new_x)[0])


    # 手动计算
    # 1. 初始得分
    total_score = -0.84729786

    # 2. 累加每个树的得分
    learning_rate = 0.1
    for estimator in gbdt.estimators_:
        # 每棵树计算得分
        score = estimator[0].predict(new_x)
        # 累加每棵树得分
        total_score += score[0] * learning_rate

    # 3. 将得分输出概率
    sigmoid = lambda x: 1 / (1 + np.exp(-x))
    proba = sigmoid(total_score)
    print('手动计算类别概率:', np.array([1 - proba, proba]))


if __name__ == '__main__':
    demo()

程序输出结果：

未知数据: [[ 0.49671415 -0.1382643   0.64768854]]
直接计算类别概率: [0.50469609 0.49530391]
手动计算类别概率: [0.50469609 0.49530391]