对偶形式的感知机将权重向量表示为训练样本和对应标记的线性组合，因此不需要显式地维护权重向量，而是通过记录支持向量（误分类的样本）与权重更新系数的乘积来完成分类。

1. 基本原理

感知机原始形式的参数更新规则是：

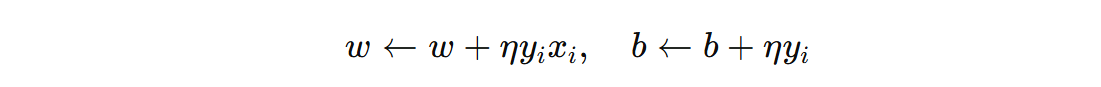
其中 \( \eta \) 是学习率，\(x_{i}\) 是被误分类的样本，\( y_{i}∈\{−1,+1\} \) 是其标签。假设初始的 \(w_{0}=0\)、\(b_{0}=0\)，经过 T 次迭代后，更新结果可以写成：

其中 M 表示所有被误分类并用于更新的样本集合。这说明：

• 权重 \(w\) 是所有误分类样本 \(x_{i}\) 的线性组合
• 偏置 \(b\) 是所有误分类样本标签 \(y_{i}\) 的加权和

既然 \(w\) 是误分类样本的加权和，可以直接假设：

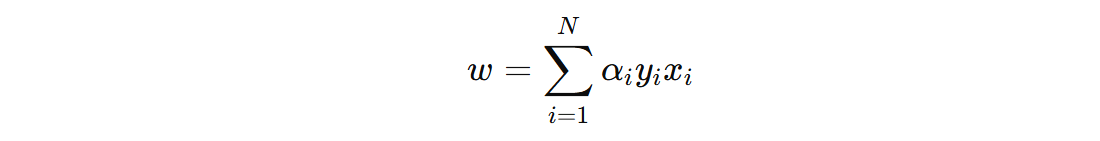
\(α_{i}\)​ 是样本 \(x_{i}\)​ 对 \(w\) 的贡献，具体为误分类后累积的更新次数。对于未被误分类的样本 \(α_{i} = 0\)​。偏置 \(b\) 同样依赖于误分类样本的标签更新：

将 \(w\) 的表示代入感知机的分类函数：

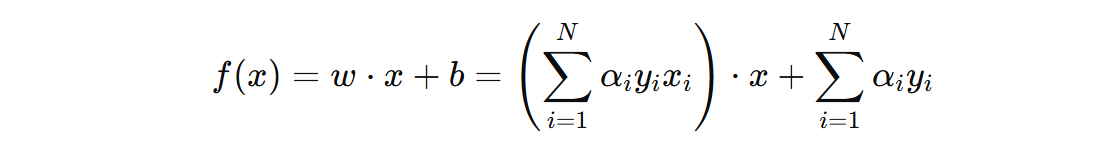
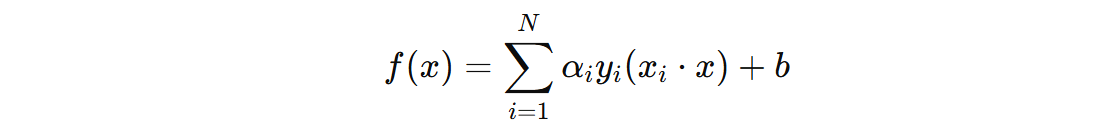
这说明，感知机对偶形式直接通过计算样本之间的内积来做预测，不需要显式地计算每个特征的权重。这就使得在高维数据中，原始形式每次训练都需要计算权重向量和每一个样本的內积（要判断是否预测正确），效率比较低。而对偶形式，则只需要计算部分对偶系数不为 0 的样本的內积。这就能够一定程度上减少计算量。

对于既高维、又稀疏的数据，对偶形式只需要存储少数支持向量（对决策边界有影响的向量），这些向量可以进行优化存储（只存储不为 0 的值）、优化计算（只计算不为 0 的值）。

通常在实际应用中，对偶感知机的参数更新规则可以是：

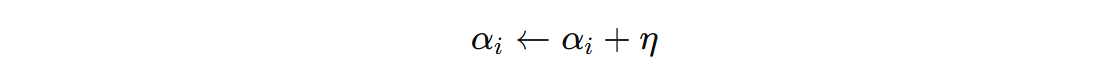
其中 \( \eta \) 是学习率，\(α_{i}\)​ 是对应样本的对偶系数。如果样本 \(x_{i}\)​​ 被误分类（即 \( y_{i}f(x_{i})\leq 0 \)），则更新其对应的对偶系数，然后就可以根据上面的公式计算得出 \(w\) 和 \(b\)。

只有当 \(α_{i} > 0\)​ 时，样本 \(x_{i}\)​​ 才对决策边界有贡献。

2. 应用场景

对偶形式的感知机有以下几个特点：

1. 利用内积计算： 利用样本间的内积计算在训练时更新和分类
2. 适用于核方法： 可以扩展到非线性分类，通过引入核函数替代内积
3. 适合高维稀疏： 高维稀疏场景能够加快训练、预测计算

何时使用对偶形式？

• 当数据非线性可分，且需要结合核函数解决问题。
• 当样本数量不多，但特征维度较高，且需要稀疏计算时。

何时使用原始形式？

• 数据是线性可分的，或只是需要一个简单的线性分类器。
• 样本数量很大，而特征维度相对较低。

需要注意的是：sklearn.linear_model.Perceptron 的实现并不是对偶形式，而是采用了原始形式。也就是说， 使用的是直接更新权重向量 \(w\) 和偏置 \(b\) 的原始感知机算法。

感知机原始算法（Perceptron）