Lasso 回归（Least Absolute Shrinkage and Selection Operator）是一种广泛应用于统计学和机器学习中的回归分析方法。它通过对回归模型中的系数进行约束，能够有效地进行特征选择和正则化，从而提高模型的泛化能力。

Lasso 回归与岭回归类似，都是为了处理过拟合问题，但 Lasso 回归能够通过对系数的 L1 正则化来实现特征选择，从而使得一些特征的系数变为零，最终 丢弃 这些不重要的特征。

1. 目标函数

这句话在表达上确实存在一些不够专业和准确的地方。以下是改进后的表述：

改进后的表述：​

Lasso 回归（Least Absolute Shrinkage and Selection Operator）通过在损失函数中引入 L1 正则化项，对模型参数的绝对值之和施加约束，从而在优化过程中倾向于将某些特征的权重压缩至零。这种特性使得 Lasso 不仅能够有效防止过拟合，还能实现特征选择，生成一个稀疏且解释性更强的模型。

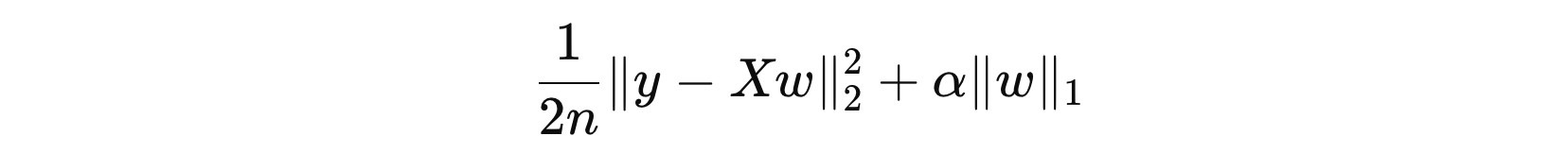
其中：

• \( n \) 表示样本数量
• \( y \) 表示目标变量
• \( X \) 表示特征矩阵
• \( w \) 表示特征权重
• \( α \) 表示正则化系数

然而，Lasso 回归在处理存在多重共线性（multicollinearity）的数据时，可能会表现出一定的局限性。多重共线性是指自变量之间存在高度线性相关性的现象，这会导致回归模型参数估计的方差显著增大，进而降低估计的稳定性和精度。尽管 Lasso 回归通过 L1 正则化能够产生稀疏解并实现特征选择，但在多重共线性较强的情况下，它可能无法有效地处理变量之间的相关性，从而导致选择的特征和估计的系数不够稳定。此外，Lasso 回归的系数估计本身是有偏的，尤其在正则化强度较大时，这种偏差可能会进一步放大。

2. 算法使用

from sklearn.linear_model import Lasso
from sklearn.datasets import make_regression

def demo():
    # 构建数据
    X, y = make_regression(n_samples=100, n_features=5, noise=0.1, random_state=42)

    # 参数求解
    alphas = [0.1, 1, 10, 50]
    for alpha in alphas:
        estimator = Lasso(alpha=alpha)
        estimator.fit(X, y)
        print('%.2f\t' % alpha, estimator.coef_)


if __name__ == '__main__':
    demo()

0.10	 [60.49530393 98.53560456 64.39154364 56.94764267 35.53084538]
1.00	 [59.64279471 97.46654743 62.88477177 55.96346629 34.82323255]
10.00	 [51.11770255 86.77597616 47.81705308 46.12170248 27.7471042 ]
50.00	 [14.9661717  40.93641389  0.          4.61889541  0.        ]

在 scikit-learn 中，Lasso 回归的正则化系数 α（alpha）是一个非负值（即 α ∈ [0, ∞]）。α 的值越大，对模型权重的惩罚力度越大，导致权重的值越小，甚至等于 0。这有助于防止过拟合，还能实现特征选择，生成一个稀疏且解释性更强的模型。