高斯混合模型（Gaussian Mixture Model，GMM）是一种基于概率的无监督学习模型，通过假设数据由多个高斯分布组成来进行数据建模，在机器学习、统计学和信号处理等领域有广泛的应用。

1. 基本理解

假设：我们要分析一组组学生的期末考试成绩。经过分析，你发现这些学生的成绩大多数集中在一个范围内，比如大部分学生的成绩在 60 到 90 分之间，并且成绩都集中在平均分附近，离平均分越远的学生越少。在这种情况下，我们可以使用 一个高斯分布 来很好地描述这组数据，因为数据的分布简单且集中在一个中心区域。

如果我们分析公司不同部门员工的薪资，由于公司里有不同的员工等级，薪资也是不同的：

• 初级员工：薪资大多在 3000 到 5000 元之间，比较低。
• 中级员工：薪资大多在 5000 到 8000 元之间，适中。
• 高级员工：薪资大多在 8000 到 12000 元之间，较高。

这些不同等级的员工薪资数据分布各自有自己的规律，并且它们之间有明显的差异。因此，单一的高斯分布无法准确描述所有员工的薪资数据。

在这种情况下，我们可以使用 多个高斯分布 来描述这些数据。每个高斯分布代表一个薪资群体（如初级、中级和高级员工），这些高斯分布加在一起就能更好地描述整个公司的薪资分布情况。

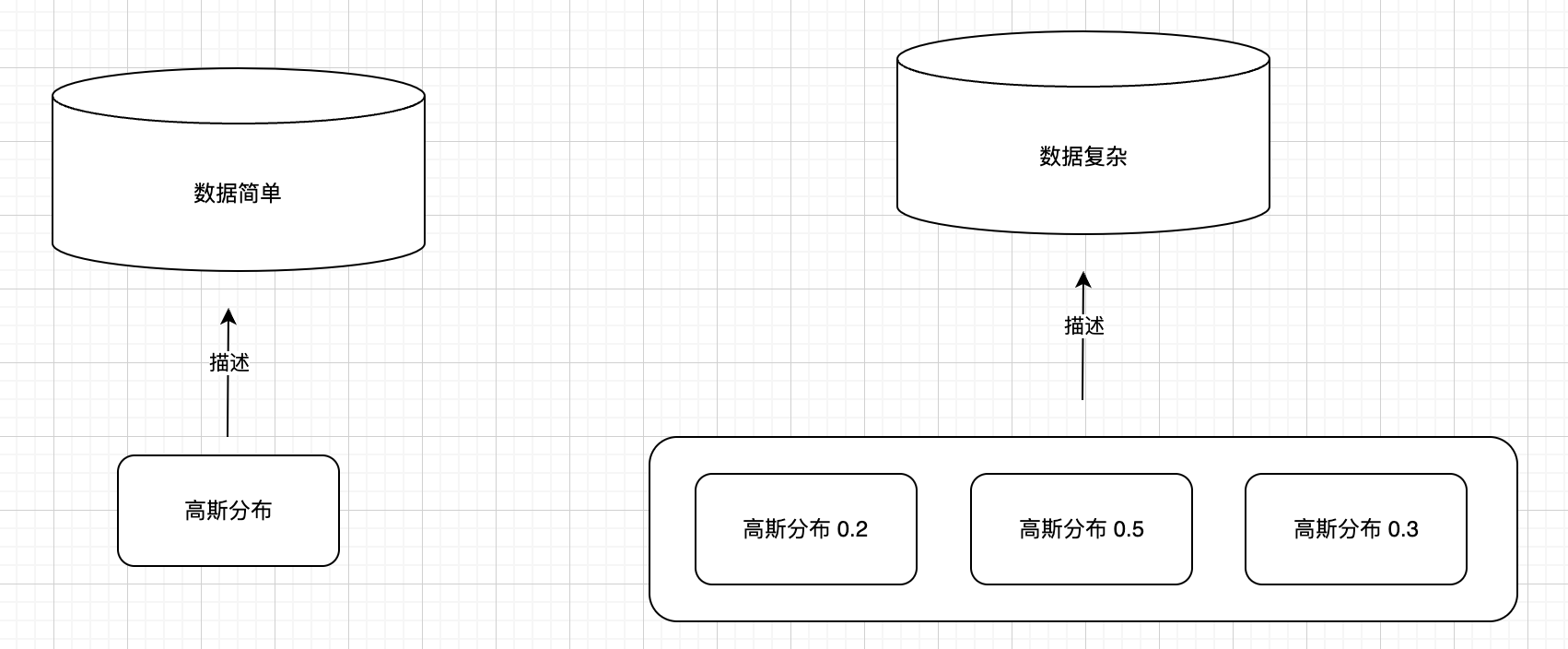
• 如果数据的分布简单，那么使用一个高斯分布就可以表示该数据；
• 如果数据的分布复杂，那么可以使用多个高斯分布来表示该数据。

将多个高斯分布组合到一起，来表示数据分布的模型，叫做高斯混合模型。

• 从整体来看：GMM 能够建立对复杂数据分布的表示，那么，我们就可以使用高斯混合模型来产生满足该分布的数据，可应用于数据增强。
• 从细节来看：GMM 由多个高斯分布组合而成，每一个高斯分布又可以理解为一类数据，可应用于数据聚类。

2. 代码示例

import matplotlib.pyplot as plt
from sklearn.mixture import GaussianMixture
from sklearn.datasets import make_blobs
import numpy as np


def test():

    # 创建数据
    np.random.seed(0)
    x, y = make_blobs(n_samples=1000,
                      n_features=2,
                      centers=[(0, 1.5), [1, 0.5]],
                      cluster_std=[0.4, 0.5],
                      random_state=42)

    # 模型训练
    estimator = GaussianMixture(n_components=2, random_state=42)
    estimator.fit(x)

    # 1. 用于数据聚类
    y_pred = estimator.predict(x)
    print(y_pred)

    # 2. 用于产生数据
    data = estimator.sample(3)
    print(data)

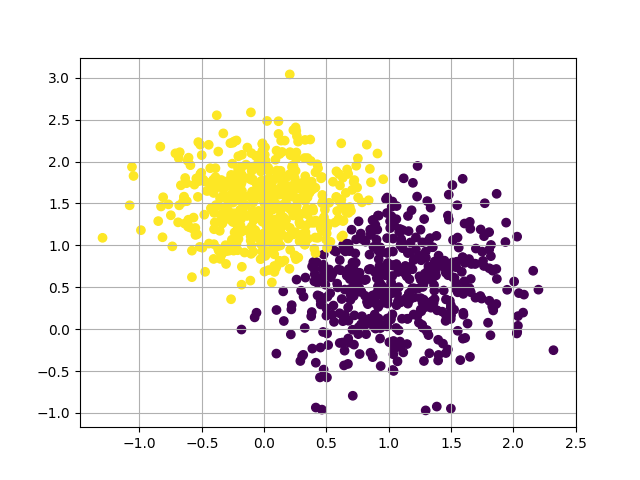
    # 可视化
    plt.grid()
    plt.scatter(x[:, 0], x[:, 1], c=y_pred)
    plt.show()


if __name__ == '__main__':
    test()