激活函数主要用来向神经网络中加入非线性因素,以解决线性模型表达能力不足的问题,它对神经网络有着极其重要的作用。我们的网络参数在更新时,使用的反向传播算法(BP),这就要求我们的激活函数必须可微。sigmoid 激活函数在早期的神经网络中经常使用,目前已经逐渐被其他激活函数取代。
1. sigmoid 激活函数
sigmoid 函数公式:
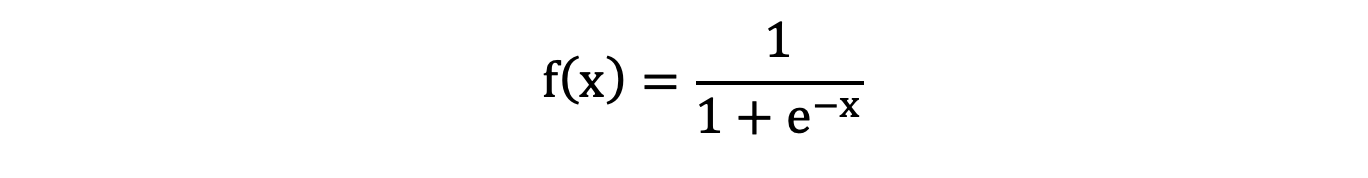
import torch
import matplotlib.pyplot as plt
import torch.nn.functional as F
def test():
_, axes = plt.subplots(1, 2)
# 函数图像
x = torch.linspace(-20, 20, 1000)
y = F.tanh(x)
axes[0].plot(x, y)
axes[0].grid()
axes[0].set_title('Sigmoid 函数图像')
# 导数图像
x = torch.linspace(-20, 20, 1000, requires_grad=True)
torch.sigmoid(x).sum().backward()
axes[1].plot(x.detach(), x.grad)
axes[1].grid()
axes[1].set_title('Sigmoid 导数图像')
plt.show()
if __name__ == '__main__':
test()
函数图像如下:
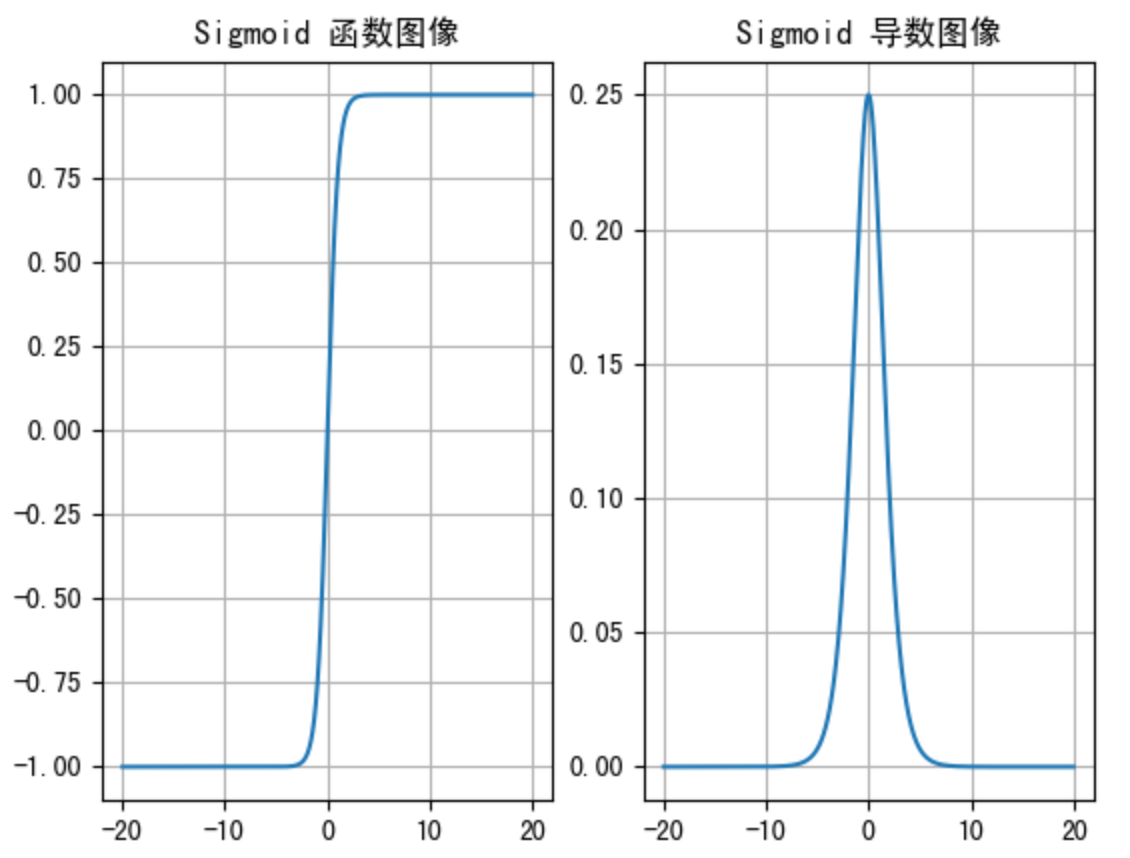
从 sigmoid 函数图像可以得到,sigmoid 函数可以将任意的输入映射到 (0, 1) 之间,当输入的值大致在 <-6 或者 >6 时,意味着输入任何值得到的激活值都是差不多的,这样会丢失部分的信息。比如:输入 100 和输出 10000 经过 sigmoid 的激活值几乎都是等于 1 的,但是输入的数据之间相差 100 倍的信息就丢失了。
对于 sigmoid 函数而言,输入值在 [-6, 6] 之间输出值才会有明显差异,输入值在 [-3, 3] 之间才会有比较好的效果。
通过上述导数图像,我们发现导数数值范围是 (0, 0.25),当输入 <-6 或者 >6 时,sigmoid 激活函数图像的导数接近为 0,此时网络参数将更新极其缓慢,或者无法更新。
2. logsigmoid 激活函数
sigmoid 激活函数还有一个变种 LogSigmoid,其将输入的数值映射到 (-inf, 0),其公式如下:
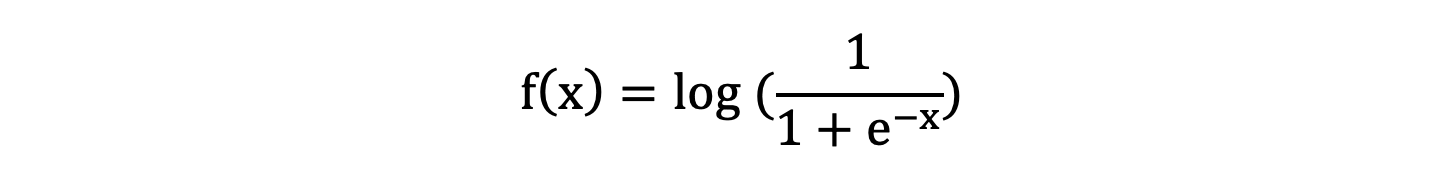
import torch
import matplotlib.pyplot as plt
import torch.nn.functional as F
# 绘制图像
def draw(x, y):
plt.plot(x, y)
plt.grid()
plt.show()
def test():
# 函数图像
x = torch.linspace(-20, 20, 1000)
y = F.logsigmoid(x)
draw(x, y)
if __name__ == '__main__':
test()
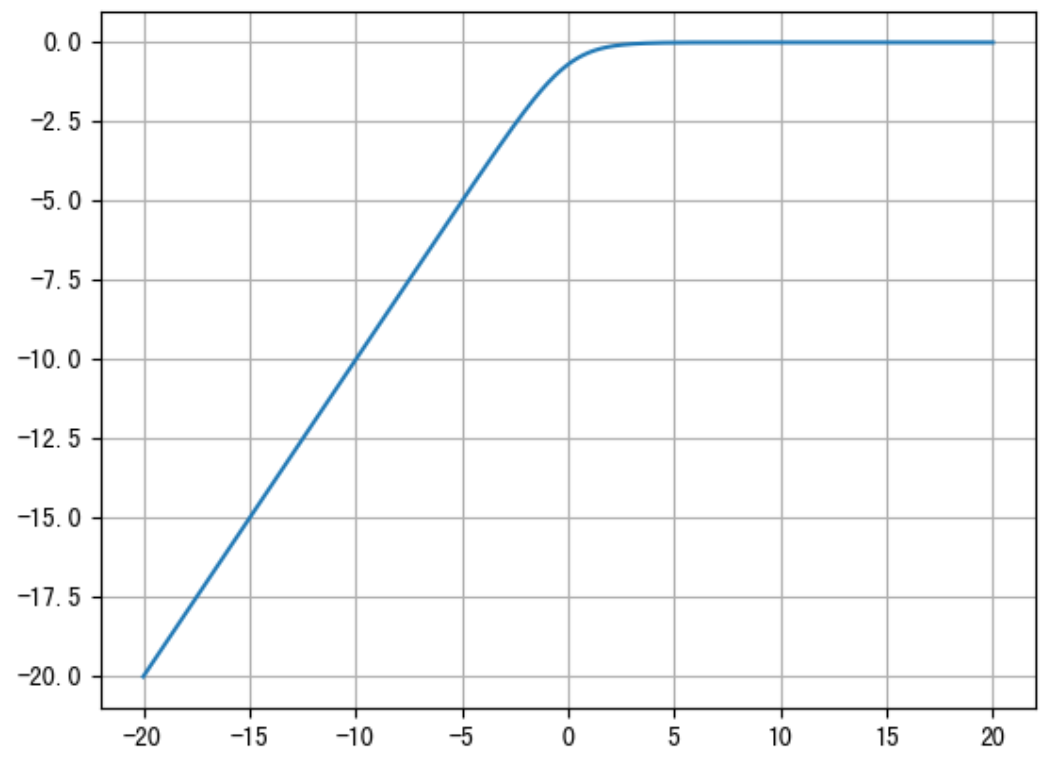
函数图像如下:

 冀公网安备13050302001966号
冀公网安备13050302001966号